利用高精度迎风紧致群速度控制法模拟激波与柱形界面相互作用*

姚清河，陈耀钦，薛 莉，朱庆勇

(中山大学应用力学与工程系，广东 广州 510275)

众所周知，对于气动方程，不管初始值如何光滑，其解都可能出现间断,采用高于一阶精度格式求解激波问题时，其数值解在激波附近都会产生非物理振荡。

在流场激波捕捉技术中，已经发展了许多行之有效的方法，如TVD 格式、ENO 格式、WENO 格式、CSCM格式、NND 格式、耗散比拟方法等[1-7],这些格式都有较高的精度和激波分辨率。群速度控制法从物理角度出发分析非物理振荡产生原因[8-9]，并提出改进激波解的办法。在这个思想基础上，本文从五阶迎风紧致格式出发，引进一个函数用以控制数值解的群速度，构造带有群速度控制的五阶迎风紧致格式。该格式在激波前后表现为不同的性质，使得激波前后的振荡向激波靠拢，从而达到消除激波振荡的目的。同时，文中进一步对所构造的格式的精度及数值解的行为进行了分析。

对于接触间断两边的流体，一方面以上格式始终存在数值耗散而导致接触间断被抹平，另一方面Euler 方法在模拟时需要进行特别的处理，如MAC，VOF和Level Set法等。本文在前人基础上，采用五阶迎风紧致格式求解描述界面的Level Set 方程，采用Ghost法处理界面附近的边界条件[10]。本方法在激波与柱形界面相互作用的计算中取得良好的结果，数值结果与实验是吻合的。

1 控制方程

1.1 流场控制方程

针对激波与流体界面相互作用的问题，由欧拉坐标系中二维非定常可压缩守恒性Euler 方程来描述流场。具体地

(1)

其中

,,

流体的状态方程为

p=(γ-1)(E-ρ/2(u2+v2))

其中，ρ是密度，u,v分别是x,y方向上的速度分量，p是流体压力，E是单位体积流体的总能量，e是比内能。

1.2 Level Set 方程

二维界面Level Set方程

φt+uφx+vφy=0

(2)

其中，φ(x,t)是x到界面Γ(t)的符号距离，u=(u,v)是流体速度，t是时间。但是，由于数值方法的内在效应，即使只进行了几个时间步求解，φ(x,t)将不再满足符号距离函数的定义了。为了保持这一良好性质，我们采用一种所谓重新初始化(Reinitialization)的手段[11]，也就是要改造φ(x,t)使重新成为x到界面Γ(t)的符号距离。重新初始化方程如下

(3)

2 数值方法

2.1 标量方程的空间离散方法

首先考虑如下的模型方程及对应的半离散化方程

,f=cu,c=const

(4)

(5)

这里Fj/Δx是一阶导数∂f/∂x的差分逼近。考虑取如下五个网格点相联系的差分逼近[11]

ω1Fj+1+ω0Fj+ω-1Fj-1=β-2fj-2+β-1fj-1+

β0fj+β1fj+1+β2fj+2

(6)

,,，

这样(6)式可写为

(7)

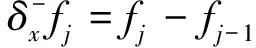
Δx5)

(8)

即逼近精度的量级为Δx5。

简单采用(7)式,该方法经过激波时存在非物理振荡。本文采用如下群速度控制方法以克服激波附近非物理振荡，提高激波分辨率，同时提高了光滑区的计算精度。本文在(5)式右端加入修正项以控制其群速度。

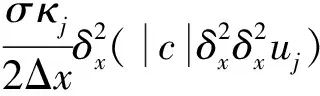
(9)

(10)

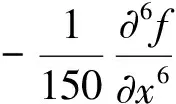
1)情形一，ssj+1=ssj-1=1：

σ(-cos3α+6cos2α-15cosα+10)，

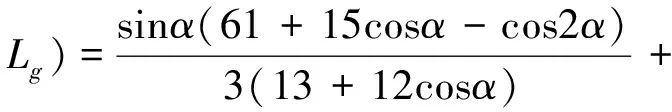
σ(3cos3α-8cos2α+5cosα)

我们有kr≥0,∀α∈[0,π]。D(α)≥1,∀α∈[0,α*]，这里0<α*<π。

2)情形二，ssj+1=1,ssj-1=-1：

σ(2cos2α-8cosα+6)，

我们有kr≥0,∀α∈[0,π]。

3)情形三，ssj+1=-1,ssj-1=1：

σ(-2cos3α+10cos2α-22cosα+14)，

我们有kr≥0,∀α∈[0,π]。

4)情形四，ssj+1=-1,ssj-1=-1：

σ(-cos3α+6cos2α-15cosα+10)，

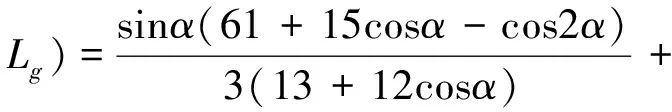
σ(-3cos3α+8cos2α-5cosα)

我们有kr≥0,∀α∈[0,π]。D(α)≤1,∀α∈[0,α*]，这里0<α*<π。

在上述四种情况中，情形一和四的范数ki-αL2大于情形二、三的范数ki-αL2。情形二、三的范数ki-αL2相等。

根据以上分析，我们可以得到以下结论，在情形一中，Lg能使得振荡波向激波靠拢；在情形二、情形三中，Fj+σLg都是正耗散，有利于振荡的消除，Fj的群速度不受影响；情形四中，Lg也能使得振荡波向激波靠拢。

带群速度控制的五阶迎风紧致格式Fj+σLg的色散性质、耗散性质和群速度，分别如图1，图2，图3所示(σ=0.5)。

图1 带群速度控制的五阶迎风紧致格式的色散性质

图2 带群速度控制的五阶迎风紧致格式的耗散性质

图3 带群速度控制的五阶迎风紧致格式的群速度

2.2 二维空间离散方法

在对实际流动问题进行数值模拟时，往往会碰到区域边界形状复杂和物理变量在区域内变化大的情况。这时，为了较好的进行模拟，需要先建立曲线坐标网格，即把不规则物理域先映射到规则计算域，然后才能在计算域上进行差分计算。当然，相应的流体力学方程组也需要变换到计算域。

假设物理域上的(t,x,y)到矩形计算域上的(τ,ξ,η)之间的坐标变换为

(11)

则可以把方程(1)变换成如下方程

(12)

其中

ξxηy-ξyηx，/J，

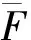
(13)

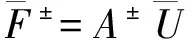
(14)

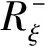
特征值矩阵为

采用Steger-Warming 通量分裂技术

±ε2)1/2)/2],l=1,2,3,4；

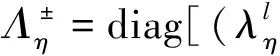
逼近(12)式且具有群速度控制项的半离散差分格式为

(15)

2.3 Level Set方程的离散方法

本文采用五阶迎风紧致格式对二维界面Level Set方程(2)式进行空间离散。重新初始化方程是一个Hamilton-Jacobi方程，方程(3)可以写为如下形式：

φt+H(φx,φy)=0

(16)

方程(16)的半离散形式如下

(17)

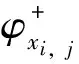
(18)

其中

,,

I(a,b)=[min(a,b),max(a,b)],

(19)

本文利用Ghost方法将Level Set 函数与物理量的控制方程进行耦合，详见文[10]。本文在时间方向采用三阶R-K方法。

3 数值结果

一个Mach数为1.22的激波通过一个气泡相遇，无量纲计算区域(0,325)×(-44.5,44.5)。网格为325×81，无量纲化初值条件是

x>225:ρ=1.374 6,u=-0.394,

v=0,p=1.569 8；

x≤225:ρ=1,u=0,v=0,p=1；

(x-175)2+y2≤252:ρ=3.153 8,

u=0,v=0,p=1

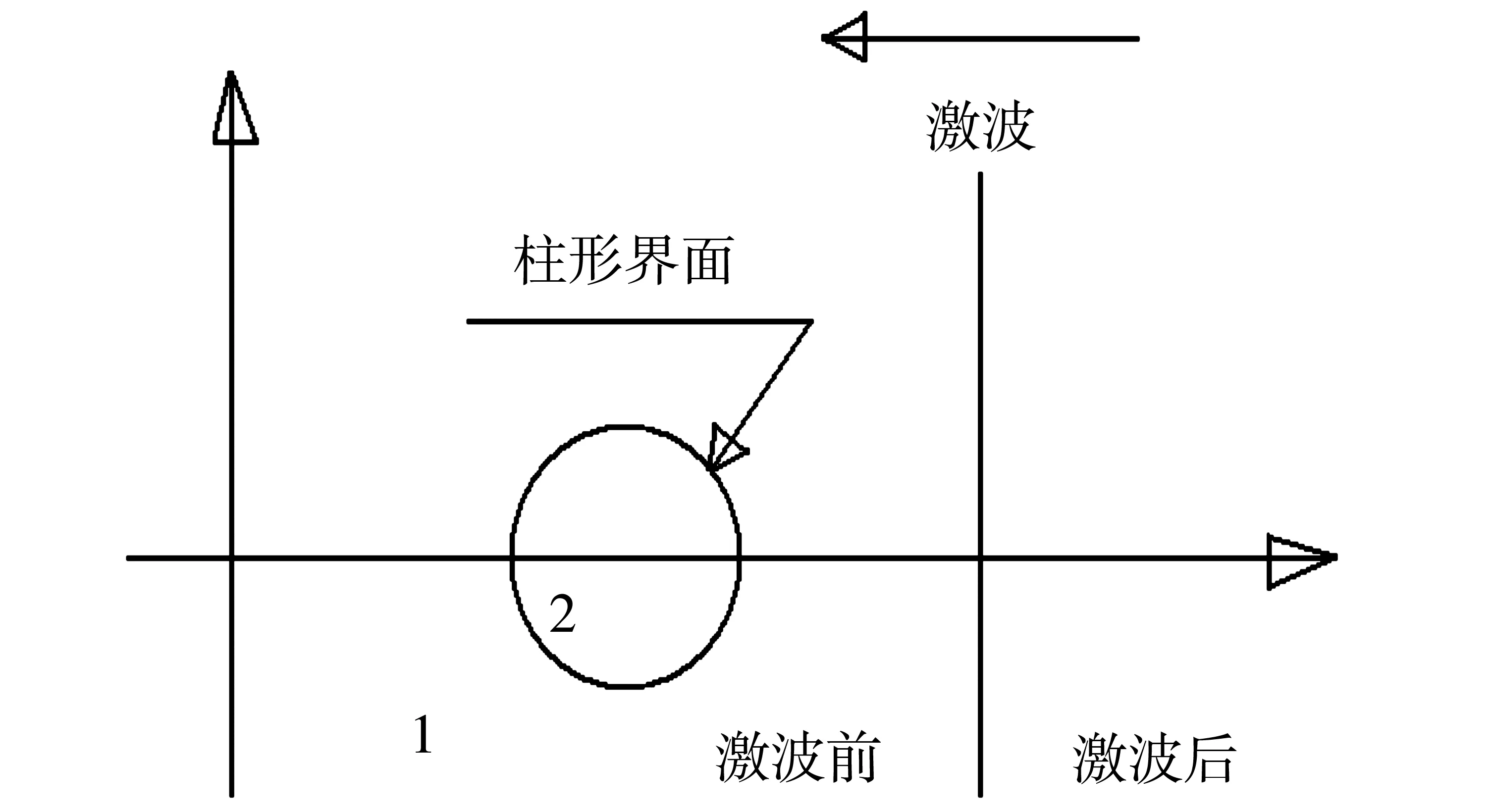
图4 初始时刻流场示意图

Level Set 方程的初值条件为

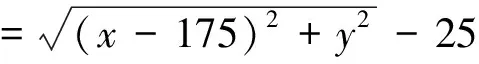
边界条件：左边界取出流边界条件，右边界取入流边界条件，即给定激波后的压力、密度和速度值，上、下边界取固壁边界条件。由图5给出t=18时刻的密度分布图并与实验结果相比较。图6给出t=38时刻的密度分布图并与实验结果进行比较。

图5 t=18时刻的等密度分布图

图6 t=38时刻的等密度分布图

图7、图8分别给出不同时刻的密度分布图。本文与Hass[12]等人的实验结果相比较发现，模拟出来的气泡变形与实验图形基本相符合，当激波与气泡相互作用时，产生了折射波和反射波，在激波扫后界面被压扁,并随时间的推移，气泡的右边基本保持原来的形状，而左边凹陷。本方法在激波与柱形界面相互作用的计算中取得良好的结果，数值结果与实验是吻合的。

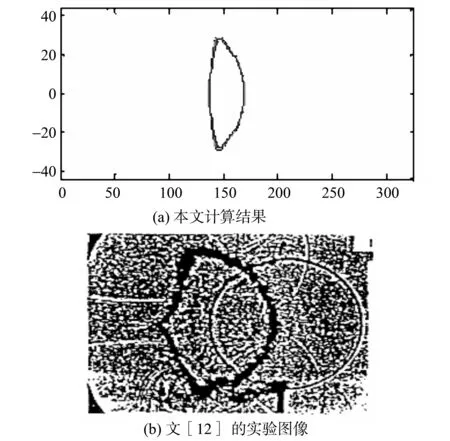
图7 t=108时刻的等密度分布图

图8 t=320时刻的等密度分布图

4 结 论

本文基于迎风紧致群速度控制方法求解流场控制方程，采用群速度方法克服激波附近非物理振荡，采用Level Set方法追踪运动界面。本方法在激波与柱形界面相互作用的计算中取得良好的结果，数值结果与实验是吻合的。

参考文献：

[1]YEE H C,WARMING R F,HARTEN A.Implicit total variation diminishing TVD schemes for steady-state calculations [J].Journal of Computational Physics,1985,57(3): 327-360.

[2]HARTEN A,ENGQUIST B,OSHER S,et al.Uniformly high order accurate essentially non-oscillatory schemes III [J].Journal of Computational Physics,1987,71(2):231-303.

[3]SHU C W.Numerical experiments on the accuracy of ENO and modified ENO schemes [J].Journal of Scientific Computing,1990,5(2): 127-149.

[4]LIU X D,OSHER S,CHAN T.Weighted essentially non-oscillatory schemes [J].Journal of Computational Physics,1994,115 (1): 200-212.

[5]LOMBARD C K,BARDINA J,VENKATAPATHY E,et al.Multi-dimensional formulation of CSCM—an upwind flux difference eigenvector split method for the compressible Navier-Stokes equations [C]// New York: American Institute of Aeronautics and Astronautics,1983: 649-664.

[6]张涵信.无波动无自由参数的耗散差分格式 [J].空气动力学报,1988,2: 143-165.

[7]马延文,傅德薰.计算空气动力学中一个新的激波捕捉—耗散比拟法 [J].中国科学：A辑(数学),1992,35(3): 263-271.

[8]FU D X,MA Y W.A high order accurate difference scheme for complex flow fields [J].Journal of Computational Physics,1997,134: 1-15.

[9]ZHU Q Y,LI Y.An upwind compact approach with group velocity control for compressible flow fields [J].International Journal for Numerical Methods in Fluids,2004,44: 463-482.

[10]FEDKIW R,ASLAM T,MERRIAN B,et al.A non-oscillatory Eulerian approach to interfaces in multimaterial flow (the ghost fluid method ) [J].Journal of Computational Physics,1999,152(2): 457-492.

[11]傅德薰.流体力学数值模拟 [M].北京: 国防工业出版社,1994.

[12]HASS J F,STURTEVANT B.Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities [J].Journal of Fluid Mechanics,1987,181: 41-76.