有趣的重写系统

陈凯

本文通过字符串的重写过程，模拟冯·诺依曼架构计算机的工作流程。需要的工具，可以从一支笔、一张纸开始。

● 纸笔计算机

该计算机的输入设备是笔，存储设备是纸，输出设备即纸上的墨水痕迹，运算器和控制器（CPU）暂由人脑替代，而运行的指令很简单。步骤一：只要看见0，就改成1001；步骤二：重复步骤一。可以将这些指令写在另一张纸（另一个存储器）上。接下来看看纸上的运算过程：①用户输入0，存储到纸上；②从另一个存储器调用指令：“只要看见0，就改成1001”；③运算：将0改成1001，将结果存储到纸上；④重复步骤一，运算结果是1001变成1100110011，存储到纸上；⑤重复步骤一，运算结果是1100110011变成1110011001111001100111……

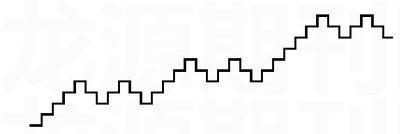
可惜这个过程不会自动终止，不过当存储器溢出（一张纸上写不下了）或者CPU崩溃（耐心耗尽）的时候，这个纸笔计算机自然就会停下来了。假设得到的结果是这么一长串数字：1111001100111100110011111100110011110011001111，这串数字有什么好玩的地方呢？接下来，看见1就往上画一格楼梯，看见0就往下画一格楼梯，从而完成纸笔计算机的输出过程。仔细观察后可看出有意思的地方，想象两个人分别从两端往中间走，两个人方向转折的步调是一致的，并且，如果将楼梯从中间一分为二，每一小部分楼梯图案仍然具有步调一致的模式，由此类推，这就是自相似（如下图）。纸笔计算机能运行到这个份上，也算功德圆满了，不过人的细心和耐心实在是比不上真正的计算机，下面，就来DIY一个真正的重写系统。

● DIY重写系统

1.“只要看见0，就改成1001”这个指令，可以用写字板的“全部替换”功能实现，这么一来，想要把字符串变换得多长都可以。

2.当得到一长串字符串后，用绘图指令将0和1替换掉。

3.在Logo环境中加载并运行代码，就能得到这张对称的楼梯图案了。不过更神奇的地方是可以随心所欲地用不同的绘图指令替代字符串中的0和1。例如，用“ fd 6 rt 45 ”替代“0”。用“ fd 6 lt 45 ”替代“1”，这样会得到怎么样的结果呢？

● 存储程序思想

在本文中，使用的重写规则是“只要看见0，就改成1001”，实际上，规则可以有各种各样的可能，并且可以由不止一行指令构成。可以将不同的规则看成是存储在计算机中的不同的程序，只要调用不同程序，上述改写系统便能绘制出完全不同的图案，而不需要对改写系统流程本身做什么调整。有兴趣的话，不妨试一下，以下规则重复调用两次后，生成的图案是怎样的呢？用户输入是01101。运算规则是，步骤一：只要看见0，就改成0aa00；步骤二：只要看见1，就改成01101；步骤三：只要看见a，就改成1；步骤四，重复执行前面步骤。图形输出方法是，只要看见0，就前进并左转90度；只要看见1，就前进并右转90度。（答案在本期找）