小学数学教学细节案例反思与对策

梁兆秀

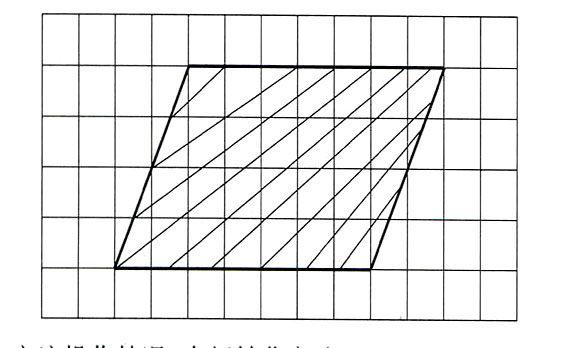
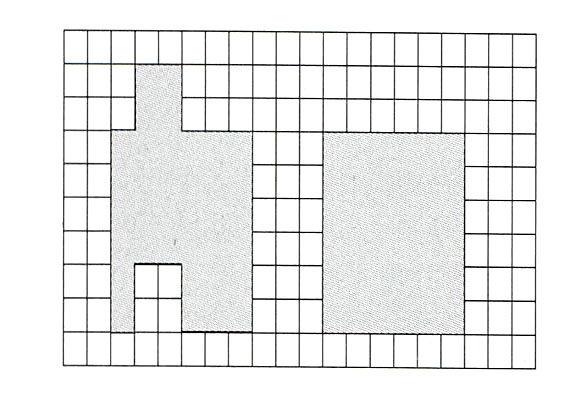
下面是“平行四边形面积计算”一节课的教学片段：

１． 出示两个图形. 提问：这两个图形面积相等吗？你是怎样想的？在小组里交流.

学生交流思考方法，教师指出可以应用转化的方法比较两个图形的大小. 揭示课题.

２． （１）出示画在方格纸上的平行四边形，学生操作，把平行四边形转化成长方形.

（2）交流操作情况，介绍转化方法.

（3）讨论：为什么沿着高剪开？

３． （１）提问：是不是任意一个平行四边形都能转化成长方形？平行四边形转化成长方形后，它的面积大小有没有变？与原来的平行四边形有什么联系？

（２）操作：从教科书的附页上选一个平行四边形剪下来，先把它转化成长方形求出面积，再填写下表.

（3）小组讨论：

① 转化成的长方形与平行四边形面积相等吗？

② 长方形的长和宽与平行四边形的底和高有什么关系？

③ 根据长方形的面积公式，怎样求平行四边形的面积？

（４）反馈、交流，抽象出面积公式.

分析——多想几个为什么

这是我们非常熟悉的教学过程，许多老师都是这样教的，在多次听课过程中，笔者也发现不同的课堂中与此相似的过程，我们已经见怪不怪了. 平行四边形面积计算的推导，就是把平行四边形转化成长方形，其方法是平移、割补，其间渗透的是转化的思想. 在课堂上，教师组织学生通过操作、交流、讨论，探索出平行四边形的面积公式. 但不知我们老师有没有思考过这样一个细节问题：完型表格的直接呈现，已经向学生暗示了平行四边形的面积与它的底和高“有关系”，平行四边形转化成长方形，平行四边形的底、高与长方形的长、宽“有关系”. 为什么探讨平行四边形的面积计算只考虑它与底和高的关系，而不是其他因素呢？为什么要把平行四边形转化成长方形呢？

对策——体会由来真理解

笔者认为首先让学生明白平行四边形的面积是由什么决定的，这是研究平行四边形面积计算方法的关键. 教学时，可先让学生猜想平行四边形是由什么决定的，教师再辅以演示来验证学生的猜想. 第一步，演示平行四边形的一组对边逐渐同步延长，夹角及另一组对边的长度不变，感知平行四边形的面积与边的长度有关；第二步，各边长度均不变，一组对角由小到大变化，让学生感受到平行四边形的面积与夹角大小有关，而边一定时，夹角的大小决定了平行四边形的高，从而得出平行四边形的面积是由底和高决定的. 学生体会到平行四边形的底和高决定它面积的大小，就会急于知道它们之间的关系，可先让学生猜想，再验证. 怎样验证呢？当学生想到把平行四边形转化成长方形计算面积时，教师可通过引导性提问让学生领悟长方形的面积计算我们已经学过，这里是“化新为旧”. 再通过操作探索平行四边形的面积，探索的思维指向性明确了，表格的揭示也就瓜熟蒂落了. 这样学生能真实体会“平行四边形面积等于底乘高”的由来，真正理解面积大小与底、高之间的联系.

反思——注重细节保有效

不管是现在的新课程改革，还是课改之前的教学，我们都倡导课堂教学的有效性. 怎样让我们的课堂更有效，怎样让我们的教学更高效？我觉得我们在教学过程中，不仅要让学生知其然，更要让学生知其所以然. 数学知识的形成是一个漫长的过程，蕴含着人们丰富的创造性发挥. 学生学习数学知识，就是将前人的经验转化成自己的知识财富的复杂过程. 新教材更多地给学生操作、讨论、交流、探索新知识的机会，但是由于一些因素的限制，教材中许多思维价值丰富的知识发生过程被简化，只能保留精炼、本质的逻辑结构. 教师在组织学生探索的过程中，千万不能简单照搬教材，使探索活动流于形式，浮于表面. “平行四边形面积计算”这一课，如果没有让学生明白平行四边形的底、高决定它面积的大小，那教师后面提供的体现探索过程与成果的表格，让学生通过平行四边形底、高、面积的填写，发现它们之间的关系，不就显得仓促与简单了吗？为什么计算面积只要考虑它与底、高的关系，不考虑其他因素呢？表格，其直接出示，导致学生的探索被代替，学生缺乏深刻的探索体验过程，只是跟在教师后面转的机器而已，这样的探索是一种虚假的探索. 只有当学生明白了底、高决定平行四边形面积的大小，急于探讨它们之间的关系，这时再出示表格就能进一步促进学生探索下去，这才是在学生自己具有一定思维指向性基础上的探索，“我要探索什么，我为什么要探索它？”而不是人为地提供探索的方向.

我们在引导学生开展探索活动时，不能简单地照搬教材，应以有效探索为目的，注重对教材的二度开发与合理加工，让学生通过自主探索，真正经历知识形成的过程. 学生的自主探索，既要有利于教学的合理进展，又要有利于学生对知识的真正获得，还要有利于学生思维的发展和创新精神的培养，这才是有深度、有效的探索.