类比学习法在初中数学课堂中的实践

徐贤成

【摘要】 数学知识和数学思想方法就是数学的核心. 提高学生分析问题、解决问题的能力是数学学习的重要目标之一. 本文研究对基于类比学习法的初中数学案例教学进行了分析和阐述，对初中数学课堂教学提出了对策和建议.

【关键词】 类比学习法；初中数学；案例

１． 引言

“数学是研究数量关系和空间形式的科学. 数学学习的本质就是以数学知识为载体促进学生思维的发展. ”

由此可见，数学知识和数学思想方法就是数学的核心. 学生的学习方法的获得往往要比知识的获得还要重要，数学方法不仅仅是我们学习数学的工具，也是学习其他学科的工具，甚至在生活中它能使复杂问题简单化，往往能起到事半功倍的效果. 这就提醒我们在教学中应特别注意数学方法的讲解与渗透.

我们怎样把“新课标”的理念和数学思想方法融入在日常教学中呢？新的《数学课程标准》告诉我们“数学的教学活动是师生共同参与、交往互动的过程. 有效的数学教学活动是教师教与学生学的统一，学生是数学学习的主体，教师是数学学习的组织者与引导者. ” 要提高学生分析问题、解决问题的能力，教给一些比较完整的解决问题过程和常用方法是十分必要的.

２． 基于类比学习法的初中数学课堂教学

数学方法有很多种，如类比、观察、实验、归纳、演绎、分析与综合、分类、反证法、数学归纳法等. 每一种方法都有各自的特点和作用，在初中阶段很多方法都渗透于数学教学活动中，这些都要灵活掌握和运用. 类比是重要的学习方法之一. 笔者结合平时教学过程中的一些收获，谈谈类比学习法在初中数学课堂中的实践.

类比是将一类事物的某些相同方面进行比较，以另一事物的正确或谬误证明这一事物的正确或谬误. 它是科学研究最普遍的方法之一，在数学中，类比是发展概念、定理、公式的重要手段，也是探索问题、解题的一种重要方法. 在数学课堂中，无论是新授课、还是复习课、特别是数学活动（课题学习）中，都渗透着类比思想方法.

案例一（新授课片段）

在八年级下学期１０．４ 探索三角形相似的条件第一课时的学习过程中，此时学生在七年级探索三角形全等的条件时积累了丰富的经验，同时在１０．３的学习中也学习了相似图形的概念、相似三角形的概念及判定方法（概念），因此，为我们利用纵向类比法进行学习做好了操作方法和课前知识的充分准备.

教学时，通过几组问题的问与答（见表１），来引入探索三角形相似条件的学习过程：

数学知识之间存在着紧密的联系，新知识往往是若干已有知识的重新组合或是已有知识的引申和扩展. 此处，我们与判定两个三角形全等的条件类比，使学生感悟判定两个三角形相似也可以适当减少条件，从而加强了数学知识间的纵向沟通，同时又鲜明地展示了数学知识的获取过程，形成清晰的知识网络，把新知识纳入原有的认知结构中，使学生将所学知识条理化、系统化，我们形象的说：“点串成了线”.

案例二 （复习课片段）

“类比的出发点，是对象之间的相似性，而相似对象又具有多种多样的属性，在这些属性之间又有这样和那样的关系，人们对这些关系的认识过程，是从简单到复杂的过程. ”

在学习反比例函数课程之后，学生之前已经学习了一次函数（正比例函数），所以对函数概念及其意义有了较为深刻的了解. 复习课上，先通过正比例函数与反比例函数表达式、图像等直观的对比（见图１），由易到难，由简到繁，从而加强了数学知识间的横向沟通.

在掌握基础知识和基本技能的基础上，运用类比的方法，再次把一次函数引入复习，师生共同设计表格（见表２）.

对三种函数从式到形、由单一到复杂，展开丰富的联想，产生迁移，形成新的观点，使原有知识结构得到补充、改造和逐步完善，夯实“双基”，开阔学生的知识领域，提高思维的创造性，实现认知上的飞跃. 运用类比的方法，横向拓宽知识，我们形象的说：“点连成了线”.

案例三 （活动课）

数学活动课是一种以学生活动为主要形式的课程. 它注重学生的实践，着眼于丰富知识、发展智力，培养学生主动探索和综合运用知识的能力，而且集思想性、知识性、趣味性于一体. 下面我们就以“数学活动：设计包装纸盒”来谈谈如何把数学知识和方法渗透进教学中来.

【问题情境】

提出问题：３０块肥皂：８ ｃｍ × ５ ｃｍ × ３ ｃｍ，厂家想把３０块肥皂装箱，如何设计纸箱使得用料尽可能少？

【建构活动】

① 一块肥皂：８ ｃｍ × ５ ｃｍ × ３ ｃｍ.

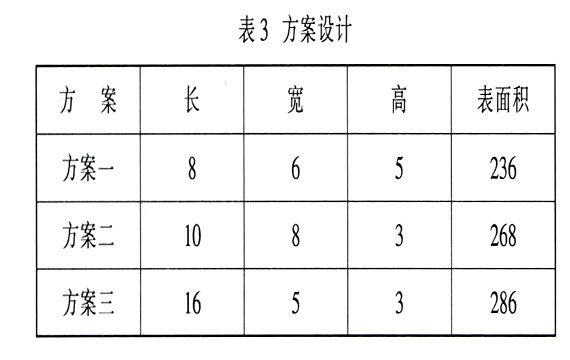
② 两块肥皂：学生小组讨论，合作交流：（见表３）

③ 四块肥皂：生产这种肥皂的厂家为了扩大销售量， 准备“买３送１”，捆绑式销售. 如何设计“装４块肥皂”的包装盒呢？

（1）要求：设计包装纸盒，恰好装进４块肥皂，不留空隙；

（2）小组合作，填好记录表，画出包装盒的平面图；

（3）推选代表，演示设计方案，展示平面图，分享经验和方法；（见表４）

归纳小结：体积一定的长方体纸盒，如何设计长、宽、高，使得盒子用料最省. 体积一定的长方体，长宽高越接近，用料越少．

【解决问题】 ３０块肥皂：８ ｃｍ × ５ ｃｍ × ３ ｃｍ.

该肥皂厂家想３０块肥皂装箱，如何设计纸箱使得用料尽可能少？

３． 教学结论与改进

解决一个复杂问题时，可以先解决一个特殊情况，然后对解决特殊情况时所用的方法、所得的结论进行分析，把它与一般情况进行类比，分析在一般情况下能否作类似处理. 这样，“从数到形、再从形到数”，“由特殊到一般”综合本学科前后知识、学科之间的关联知识，可以帮助学生贯通知识间的联系，使知识融会贯通，形成系统有效的知识网络，逐步构建良好的认知结构，从整体上掌握知识. 笔者认为，这种数学活动（课题学习）的不断开展，最终会使学生的认识由表面特征的感性认识阶段上升到对内部本质属性及规律的理性认识阶段. 我们形象地说：“线织成了网.”

由于问题往往是错综复杂的，解决问题的手段和方法也是多种多样的，所以教师要把过程与方法讲得粗细适当、不把方法挂在口边、过分强调. 波利亚指出：“问题解决的基本过程是：对问题有一个比较准确、清楚的认识；拟定解决问题的计划；实施计划（在实施计划过程中要对计划作适时的调整和补充）；回顾与总结. ”一定要把握住学习活动重在学生的主体活动，重在方法的渗透.

知识是基础，方法是中介，思想是本源. 数学是能够增长学生智慧的学科，特别是初中课堂，我们要抓住数学本质，与新课程理念有效结合，这样才能发挥数学教育的最大价值，实现人人在数学上的发展，收获行之有效的方法，为日后的发展奠定知识和思想方法的基础！

【参考文献】

［１］张翠萍． 课堂教学如何有效地指导学生自主探索［Ｊ］． 新课程（小学版）， ２００６，（１１）.

［２］方钟成． 构建富有活力的数学课堂［Ｊ］． 福建论坛（社科教育版）， ２００７，（０１）.

［３］包朝龙． 问题目与问问题［Ｊ］． 教学月刊（中学版）， ２０１０，（１０）.

［４］符祖河． 浅议课堂教学中自主探究能力的培养［Ｊ］． 管理观察， ２００９，（１５）.