在参与中体验 在活动中发展
【教学设计思路】
义务教育课程标准人教版小学数学实验教科书中有关三角形的知识分几个阶段教学,本课是四年级上册第82页的教学内容,教学的重难点是应用数据发现三角形三边的关系,理解“任意”的含义。
杜威曾说:“一盎司经验胜过一吨理论。”任何的理论研究都抵不上亲自实践和体验来得真实和深刻,新修订的《数学课程标准》在“双基”的基础上提出了“四基”,即基础知识、基本技能、基本思想和基本活动经验。这就要求我们的数学教学在继续保证“双基”的基础上,还必须让学生充分经历学习过程,积累数学活动的基本经验。因此,在教学《三角形三边之间的关系》这节课时,我精心设计了一系列的数学活动,让学生在参与中体验,在活动中发展。课堂上,学生通过自动操作、自动估猜、自动探索、自动迁移,深入认识三角形。通过师生之间、生生之间充分的交流合作,使学生体验到数学学习的乐趣,让学生自然、自动、自由地发展。
【教学过程】
一、生活激趣,引入新课
图1
师:同学们,看,一个绿草茵茵的公园里有块漂亮的花圃。一只调皮可爱的机灵狗在A点玩耍,如果它要跑到C点,有几种不同的走法(如图1)?
生:两种。(课件闪动两条路)
师:小狗在玩耍中,忽然闻到从C点飘来的阵阵骨头香味(课件出示香喷喷的骨头)它会按怎样的路线马上扑向骨头?请一个学生上台指一指。(A-C)(课件显示路线)
师:不错!机灵狗这么走马上吃到了香喷喷的骨头!(课件显示狗吃到骨头)为什么走这条路线?
生:这条路线最近,走的路最短。
师:大家说得都很有道理,直接走比走这两条路的总长度(课件演示路线)近一些。其实,这个花圃可以看做一个什么形状的图形?(课件抽象成三角形)
师:三角形是很奇特的图形,有很多有趣的数学问题等着大家去研究。今天这节课,就让我们再次走进三角形的世界,去探究其中的奥秘。
【设计意图:生动有趣的情境呈现,使学生眼前一亮。为了让小狗较快地吃到香喷喷的骨头,学生不由自主地、非常自然地展开思维活动:走哪一条路近一些?直觉告诉孩子:走AC这条路比走AB与BC两条路的总长度近一些,从而为研究三角形的三条边之间的关系埋下伏笔。“为什么小狗直接走的一条路就是近的,而走另外两条路的总长度就是远的?”这引出了继续深入地研究三角形的需要。】
二、合作探究,体验感悟
1.动手操作,自主探究
师:你们知道摆一个三角形需要几根小棒?
师:那么,给你3根小棒,是不是一定就能围成一个三角形呢?老师这里有三根小棒,谁来试一试?
师:围成了吗?怎么就没围成呢?是操作不当还是另有原因,需要老师帮忙吗?还是不行,看来并不是操作不当,想一想,到底是什么原因呢?
师:如果只让你改动一根小棒的长度,你想怎么改,就能围成一个三角形呢?
师:看来三根小棒能不能围成一个三角形,是和小棒的什么有关系?
生:和小棒的长短有关!
师:你们的想法都不错!我们如果让黄色或红色小棒变长,是不是越长越好?如果缩短绿色小棒的长度,是不是越短越好?带着这样的思考来进一步研究三角形。
2.数形结合,初步感知
师:请看,这两根小棒的长度不变,我们从缩短绿色小棒的长度来思考,猜一猜,绿色要缩短到多少厘米就能围成三角形呢?我们只说整厘米数,谁来猜猜?
师:大家都能大胆地猜想,其实生活中许多重大的发现都是从猜想开始的,可是仅猜还不行,我们更要在实践中加以一一验证。接下来我们就通过折一折的方法来验证自己的猜想。
师:看!每组桌上都有一些标有刻度的小棒,红色都是6厘米长,黄色都是3厘米长,绿色的长度不同。我们先把小棒按颜色沿着刻度折一折,分成红、黄、绿三段,然后再看一看这三段能不能围成一个三角形。
生:围成了。
师:因为红、黄、绿的长度是固定的,所以不管折出的3段能否围成三角形,都要数出3段的长度,写在白板上。
【设计意图:“经验”是看不见、摸不着的,而且还难以用直观的语言加以表述,因此必须利用操作来丰富学生的活动,让经验能够“摸得到、看得明”。这里教具的设计别具匠心,学生用可折的、带有不同颜色且标有刻度的磁条,按不同颜色折成三段,再把磁条放在白板上,观察是否能围成一个三角形,进而研究三角形三条边长度的关系。教具很适合学生操作、探究,大大提高了课堂教学中学生活动的效率,让每一个孩子都积累了丰富的数学活动经验。】
3.合作交流,揭示性质
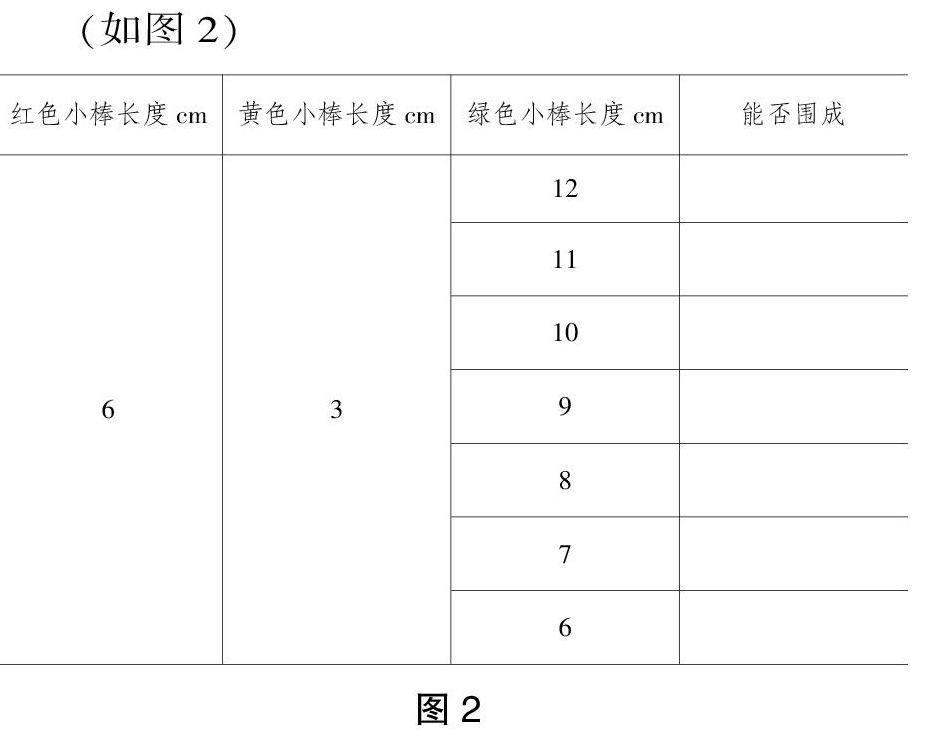
师:许多同学已经有了操作结果,大家来汇报一下,哪些能围成,哪些不能?
(如图2)
图2
师:长度是9厘米时,图形有些特殊,我们重点研究它。
生:不能围成。(学生操作,再次感知不能围成一个三角形)
师:大家仔细观察这张表格,什么变了?什么没有变?
生:绿色小棒的长度变了,红色和黄色的长度没有变。
师:回答得真棒,学数学就要会用数据去考虑问题!看,红色小棒的长度没有变,黄色小棒的长度没有变,由此,你能联想到它们长度的什么也没有变?
生:两根小棒长度的和没有变!
师:从大家的发言中,我听到了智慧的声音,以前我们总是考虑一根和另一根去比长,而现在却考虑到了用两根的和去与第三根进行比较,真了不起!
师:用两根小棒长度的和与第三根比时,(课件动态演示)你发现什么时候就可以围成三角形呢?互相讨论讨论!
生:红色和黄色的和比绿色大时,就可以围成一个三角形。
师:想一想什么时候就围不成三角形呢?
生:红色和黄色的和比绿色小时,就围不成一个三角形。(课件动态演示)
师:红色和黄色的和与绿色小棒的长度都是9厘米时,为什么不行?
生:因为6厘米和3厘米合起来刚好等于9厘米,所以围不成。
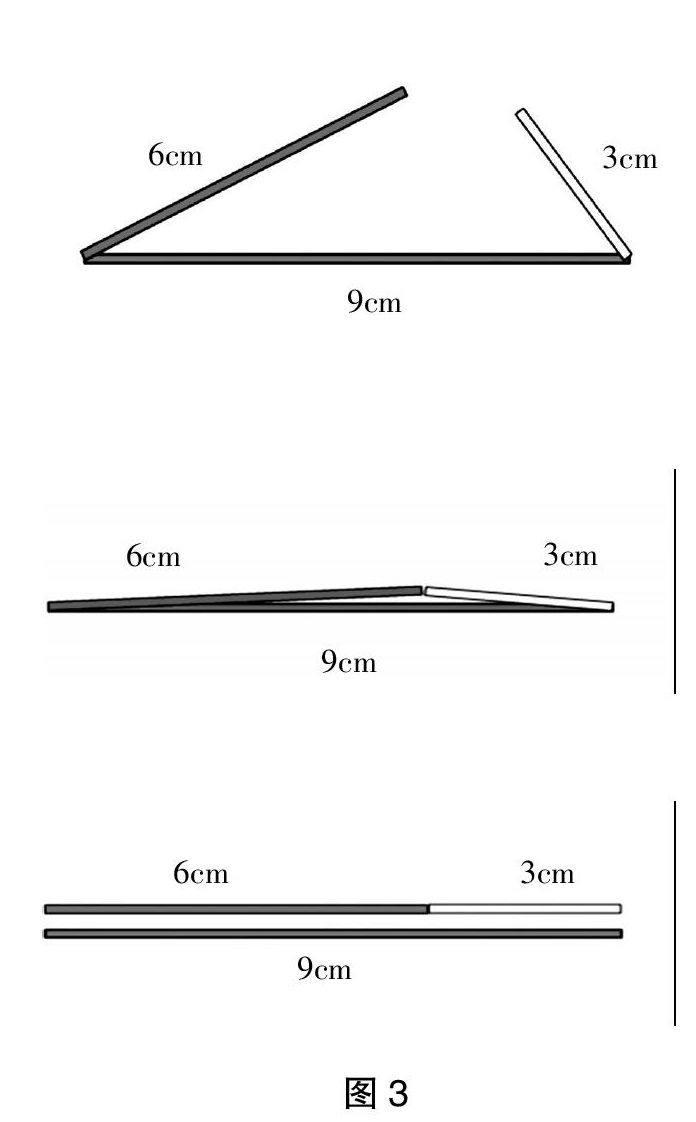
师:(课件动态演示)当红色和黄色的和与绿色相等时,是围不成三角形的。(如图3)
图3
师:通过刚才的探究,我们近一步清楚了两边之和与第三边的关系,这是判断三根小棒能否围成三角形的关键所在!
师:当两根之和大于第三根时——
生:能围成三角形。
师:当两根之和小于第三边、或等于第三边时——
生:不能围成三角形。
师:不错!我们以这个三角形为例,(红色长6厘米,黄色长3厘米,绿色长7厘米)我们已经知道红边和黄边的和大于绿边,也就是6+3>7,红边和绿边的和是不是大于黄边?用这样的式子怎么表示?6+7>3,谁再来说一个式子表示的绿边和黄边的和与红边的关系?(出示3组算式)
师:在这个图形中:12+6>3,12+3>6,三根小棒为什么不能围成一个三角形?(围不成的例子:红色长6厘米,黄色长3厘米,绿色长12厘米)
生:3+6的和比12少,或3+6<12。
师:对了,3+6<12,表示这组中两根之和小于第三根。也就是说三根小棒要围成一个三角形,任意两根的长度的和都要大于第三根才行。
师:通过猜想并再次验证,你发现三角形的三边长度之间有着怎样的关系?
生:三角形任意两边的和大于第三边。
师:现在我们回到课前:那只调皮的小狗完全凭嗅觉走这条路线直扑骨头,同学们能用今天所学的有关三角形的知识,来解释生活中的这一现象吗?
生:三角形两边之和大于第三边,这一条边小于两边长度的和,所以走这条路最近。
【设计意图:学生数学活动经验需要总结提炼。因此,教师要当好“引导者”。“三根小棒能否围成一个三角形?”表面上是在讨论围成或是围不成,但这之后隐藏着——三角形三边之间的关系。在老师的引导下,学生们发现,红色小棒的长度没有变,黄色小棒的长度没有变,由此想到它们长度的和也没有变。通过观察汇总的表格又发现,当两根小棒长度的和比第三根大时能围成三角形,当两根小棒长度的和小于或等于第三根时不能围成三角形……这是学生在数学活动中积累起来的丰硕成果。】
三、解决问题,应用新知
师:看着你们自己发现的这条规律,相信大家的心中一定充满了成就感。请看:
1.这组线段(6cm、2cm、5cm)能围成三角形吗?
师:为什么?你能说说理由吗?
师:可是我们刚才说的是任意两边的和大于第三边,只比了一组。其他的两组要不要比一比?
师:三条边中,长边本身就是最长,加上一条边肯定大于第三边。看来,在以后判断三条线段能否围成一个三角形,咱们只要计算两条短边的和是不是大于长边,这样判断快捷、方便!
2.5cm、5cm、5cm能围成三角形吗?
师:你能想出这个三角形的样子吗?
3.2cm、4cm、6cm能围成三角形吗?
师:2.1cm、4cm、6cm能围成三角形吗?
生:能,因为2.1+4>6。
4.2cm、3cm、8cm能围成三角形吗?
师:3厘米和8厘米不变,2厘米换上几厘米就可以呢?
(课件演示把2换成?)
生:大于5厘米就可以。
师:同意吗?好,大家都同意,那我们一起数整数,6、7、8——
师:同学们注意,线段的长度在不断地发生变化,三角形的形状在不在变化?
师:长11厘米行吗?先想一想图形的样子,再判断。
(课件演示长11厘米、12厘米的情况)
师:刚才,我们发现线段的长度和三角形的形状同时在改变。大家不能只看几加3大于8,还要从另一个角度,看8加3也要大于几,这样把数据和图形结合起来考虑问题会更全面,会让人越来越智慧!
【设计意图:人的水平、能力千差万别,学生亦不例外。如何利用学生已有的知识基础和经验基础引发学生反思,进行经验的迁移,促进智慧生成呢?这里开放分层的练习设计,使学生的思维像美丽的风筝在广阔的天空中自由飞翔,培养了思维的灵活性,广阔性。同时,“换成11厘米就不行了”是学生思维深刻性的体现,使学生对三角形三边之间的关系有了更全面、更深刻的理解。】
四、课内总结,课外延伸
师:同学们,这节课我们边做边想,先猜后验证,进一步认识了三角形。数学的研究是无止境的,大家在以后的学习中会发现三角形更多的奥秘!
【设计意图:这是一节具有生成性的课。从让学生动手操作,自主探究到到揭示三角形三边长度之间的关系,学生积累了丰富的数学活动经验,一切是那么的自然,是那样的水到渠成。课中,老师通过创设情境,形成问题,促使学生自然想学;分层指导,灵活训练,调动学生自动善学。正是由于老师把探索的时间与空间留给了学生,让学生自主探索、自由发挥,学生的聪明才智得以充分地施展,这样的课堂也正是大家所梦寐以求的。】
(朱艳峰,南通市国棉一厂二三工小,226000)

