位置伺服系统的自适应积分滑模控制研究

高远，孔峰，罗文广，谭光兴

（广西工学院 电子信息与控制工程系，广西 柳州 545006）

1 引言

伺服系统广泛应用于机器人装置、数控机床等自动化设备。伺服系统往往受到机械参数时变、外部扰动或工作条件的不确定性影响。现代伺服系统通常与计算机相结合，因此对于高性能的伺服系统，一般要求其具有精度高、无超调、响应速度快且鲁棒性好等特点。近年来，人们为提高伺服系统的控制品质，提出了一些有效的控制方法和技术［1－2］。

滑模变结构控制是一种非线性鲁棒控制器，具有算法简单、易于实现、鲁棒性强等优点，在伺服系统控制领域中具有良好的应用前景。然而，由于滑模控制系统存在切换开关非理想等因素的影响，会产生控制作用的抖振效应。抖振效应会增加机械磨损和能量消耗，甚至可能激发高频未建模动态等［3］。为提高滑模控制的性能品质和降低控制抖振效应，人们采用具有平滑特性的饱和函数或双曲函数来代替具有开关特性的符号函数［4－5］，但单纯的符号函数修正缺乏控制的自适应性。基于自适应律的滑模切换面、控制趋近律或与智能算法相结合的滑模控制方法在很多场合优于传统控制的效果，且具有较好的控制自适应性［6－8］。

本文为提高滑动模态中位置伺服系统的控制性能，研究采用比例积分微分滑模切换面，推导出滑模控制器的等效控制器表达式，并提出一种具有自适应律特性的切换控制器形式。理论上对滑模控制器的稳定性及抖振效应进行了分析。采用英国Feedback公司生产的模块化直流伺服系统MS－150开展实验研究。实验结果表明：本文所提出的自适应积分滑模控制器（adaptive integral sliding mode controller，ASMC＋I）相比传统的滑模控制器（sliding mode controller，SMC）以及比例－积分－微分（PID）控制器而言，具有更好的控制性能，且较好地降低滑模控制所固有的抖振效应。

2 直流伺服系统的数学模型

直流伺服系统的结构示意图如图1所示。通常其数学模型可表示为

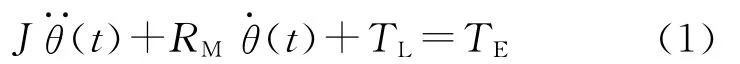
式中：J为折算到电动机轴上的转动惯量；RM为电机阻尼系数；θ（t）为电动机的转角位置；TL为外部负载扰动和非线性摩擦；TE为电机电磁转矩。

当输入恰当的控制电流i（t），电磁转矩具有关系

式中：Kt为电动机转矩系数。

将式（2）代入式（1）中并整理有

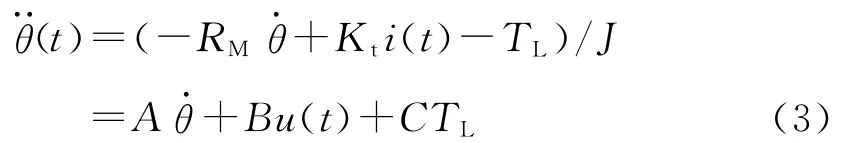
其中A＝－RM／JB＝Kt／J＞0C＝－1／J采用控制作用符号u（t）来表示电流i（t）。

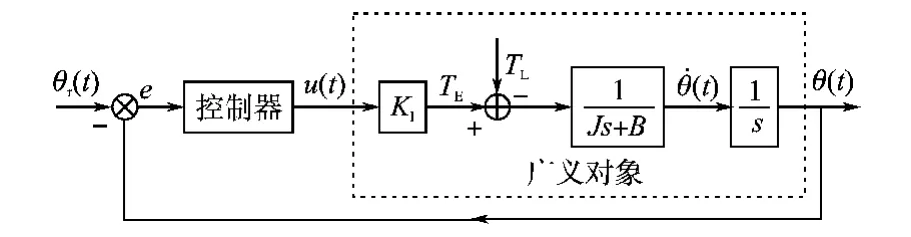
图1 直流伺服系统的结构示意图Fig.1 Block diagram of DC servo system

考虑实际伺服系统存在着电机参数、外部负载的时变性，非线性摩擦以及模型中不可预测的不确定项，那么电机伺服系统的实际模型可表示为

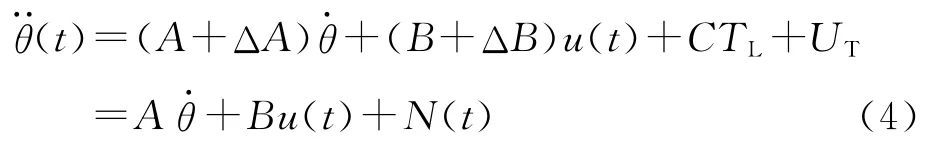
式中：ΔA和ΔB为由系统系数J，RM和Kt引起的参数变化；UT为由非理想电流、暂态过程中磁场定向控制或实际控制中非建模动态特性引起的非建模不确定性；N（t）为上述所有不确定性的总和。

即N（t）为

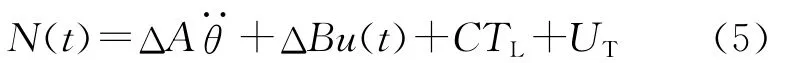
假设｜N（t）｜≤Nm＞0，Nm是不确定性因素总和的上界。

当转角位置θ（t）跟踪某给定的期望位置信号θr（t），引入跟踪误差e（t）

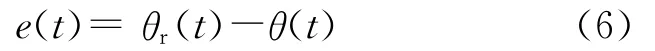
则可根据式（4）得到误差方程

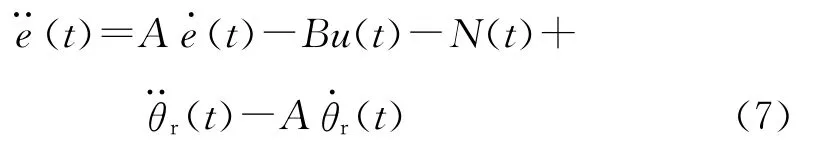
当设计恰当的控制器u（t），使得当t→∞时，e（t）→0，那么伺服系统的控制目标将得以实现。

3 自适应积分滑模控制器设计

3.1 积分滑模函数

传统SMC的滑模函数S（t）依赖于跟踪误差e（t）及其变化，它常表示为［9］

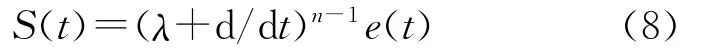
式中：n为被控系统的阶数；λ为常数λ∈R＋。

对于二阶系统（n＝2），通过控制所获得S（t）＝0的解是与式（8）相联系的二维相平面里通过原点的一条确定性直线。然而，当存在干扰作用，误差e（t）将不再与滑模面相吻合。由于在伺服系统和其他工业应用的控制问题中，零稳态误差往往很重要。为了提高在干扰情况下零稳态误差的控制性能，本文对式（8）引入积分环节，即［10］

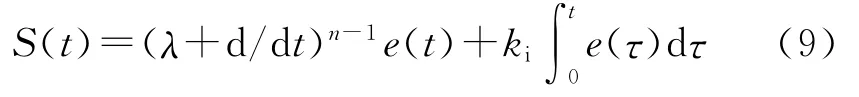
式中：ki是积分增益，且ki∈R＋。

引入积分环节后，当n＝2，通过控制所得到S（t）＝0的解将是与式（9）相联系的三维空间中通过原点的平面。

3.2 控制器设计

滑模控制器u（t）通常主要包括针对确定性系统在无干扰情况下的等效控制ueq（t）和用于抑制不确定性干扰因素作用的切换控制us（t）两部分。即

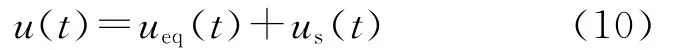
针对上述伺服系统的控制问题，在忽略不确定性因素情况下N（t）＝0，且当积分滑模函数满足关系：

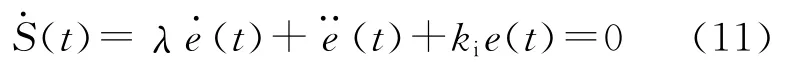
结合式（7）可以得到等效控制器

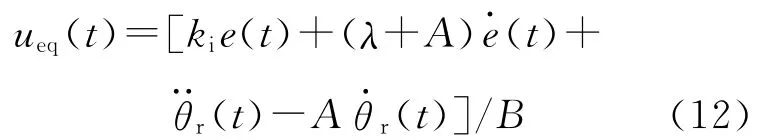
在无干扰情况下，ueq（t）的作用可保证系统跟踪误差e（t）从初始状态趋向积分滑模面S（t）＝0。当系统存在不确定性因素影响时，等效控制无法保证系统的控制稳定性，因此需要切换控制us（t）来抑制干扰的作用。

传统的切换控制器形式大都为

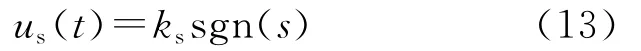
式中：ks为切换增益，ks∈R＋；sgn（·）是符号函数。

虽然传统的滑模切换控制器能保证伺服系统的滑动模态，并抑制外部干扰，但符号函数的非连续性所带来控制的抖振效应会造成系统机械损坏，甚至会导致控制系统失稳。人们虽然采用具有平滑特性的饱和函数或双曲函数来代替开关特性的符号函数，然而单纯的符号函数修正缺乏控制的自适应性，且消除抖振效应的效果有限。本文在文献［5］基础上，采用双曲函数tanh（·）代替传统的符号函数sgn（·），提出一种具有自适应特性的切换控制器

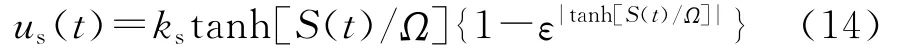
式中：切换控制增益ks为大于零的常数；Ω∈R＋是正常数，它可视为影响控制稳态精度和鲁棒性的切换带区域宽度［5］；ε为大于1的实数。

式（14）具有自适应规律，能反映控制作用随着｜S（t）｜大小进行调节的关系。｜S（t）｜越大，表明偏离滑模面距离越远，则需增大控制作用us（t）；相反，｜S（t）｜越小，表明趋向滑模面距离越近，则需减小控制作用us（t）；当｜S（t）｜＝0，则应有us（t）＝0。因此基于这种自适应关系，当实现控制目标时，切换控制的抖振效应降低到最小。根据式（10），滑模控制器可表示为

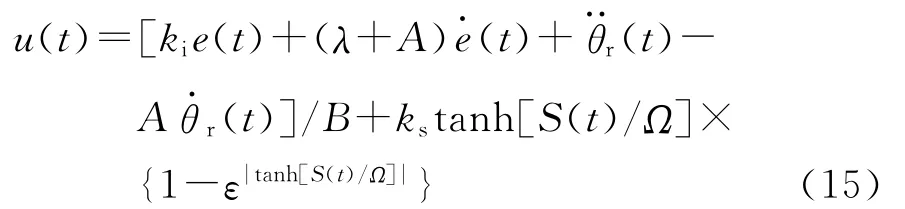
3.3 控制器稳定性分析

定义系统的Lyapunov函数

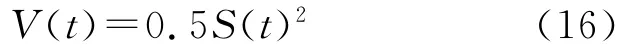
当S（t）≠0，V（t）＞0；仅当S（t）＝0时，V（t）＝0。在控制作用下，结合式（7）、式（10）和式（15）有

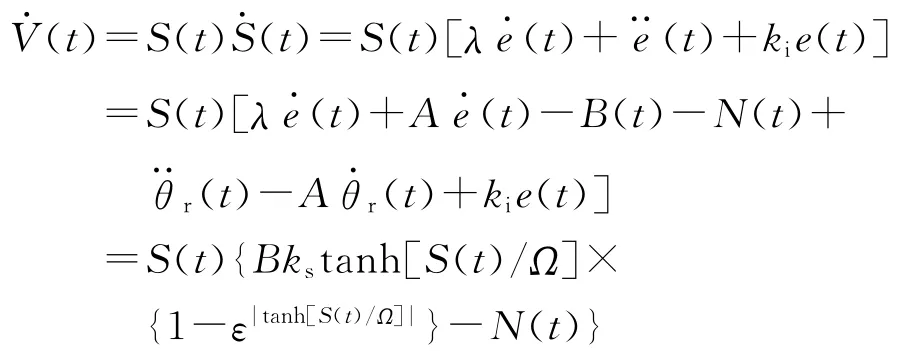
由于｜tanh［S（t）／Ω］｜≤1，可将ε｜tanh［S（t）／Ω］｜按泰勒级数展开

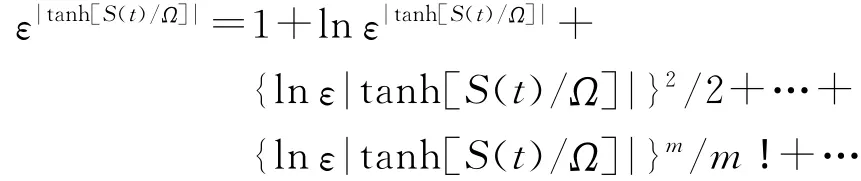
取展开式前2项，并利用xtanh（x）≤xsgn（x）＝｜x｜，且当ks＞Nm／（Blnε）＞0时，则有

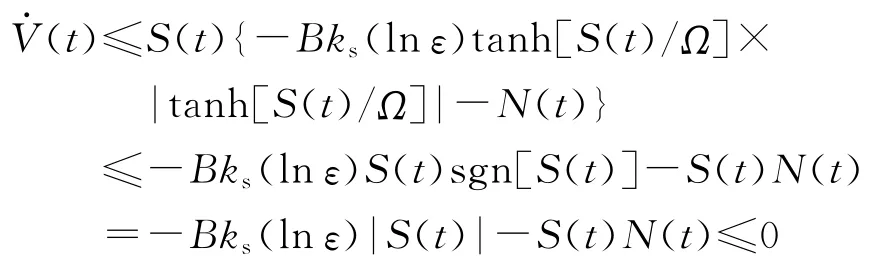
所以采用式（15）形式的滑模控制器，满足Lyapunov控制稳定性定理，即也满足滑模面S（t）＝0的到达条件［3－4］。

4 实验研究

为验证控制方法的有效性及可实现性，本文借助模块化直流伺服系统装置MS－150开展实验研究。

4.1 模块化直流伺服系统MS－150的简要介绍

英国Feedback公司生产的模块化直流伺服平台MS－150是一种适于控制理论教学和技术开发的实验设备。它与个人计算机（PC机）相结合所构成的实验设置框图如图2所示。图2中的被控对象位于虚线框内，它由Feedback公司提供的电压衰减装置、前置运放、伺服放大器、永磁直流电动机、减速装置、转角位置转换器（输出电位计）和电磁制动器等模块化器件构成。被控对象的实际转角θ经过轴转位置传感器OP150K后以电压信号形式输出，被控系统的控制输入电压u（t）通过计算机控制器得到。

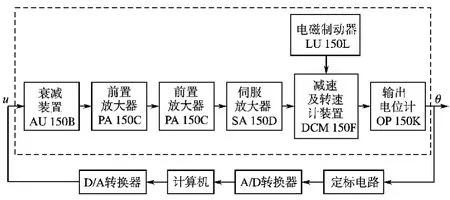
图2 实验设置框图Fig.2 Block diagram of experiment setup

在实验平台中，伺服放大器SA150D是1个双端输入和输出的功率放大器，它须与1个单端输入、双端输出的前置放大器PA15C相连接。前置放大器PA15C的输入电压范围在－0.25～0.25

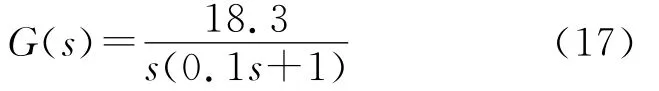
由式（17）可知相应的系统参数A＝－10，B＝183。

4.2 实验方案设计

基于 MS－150实验平台，采用 Matlab／Simulink工具箱设计出的实时控制模型图见图3。由图3可知，采集到的转角信号通过PCI1711接口卡进入PC机控制模块，并通过角度转换器把角度编码变换为模拟转角θ（t），θ（t）与期望θr（t）相比较得到转角误差e（t），e（t）通过微分器得到转速误差信号。为防止的高频成份易造成响应过程提前，导致系统的动态特性降低，实验中以通过一个二阶低通滤波器的信号来代替理论的转速误差信号。对应控制方法的控制器模块产生的控制激励u（t），它通过PCI1711接口卡作用于PC机外部的直流伺服电机系统。V，若输入电压超出该范围，则前置放大器和伺服放大器将工作在饱和状态。为提高容许电压范围，因此在前置放大器前端引入增益因子为0.1的衰减器AU150B，则被控系统输入控制信号的最大电压为2.5V。PC机承担提供期望转角位置、数据获取、实时控制和系统监控等任务，它通过接口卡PCI1711与外部硬件进行连接通信。A／D转换器、D／A转换器以及测量标定电路集成在转换电路装置33－301，通过该装置可完成相应信号类型的转换。

对于MS－150与PC机相结合的计算机伺服控制系统，它的实时控制程序既可基于Matlab／Simulink环境建立，也可以基于C／C＋＋语言编程实现。本文利用Matlab／Simulink环境实现上述控制方法。在空载情况下，MS－150中被控伺服电机的数学模型G（s）可通过辨识得到［11］

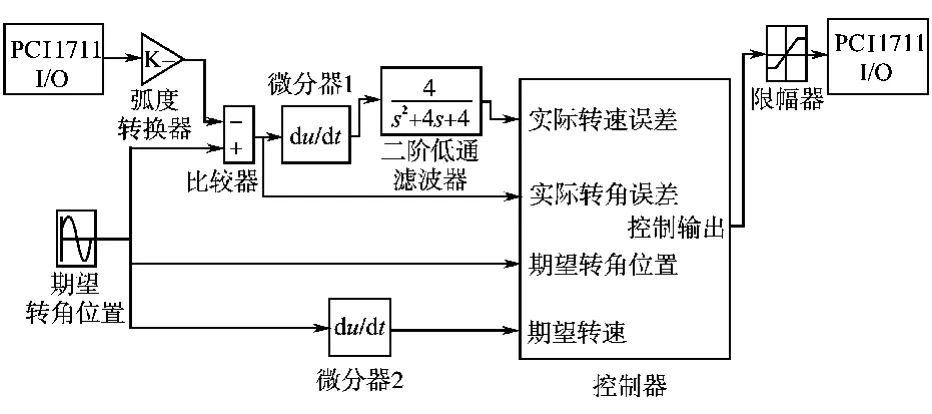
图3 基于MS－150的实时控制模型图Fig.3 Real－time control model based on MS－150

4.3 实验结果及分析

为验证本文所提出ASMC＋I控制方法的优越性，实验中将其分别与PID控制、传统的SMC控制进行比较研究。对于式（17）的被控模型，其PID控制器形式为［11］

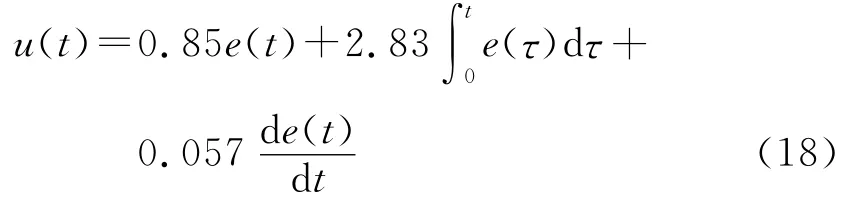
采用式（9）和式（13），并选择阈值为±1的饱和函数代替式（13）的符号函数设计出传统的滑模控制器（SMC），该控制器取滑模函数的参数λ＝20，ki＝0，切换控制器的增益参数为ks＝250。对于式（15）的ASMC＋I控制，积分滑模函数中λ＝20，ki＝0.6；切换控制器的增益参数为ks＝250，滑模带厚度Ω＝30，ε＝100。实验选择采样频率1kHz，并分别采用单位阶跃信号和频率为0.5 rad／s，幅度为1的正弦信号作为转角期望位置。当实验采用单位阶跃信号作为期望位置时，单位阶跃信号的导数被认为是零。

分别采用PID，SMC和ASMC＋I控制方法，伺服系统对阶跃信号的响应曲线图见图4。由图4可见：对于PID控制的阶跃响应，其超调量较大，稳态收敛时间较长，控制精度稍逊；对于SMC控制，控制虽无超调，但上升时间几乎与PID控制相同；对于ASMC＋I控制，控制性能最好。

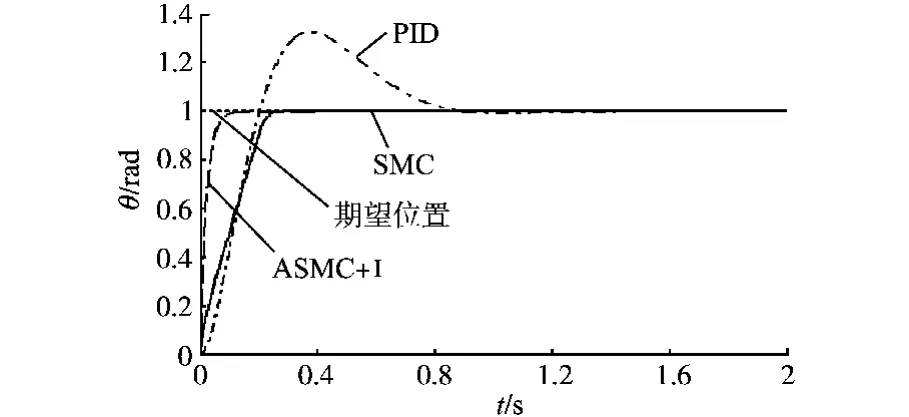
图4 不同控制方法的阶跃响应曲线图Fig.4 Step response curves for different control methods

选择期望位置为正弦信号θr（t）＝sin（0.5t），让PID控制器，SMC，ASMC＋I分别应用于实验设备。为验证各控制器的控制鲁棒性，伺服系统的控制输入加入幅度为1mV、均值为零、均匀分布的噪声以作为外界干扰对控制的影响。各控制实验结果分别如图5、图6和图7所示。由图5～图7比较看出，PID控制虽然能保证稳态误差在允许的范围内（e（t）≤5%），但控制精度逊于滑模控制，且控制器输出电压幅度较大；传统的SMC控制的控制精度有所提高，但输出控制电压抖振效应明显；ASMC＋I控制不仅可得到较为理想的跟踪性能，且能较好地削弱控制的抖振现象，使输出电压相对光滑。

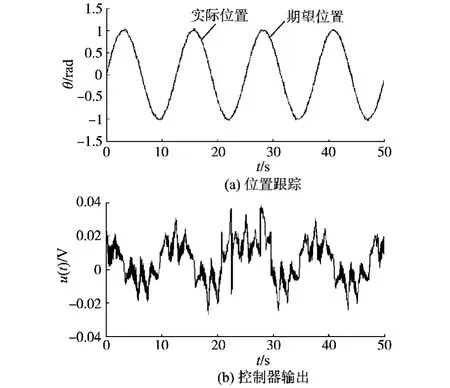
图5 PID控制的实验结果Fig.5 Experimental results of PID control

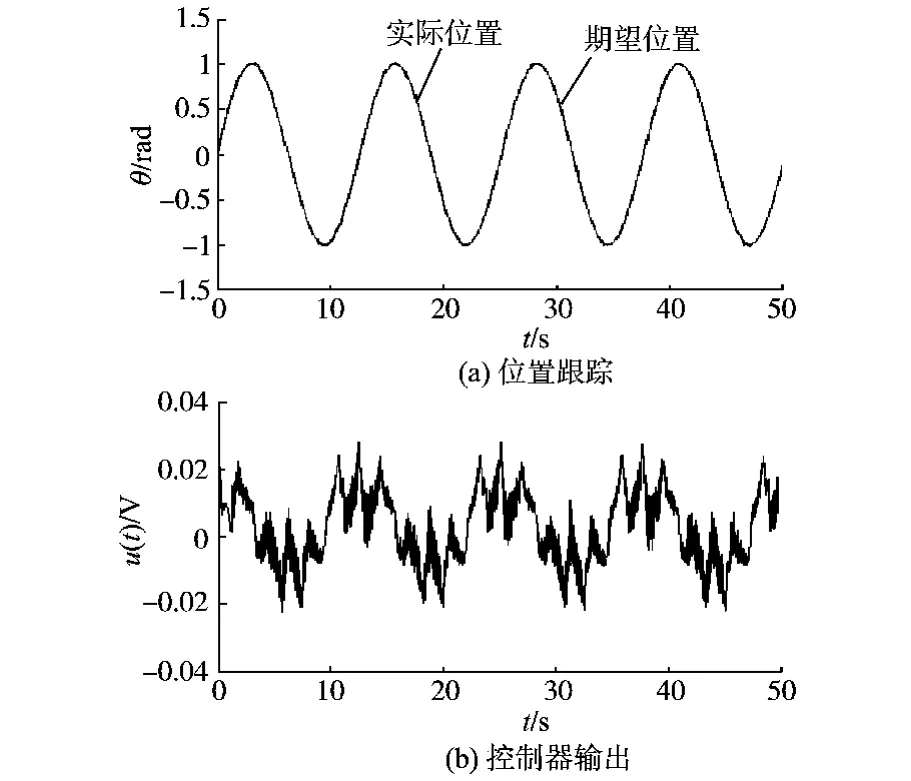
图6 SMC控制的实验结果Fig.6 Experimental results of SMC control

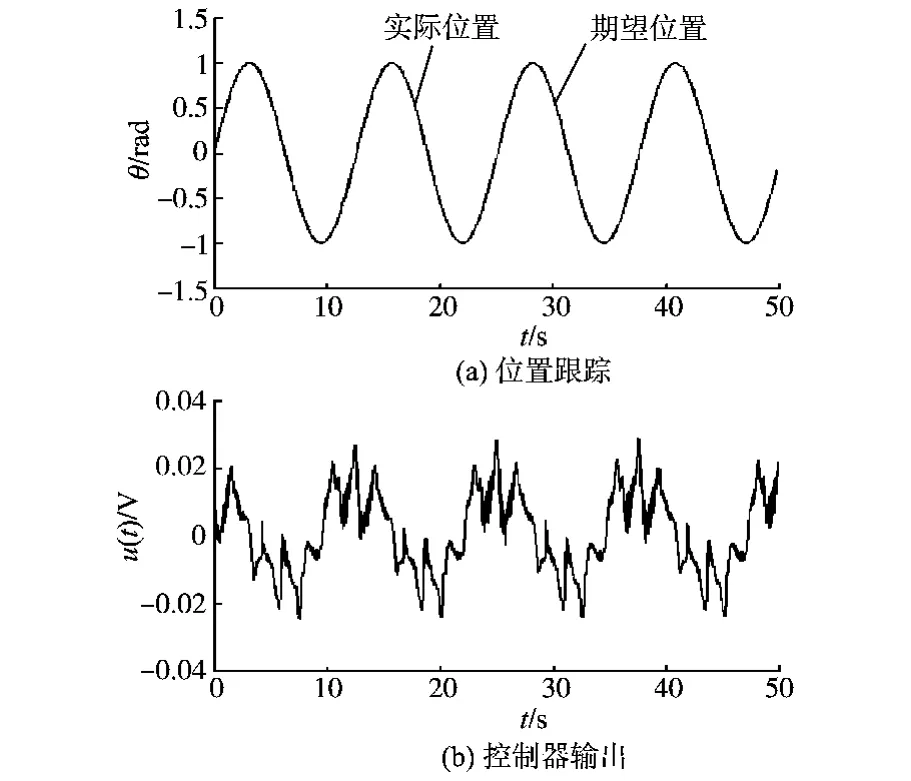
图7 ASMC＋I控制的实验结果Fig.7 Experimental results of ASMC＋I control

5 结论

本文提出位置伺服系统的一种自适应积分滑模控制方法，并理论证明其控制稳定性，并借助模块化伺服系统实验平台，开展控制实验研究。实验结果表明：相比传统的PID控制和滑模控制而言，该自适应积分滑模控制方法具有起控快、精度高、鲁棒性强等优点，且较好地削弱传统滑模控制器所固有的抖振效应。

［1］ 舒志兵.交流伺服运动控制系统［M］.北京：清华大学出版社，2006.

［2］ Jang J O，Jeon G j.A Parallel Neuro－controller for DC Motors Containing Nonlinear Friction［J］.Neruocomputing，2000，30（1）：233－248.

［3］ 高为炳.变结构控制的理论及设计方法［M］.北京：科学出版社，1998.

［4］ 王丰尧.滑模变结构控制［M］.北京：机械工业出版社，1994.

［5］ Ha Q P，Nguyen Q H，Rye D C，etal.Fuzzy Sliding Mode Controllers with Applications［J］.IEEE Trans.Ind.Electron，2001，48（1）：38－46.

［6］ Chen X K.Adaptive Sliding Mode Control for Discrete－time Multi－input Multi－output Systems［J］.Automatics，2006，42（3）：427－435.

［7］ Wang J，Rad A B，Chan P T.Indirect Adaptive Fuzzy Sliding Mode Control：Part I：Fuzzy Switching［J］.Fuzzy Sets and Systems，2001，122（1）：21－30.

［8］ Huang S J，Huang K S，Chiou K C.Development and Application of a Novel Radial Basis Function Sliding Mode Controller［J］.Mechatronics，2003，13（4）：313－329.

［9］ Boiko I，Fridman L，Iriarte R，etal.Parameter Tuning of Second－order Sliding Mode Controllers for Linear Plants with Dynamic Actuators［J］.Automatica，2006，42（5）：833－839.

［10］Eker I.Sliding Mode Control with PID Sliding Surface and Experimental Application to an Electromechanical Plant［J］.ISA Trans.，2006，45（1）：109－118.

［11］Li G.Robust Control Strategies for Motor Servo Systems Ph.D.Thesis［D］.Hong Kong：The Hong Kong Polytechnic University，1999.

修改稿日期：2011－12－25