离散傅里叶级数的抽样定理解释

李相国，梁义涛，李红岩

(河南工业大学信息科学与工程学院，河南郑州 450001)

离散傅里叶级数DFS及离散傅里叶变换DFT是“数字信号处理”课程中非常重要的内容之一。而且，离散周期信号的DFS是有限长(非周期)数字信号通过DFT计算离散谱的理论基础。因此理解DFS是理解DFT的前提与基础。本文分析了几种被广泛使用的国内外优秀教材及参考书，学习并比较了它们对DFS及DFT的处理方法。在学习借鉴基础上，从频域采样角度及采样定理的基本思路出发，推导了频域采样需要满足的条件，还给出了类似于频谱周期延拓的图形表达方式，它比公式表达更直观，有助于学生对DFS及DFT的感性认识。

1 现有的DFS定义

从数字信号处理的应用角度，一般面对的都是有限长(非周期)信号，因此，在引入离散周期信号时，普遍采用人为构造的方式。这样可以和已学知识建立联系以便更容易接受，也为进一步理解离散非周期信号的DFT做好了铺垫。

1.1 直接定义离散周期信号

在介绍DFS概念时，一些教材采用直接定义离散周期信号的方式［1-3］。这种方式偏重于数学推导，下面以著作［1］为例进行介绍。

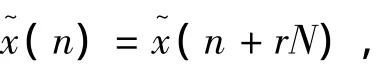
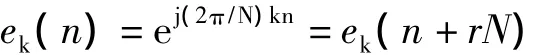
在此基础上，给出了其傅里叶级数的表达式:

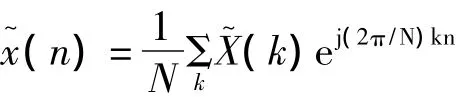
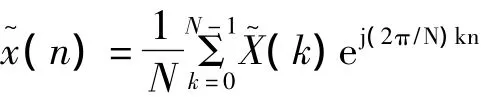
1.2 连续周期信号的时域采样

1.3 离散非周期信号的频域采样

在文献［5］和［6］中，都是从离散非周期信号的连续周期谱的采样开始。但其后续处理方式并不一样。在文献［5］中采用了如下处理方式。

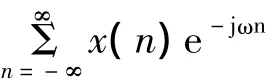
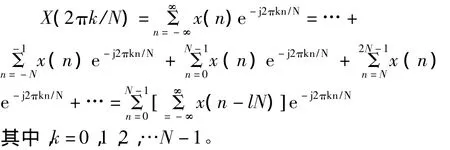
文献［6］中的频域采样在一个周期内进行，得到的是一个有限长的(非周期)离散谱，因此，其没有使用离散周期信号以及DFS，而是直接给出了DFT表达式。

2 基于频域采样法的DFS定义

我们注意到，文献［7］从离散时间信号的卷积定理角度解释频域采样。受到该思路以及傅里叶变换性质中对偶性的启发，本文沿着采样定理的思路，证明频域采样需要满足的条件，我们在最后还给出图形解释。

2.1 离散非周期信号频谱的“频谱”

因此，上述表达式可简化为Y(jm)=x(-m)。也就是说，一个离散时间信号x(n)的频谱X(ejω)的频谱Y(jm)是其时域表达式的反转x(－m)，如图1所示。

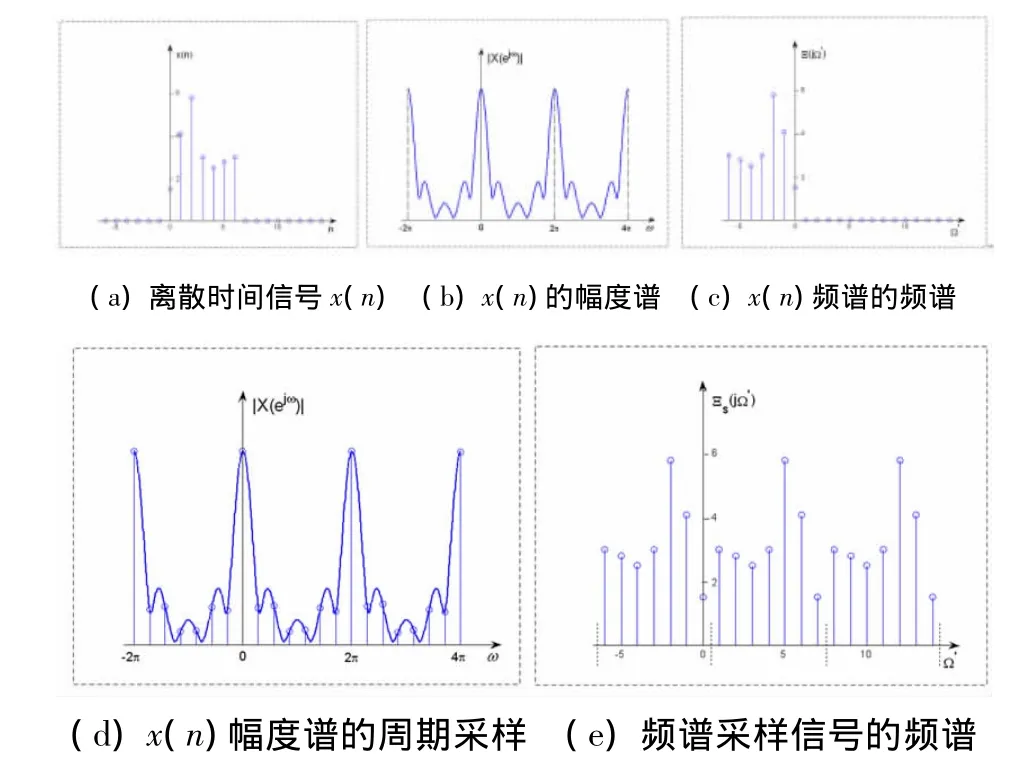
图1 离散时间信号频域采样的采样关系示意图

2.2 DFS的采样定理解释

参照 Nyquist采样定理的思路［4］，接下来证明对连续信号X(ejω)进行频谱无失真周期采样需要满足的条件。

设以ωs为周期对X(ejω)进行采样得到离散信号Xs(jkωs)，k取全部整数。这可解释为X(ejω)与单位冲激串函数p(ω)的相乘，即

从上式可知，对X(ejω)进行周期采样得到离散信号Xs(jkωs)，其频谱表达式等于x(n)反转后的周期延拓，延拓周期等于Ω's，如图1中所示。

当x(n)是长度为N的有限长信号时，只要满足Ω's＞N－1就可避免频谱混叠，可以实现频谱无失真的周期采样。我们取Ω's的值为满足条件的最小整数Ω's=N，则时域采样周期ωs=2π/N。此时的Xs(jkωs)也是周期的，简化记作(k):

上面我们完成了从采样定理角度对频域采样的图形化解释与推导。

3 结语

本文从频域采样与采样定理的角度出发解释DFS，得出了频域无失真采样需要满足的条件，并给出了类似于频谱周期延拓的图形表达方式。该方法的优点是其图形表示更直观，有助于增加感性认识;其缺点是数学推导比较繁琐，容易混淆。

形象化教学是提高教学效果的一种有效方法，因此，把本文的图形化方法作为辅助手段，配合前述各种方法使用，期望能够提高学生的学习兴趣及教学效果。

［1］Oppenheim A.V.，Schafer R.W.，Buck J.R.Discrete-Time Signal Processing［M］.2nd ed.Prentice Hall，1999

［2］Antoniou A.Digital Signal Processing:Signals，Systems，and Filters［M］.McGraw-Hill，2005

［3］程佩青.数字信号处理教程［M］.第二版.北京:清华大学出版社，2002

［4］胡广书.数字信号处理导论［M］.北京:清华大学出版社，2005

［5］Proakis J.G.，Manolakis D.K.Digital Signal Processing:Principles，Algorithms and Applications［M］.3rd ed.Prentice Hall，1995

［6］Mitra S.K.Digital Signal Processing:A Computer-Based Approach［M］.2nd ed.McGraw-Hill，2001

［7］Diniz P.S.R.，Silva E A.B.D.，Netto S.L.Digital Signal Processing:System Analysis and Design［M］.2nd ed.Cambridge University Press，2010