混合式双级矩阵变换器的改进与优化

李生民，闫晓飞，钟彦儒

（西安理工大学自动化与信息工程学院，西安 710048）

双级矩阵变换器TSMC（two stage matrix converter）是一种新型“全硅”功率变换器，近年来受到学者的广泛关注［1］。与传统交－直－交变换器相比，双级矩阵变换器的输入输出特性良好、功率因数可调且无需大的储能元件；同时相对于常规矩阵变换器，双级矩阵变换器的换流策略更加安全可靠，箝位电路简单且在特定约束条件下可进一步减少电力电子器件数量。此外双级矩阵变换器在多驱动系统中还可实现多个逆变级共享同一个整流级［2～5］。

受控制策略的影响，电压传输比低（仅为0.866）仍然是双级矩阵变换器亟待解决的问题之一［6］。目前提高电压传输比一般有两种途径：一种是改进调制算法，如文献［7］将逆变器过调制策略引入双级矩阵变换器，该调制策略的电压传输比最大可达0.955，但其控制算法复杂且输出谐波过大；另一种是改进电路拓扑结构，如文献［8］提出的高频母线矩阵变换器，但高频变压器的加入使变换器的结构、控制策略和设计都变得十分复杂。

文献［9］提出了混合式双级矩阵变换器。这种拓扑结构是在双级矩阵变换器直流环节串联一个升压（BOOST）变换器。这虽然增加了带电容的升压电路，但电容很小，不会影响整个变换器的体积。该拓扑通过控制升压变换器，使逆变级的输入电压提高，从而达到提高其电压传输比的目的。相比普通双级矩阵变换器，这种拓扑结构具有电压传输比高、无需添加箝位电路等特点。但它仍存在拓扑结构与调制策略复杂，直流环节电压波动剧烈，输出波形谐波很大等问题。

为了解决上述问题，本文对混合式双级矩阵变换器的拓扑结构进行了改进，使其控制更为简单；同时提出一种带前馈补偿的空间矢量脉宽调制策略以改善输出波形质量。

1 混合式双级矩阵变换器原理

1.1 混合式双级矩阵变换器

混合式双级矩阵变换器拓扑结构如图1所示，整流级和逆变级的拓扑都和普通双级矩阵变换器相同，在中间直流环节中，增加了升压电路，通过控制T1、T2、T3和T4四个开关，提升直流母线电压。当变换器能量正向流动时，断开，其中第一阶段，T2、T4闭合，T2断开，电感L储能，电容C为逆变侧供电；第二阶段，T2、T3闭合，T4断开，整流侧给逆变侧供电，同时为电容C充电。当变换器能量反向流动时，T1闭合，T2断开，将升压电路短接，同时，T3、T4闭合，电容、电感中的能量释放。

这种拓扑可以很好地提高电压传输比，但升压电路需要同时控制四个开关，控制难度较大，需要将拓扑进一步改进。

图1 混合式双级矩阵变换器拓扑结构Fig.1 Topology structure of hybrid two－stage matrix converter

1.2 改进的混合式双级矩阵变换器

改进的混合式双级矩阵变换器拓扑结构如图2所示，可分为整流、升压和逆变三部分。整流部分同传统双级矩阵变换器相同，由6个双向开关构成，将三相输入电压Va、Vb、Vc转化成高频脉冲直流电压Vdc。升压电路将Vdc电压幅值升高，起到提高电压传输比的作用，提升的幅值可以通过选择适当的升压电路占空比调节。这个过程中需要控制的只有开关管T。开关管T1以及二极管D1用于能量反向流动。当能量反向流动时，打开T1，将升压电路短接，并且将电容C和电感L上存储的能量释放掉。逆变部分由6个IGBT构成常规的电压型逆变器。为了在线性范围内提高电压传输比并且改善波形质量，本文在逆变部分采用空间矢量脉宽调制（SVPWM）控制算法。

图2 改进混合式双级矩阵变换器拓扑结构Fig.2 Topology structure of improved hybrid two－stage matrix converter

2 调制策略

2.1 整流部分调制策略

为了简化分析，假设网侧没有输入滤波器，采用理想的三相电压作为输入，即

式中：Uim为输入电压的幅值；ωim为输入角频率；θa、θb、θc为输入电压相位角。输入电压波形如图3所示。

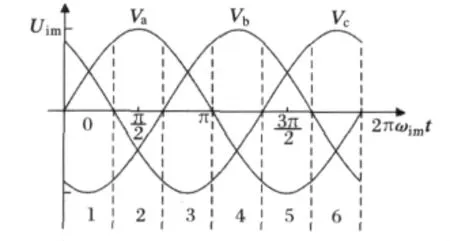
图3 三相输入电压波形及扇区划分Fig.3 Input three－phase voltage waveforms and the vectors demarcation

三相输入电压连续两个零点之间相隔60°，在每个60°区域中一相电压幅值的绝对值最大，其他两相电压极性与之相反，按此原则将输入电压划分为6个扇区。每个脉宽调制（PWM）周期分为两段，依次输出相应的两个最大且极性为正的线电压，因此，整流级在一个PWM周期内只产生两个有效空间矢量，而不会出现零矢量。

以扇区2为例，此时在一个开关周期中直流电压分别为线电压Uab和Ubc，它们对应的两个时间段占空比为

一个PWM周期内的局部平均直流电压为

将式（3）代入式（1）和式（2），可得

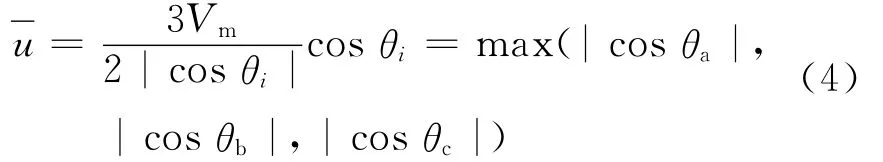
依此类推，可以得出其余5个区间的开关状态和直流电压。

2.2 升压部分调制策略

升压电路输入电压Ud由两个不同的线电压合成，当设置升压电路开关管T频率足够高时，可以将每一个PWM周期的输入电压看作一个波动不大的直流恒定电压输入。因此，升压电路采用常见的直流升压电路控制方法，通过控制升压开关T的通断，发挥升压电感L的电压泵升作用，将直流母线电压抬升。限于篇幅，本文对此不再赘述。

2.3 逆变部分调制策略

逆变部分的拓扑结构与常规的电压源逆变器相同，控制算法采用SVPWM。SVPWM策略中一共有8种允许的开关组合，每种开关组合对应一个空间矢量，8个空间矢量可分为6个非零矢量和2个零矢量。非零空间矢量幅值相等，相位依次互差60°，构成一个正六边形，如图4（a）所示。非零矢量将坐标平面等分成6个扇区。利用Park变换将三相瞬时输出电压映射成坐标平面的空间电压矢量任意时刻落在六边形中的某一扇区中，可由该扇区的两个非零矢量Uα和Uβ和一个零矢量U0合成而得到，输出相电压空间矢量的合成原理图如图4（b）所示。

各矢量的作用时间根据空间矢量调制原理和正弦定理计算得到：

即得到

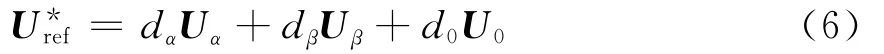
式中：Ts为采样周期；m为空间矢量脉宽调制系数；Tα、Tβ、T0分别为Uα、Uβ和U0在一个采样周期中的作用时间。

图4 空间矢量合成图Fig.4 Composition graph of space vector

SVPWM与常规的正弦脉宽调制（SPWM）相比不仅提高了直流电压利用率和动态响速度，降低了输出波形中所含谐波含量，而且更易于数字化实现。

2.4 电压传输比分析

对于常规双级矩阵变换器，假设输入电压处于第一扇区，输出线电压矢量也处于第一扇区，则三相输出线电压在一个PWM周期内的平均值为

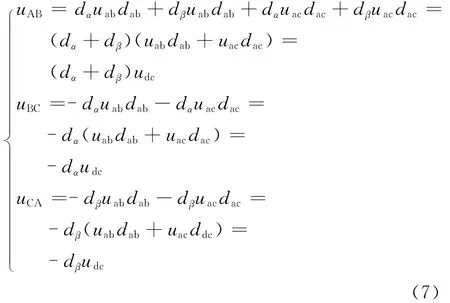
将式（4）和式（5）代入式（7）得

式中，UOM为输出相电压幅值φi。TSMC的电压传输比为

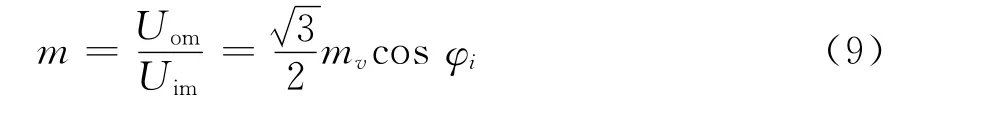
当cosφi＝1且mv＝1，电压传输比达到最大值为0.866。

BOOST电路处于稳态工作时，其输出电压Uom＝T／toffUim＝（1－d）Uim，因此，其电压传输比为

式中，d为BOOST电路占空比。

由式（9）和式（10）可得混合双级矩阵变换器电压传输比为

可见，随着d变化，矩阵变换器的电压传输比可以达到并超过1。

2.5 补偿环节

直流母线升压电路，不仅将直流母线电压大幅提升，也加剧了直流母线电压波动加剧。由于变换器中不含大功率储能元件，直流母线电压的波动无法消除，电压波动会直接对逆变部分输出波形造成影响，导致输出波形谐波畸变率增大，因此本系统在逆变部分加入了补偿环节补偿直流母线电压波动。

控制器实时采集直流母线电压值Vdc，与期望的直流母线电压相比较，对空间矢量脉宽调制系数m进行实时补偿。补偿后的调制系数为

当直流电压Vdc减小时，补偿算法使空间矢量调制系数变大，增加开关管开通时间以补偿电压减小造成的影响；当直流电压Vdc增大时，补偿算法使空间矢量调制系数减小，减少开关管开通时间以补偿电压增大造成的影响，保持系统输出稳定，减小输出波形的谐波含量。

3 仿真研究

本文在Matlab 6.5仿真环境下，利用simulink模块和m－function模块建立了混合双级矩阵变换器的仿真模型。系统参数如下所示：开关调制频率fs为5 k Hz，输入三相电压源相电压幅值为×220 V，频率为50 Hz，负载为星型连接的RL负载，R＝10Ω，L＝1 m H。升压电路参数为：电感L＝1μH，电容C＝1μF，开关频率f＝40 k Hz，占空比d＝0.156。

图5（b）为经过升压电路抬升后的直流母线电压，可见直流母线电压幅值得到较大的提高，但波形具有很大的波动。

在采用相同参数情况下，将普通双级矩阵变换器与混合式双级矩阵变换器的输出波形进行比较。设置期望输出电压频率80 Hz，期望直流母线电压设为538.8 V，空间矢量脉宽调制系数m设为1。

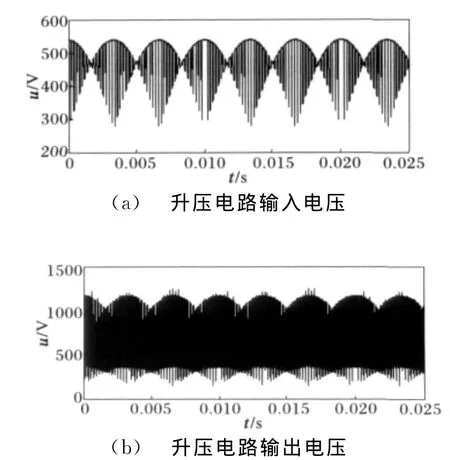
图5 混合双级矩阵变换器直流母线电压Fig.5 DC－bus voltage waveform＇s of hybrid two－stage matrix converter

图6为普通双级矩阵变换器输出相电压波形，电压基波幅值为269.4，总谐波畸变率（THD）为0.86%。图7混合式双级矩阵变换器输出相电压波形，电流基波幅值为315.4 V，THD为2.54%。可见，混合式双级矩阵变换器有效的提高了输出电压幅值，但其输出电压谐波含量也同时增加。

图6 普通双级矩阵变换器输出相电压波形Fig.6 Output voltage waveform of two－stage matrix converter

图7 混合式双级矩阵变换器输出相电压波形Fig.7 Output voltage waveform of hybrid two－stage matrix converter

图8为带有补偿环节控制系统的混合式双级矩阵变换器输出相电压波形，基波幅值为311.1 V，THD为1.72%。与图7相比，可以看出补偿后输出电压幅值稳定，谐波含量降低，表明该前馈补偿算法是有效的。

图8 带有补偿环节控制系统的混合式双级矩阵变换器输出相电压波形Fig.8 Output phase voltage waveform of hybrid two－stage matrix converter with feed－forward compensation

图9为带补偿环节的混合式双级矩阵变换器输出线电压波形，基波幅值为538.9 V，THD为1.77%。电压幅值与输入线电压幅值相同，电压传输比达到1。如果增大升压电路占空比，可进一步提高输出电压的幅值，使电压传输比超过1。

图9 带有补偿环节控制系统的混合式双级矩阵变换器输出线电压波形Fig.9 Output line voltage waveform of hybrid two－stage matrix converter with feed－forward compensation

4 结语

本文针对混合式双级矩阵变换器拓扑复杂、输出谐波较大的问题，对其结构进行了改进，并提出了一种具有补偿环节的SVPWM控制策略，改善波形质量。采用Matlab建立了该系统仿真模型并对控制策略进行仿真。结果表明，本文所提出的控制策略可以有效减少输出波形的谐波含量，使输出电压波形具有良好的正弦度。同时验证了改进的混合式双级矩阵变换器可以提高电压传输比，其输出电压频率、幅值皆连续可调，并且控制算法简单，作为一种新型拓扑结构具有一定的研究价值。

［1］ 陈伯时（Chen Boshi）.矩阵变换器的发展与展望（The development and prospect of matrix converter）［J］.电工技术杂志（Electrotechnical Journal），2003，2（10）：4－5.

［2］ Wei L，Lipo T A.A novel matrix converter topology with simple commutation［C］∥Industry Applications Society Annual Meeting.Chicago USA：2001.

［3］ 令狐文娟，邓文浪，朱建林，等（Linghu Wenjuan，Deng Wenlang，Zhu Jianlin，et al）.双级矩阵变换器的自抗扰闭环控制（Closed－loop control of two－stage matrix converter based on auto－disturbance rejection controller）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2008，20（2）：98－104.

［4］ 粟梅，马进，孙尧，等（Shu Mei，Ma Jin，Sun Yao，et al）.基于双级矩阵变换器的线间潮流控制器（Interline power flow controller based on two－stage matrix converter）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2008，20（6）：17－21.

［5］ 王勇，文辉清，吕征宇，等（Wang Yong，Wen Huiqing，LüZhengyu，et al）.基于MATLAB的矩阵变换器空间相量调制研究（Research on space vector modulation strategy of matrix converter based on Matlab）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2004，16（5）：14－19.

［6］ 邓文浪，杨欣荣，朱建林，等（Deng Wenlang，Yang Xinrong，Zhu Jianlin，et al）.18开关双级矩阵变换器的空间矢量调制策略及其仿真研究（Space vector modulation strategy of two－stage matrix converter with 18 switches and it＇s simulation study）［J］.中国电机工程学报（Proceedings of the CSEE），2005，25（15）：84－90.

［7］ Li Zhiyong，Cai Hao，Li Xiaoying，et al.Voltage transfer characteristic analysis of dual－bridge matrix converter［C］∥Conference on Intelligent Computation Technology and Automation.Changsha，China：2008.

［8］ Cha Han Ju，Enjeti Prasad N.A three－phase AC／AC high－frequency link matrix converter for VSCF applications［C］∥IEEE Annual Power Electronics Specialists Conference.Acapulco，USA：2003.

［9］ Mariethoz S，Wijekoont T，Wheeler P.Analysis，control and comparison of hybrid two－stage matrix converters for increased voltage transfer ratio and unity power factor［C］∥Fourth Power Conversion Conference.Nagoya，Japan：2007.