输电线路分布式行波检测的故障定位方法

徐湘忆，盛戈皞，刘亚东，江秀臣

（上海交通大学电子信息与电气工程学院，上海 200240）

输电线路发生故障后，故障点将产生沿线路向两端运行的暂态行波。由于波阻抗不连续，行波在故障点、故障线路母线及与故障线路相连接的其它线路末端母线会发生折射和反射［1］。利用暂态行波所包含的故障信息，理论上可以实现精确故障定位。目前主要的行波测距算法大多是通过在变电站电压电流互感器二次侧（低压侧）安装行波检测装置，运用基于单端法或双端法的各种定位算法来完成故障测距［2］。

综合分析现有行波测距算法可知，波头到达时间和行波波速是影响测距精度的两大主要因素［3］。目前，利用GPS（global positioning system，全球定位系统）的高精度授时功能和小波变换分析技术，理论上可以精确定位行波波头的到达时间，但由于传统互感器高频特性较差，装置采样频率有限等问题，多数测距算法的原理性误差较大。此外，针对行波波速的确定，绝大多数算法并没有考虑如何在线测量故障瞬间的实时行波波速，而是采用了直接应用经验值、参考值或参数估算等方法。由于影响行波波速的因素诸多，若不能精确求取实时行波波速，将会影响故障测距的精度，降低定位的可靠性［4］。

针对上述问题，本文基于可安装在高压侧的输电线路行波检测装置，准确获取线模初始行波和反射波到达不同检测装置的时间，并充分利用不同的波头时差信息，在线测量实时行波波速，实现精确故障定位。

1 输电线路行波检测装置

本文采用的行波检测装置直接安装在高压输电线上，主要包括供电模块、行波提取模块、高速采样与存储模块、无线通信模块和GPS模块5部分，结构框图如图1所示。

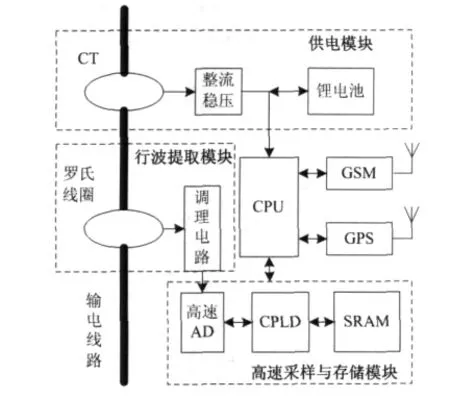
图1 装置结构Fig.1 Structure diagram of device

供电模块采用CT直接从高压输电线上感应取电，并配大容量锂电池作为备用电源。输电线路负荷电流较大时由CT取电模块直接给系统供电同时给备用电池充电，在输电线路发生短路故障或者负荷电流较小时备用电源可为系统提供能量支撑。该供电方式可确保输电线路没有负荷电流的情况下，模块依然能够稳定、可靠地为装置供电。

行波提取模块利用Rogowski线圈采集故障行波信号，由于Rogowski线圈具有高带宽、无饱和等特点，可消除传统互感器因带宽限制而引起行波信号发生畸变的情况［5，6］。

Rogowski线圈采集的行波信号经放大、滤波后送入高速采样与存储模块，该模块由CPLD（complex programmable logic device，复杂可编程逻辑器件）控制。一旦线路发生故障，CPLD即启动A／D进行高频采样，采样频率10 MHz，并将采样数据依次写入SRAM。采样完成后，CPLD即通知CPU，由CPU读取采样数据进行相模变换、小波变换等后续数据处理，检测行波波头并定位波头到达装置的时间。

无线通信模块负责将检测结果以GSM（global system for mobile communications，全球移动通讯系统）短消息的方式传回监控主站，主站接收到子节点的短消息后回发信号确认收到。如监控主站在设定时间内没有回发确认信号，子节点将重新发送检测结果至收到监控主站确认信号为止。此无线发送确认机制可保证检测数据在覆冰或电晕等现场运行环境较为恶劣的情况下可靠发送和接收。GPS模块提供检测装置采集数据的精确时间，并由GPS的时钟脉冲来同步采样时间，以实现异地同步采集。

考虑到装置的野外工作环境，外部结构采用双层屏蔽设计，并有密封防水处理，内部器件多选用军工级高性能元件，可有效防潮，抗电磁干扰、抗振动等，在较恶劣的自然环境和电磁环境中均能可靠稳定地工作。

2 行波波头的准确定位

2.1 相模变换

由于三相线路之间存在耦合，其电磁暂态过程通常不能孤立地看成相互独立的单根导线上的电磁暂态过程，因此，一般都采用相模变换进行解耦。本文采用文献［7］提出的一种新的相模变换矩阵，弥补了Clarke、Karenbauer等几种常用变换矩阵的不足之处，实现了单模量反映所有故障类型的目的。变换公式为

采用上述变换后，在任何故障类型下，1模和2模均存在，可任选其一进行小波分析，提取故障信息。

2.2 利用小波变换检测行波波头

小波变换具有时频局部化特性，适合对行波这类非平稳变化信号进行分析。当采用二进小波变换时，尺度参数以2的倍数增大，频带以2的倍数降低，可实现信号的无重叠全频分解，每一尺度的小波变换结果就是信号在对应频带的分量［8］。由于篇幅有限，二进小波算法不再赘述，具体公式可参考文献［9］。

由于小波变换的模极大值对应于信号的奇异点，因而可利用小波变换准确识别行波波头。小波模极大值的定义如下［10］。

WSf（x）是函数f（x）的小波变换，在尺度S下，若在x0的某一领域，对一切x∈（x0－δ，x0＋δ），有｜WSf（x）｜≤｜WSf（x0）｜，则x0为小波变换的模极大值点，WSf（x0）为模极大值。

本文采用10 MHz的采样频率，引入了大量的高频噪声信号，又行波的特征频带一般在几百千赫兹以内，故可舍弃尺度1和尺度2，采用尺度3下的小波变换来分析线模信号。图2所示即为尺度3下的小波变换，可以看出，线模初始行波和反射波的波头（第一、第二个波头）所对应的模极大值很明显，故可利用线模第一、第二个波头进行故障测距。

图2 尺度3下的小波变换Fig.2 Result of wavelet transformation under scale 3

3 故障定位方法的实现

3.1 定位系统的基本构成

本文所述的故障定位系统由两套安装在输电线上的行波检测装置和一个监控主站构成，如图3所示。

输电线路行波检测装置的具体安装方法如下。

（1）以线路某一端变电站的母线为参考端，如母线M。

当线路F点处发生故障时，故障点会同时产生向线路两端传播的暂态行波，各检测装置按照预先设定的越限触发功能进行启动，采集故障电流行波，并进行相模转换和小波变换，准确识别线模第一、第二个波头，并将两个波头到达装置的时间信息回传主站。

图3 故障定位系统Fig.3 Fault location system

3.2 故障区段的判定

主站收集到装置A、B分别传回的线模第一、第二个波头时间信息tA、t′A、tB、t′B后，首先要确定故障点所在的区段，方法如下。

1）求取时间阈值τ。

先根据线路参数估算线模波速v′，即

式中，L1，C1分别为单位长度线路的正序电感和正序电容［11］。

由估算值v′求取时间阈值τ，即

2）根据装置传回主站的波头时间信息，计算以下各种波头时差。

到达装置A、B的线模第一个波头时差tAB＝tA－tB；到达装置A的线模第一、第二个波头时差tA′A＝tA′－tA；到达装置B的线模第一、第二个波头时差tB′B＝tB′－tB。

3）比较时差tAB与时间阈值τ的大小，判定故障区段。

①若｜tAB｜≤τ，则故障位于区段2；

②若｜tAB｜＞τ且tAB＜0，则故障位于区段1；

③若｜tAB｜＞τ且tAB＞0，则故障位于区段3。

3.3 实时行波波速的测量

若知道了故障点所在的故障区段，则可根据不同的区段，在线测量实时行波波速。

若故障点位于区段1，则故障点产生的向N端传播的行波将依次经过装置A、B，如图4（a）所示。由到达两个装置的线模第一个波头时差即可求出实时波速同理，故障点位于区段3时，亦可由时差tAB得到实时波速

若故障点位于区段2，如图4（b）所示，则理论上应满足

考虑到由于检测装置实际采样精度等造成的原理性误差，可综合tA′A、tB′B求取实时行波波速为

图4 行波折反射图Fig.4 Refraction and reflection of traveling wave

3.4 故障距离的求取

根据故障区段的判定结果和相应测得的实时行波波速，可求出故障点到参考端的故障距离dc如下。

4 EMTP仿真实验

为验证方法的正确性，采用EMTP仿真软件对图3所示500 k V双端电源系统进行仿真。

线路全长150 km，以母线M为参考端，在距离参考端50 km处和100 km处的输电线上分别安装行波检测装置A、B，将整条线路3等分。线路参数为：R1＝0.02Ω／km，R0＝0.3Ω／km；L1＝0.9 m H／km，L0＝3 m H／km；C1＝0.0127μF／km，L0＝0.0077μF／km。

为求时间阈值，先由线路参数L1、C1，估算线模波速时间阈值

设定距参考端80 km处发生故障，故障初相角为45°，过渡电阻为100Ω，采样频率为10 MHz。装置A、B各自采集故障电流行波，经相模转换和小波变换得到线模第一、第二个波头到达时间tA、tA、tB、tB′详见表1。

表1 线模第一、第二个波头到达两装置时间Tab.1 Arrival times of the first and second aerial mode traveling wave at both detectors μs

根据故障区段的判定方法，由｜tAB｜≤τ，可先判定故障点位于区段2，并可求得实时行波波速为

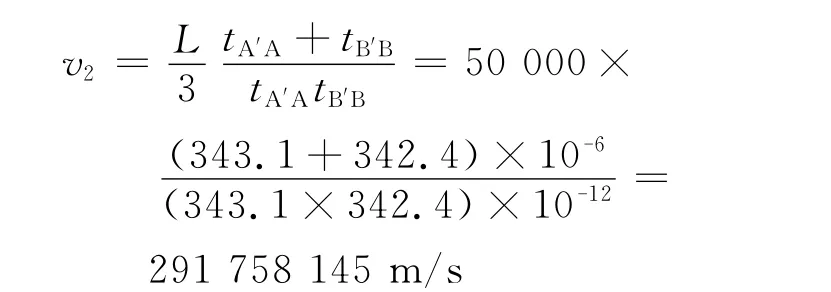
最后计算故障点F到参考端的故障距离dc为

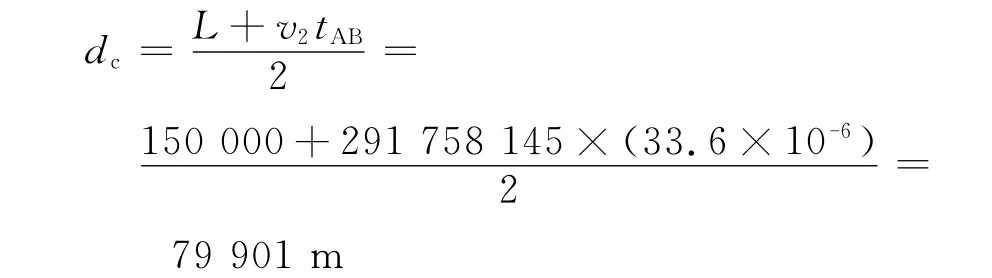
绝对误差为－99 m，测距精度较高。

表2为各种测距结果汇总。可以看出，在不同的故障位置，经不同的过渡电阻，于不同的故障初相角发生故障，采用本文方法均可有效定位故障点，且测距精度较高。

表2 测距结果Tab.2 Fault location Results

此外，由表2中的数据也可看出，临近检测装置处发生故障，会对波头的定位稍有影响，导致误差略有增加，最大误差为279 m，但依然可以满足现场要求。

5 结语

本文详细介绍了基于输电线路分布式行波检测装置的故障定位方法，通过选择合适的尺度对线模行波进行小波变换，并采用模极大值法检测行波波头，能准确定位波头到达时间。主站利用不同的波头时差信息，在线测量实时行波波速，可精确定位单条输电线路的故障。仿真结果表明：针对不同的故障位置，本文方法均能准确定位故障点，且有效抑制了过渡电阻、故障初相角等因素的影响，可靠性高，测距精度能够较好地满足现场故障定位的要求。

［1］ 刘巍，湛大千（Liu Wei，Zhan Daqian）.基于反向行波的故障测距（Fault location method based on backward traveling wave）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2006，18（5）：62－65.

［2］ 葛耀中，徐丙垠，陈平（Ge Yaozhong，Xu Bingyin，Chen Ping）.利用暂态行波测距的研究（Study of fault location based on traveling waves）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），1996，8（3）：17－22.

［3］ 覃剑，葛维春，邱金辉，等（Qin Jian，Ge Weichun，Qiu Jinhui，et al）.输电线路单端行波测距法和双端行波测距法的对比（Study on single terminal method and double terminal method of traveling wave fault location in transmission line）［J］.电力系统自动化（Automation of Electric Power Systems），2006，30（6）：92－95.

［4］ 黄雄，王志华，尹项根，等（Huang Xiong，Wang Zhihua，Yin Xianggen，et al）.高压输电线路行波测距的行波波速确定方法（Traveling wave velocity measurement in fault location based on traveling wave for high voltage transmission line）［J］.电网技术（Power System Technology），2004，28（19）：34－37.

［5］ 邹积岩，段雄英，张铁（Zou Jiyan，Duan Xiongying，Zhang Tie）.罗柯夫斯基线圈测量电流的仿真计算及实验研究（The simulating calculation and experimental research of Rogowski coil for current measurement）［J］.电工技术学报（Transactions of China Electrotechnical Society），2001，16（1）：81－84.

［6］ 刘孝先，曾清，邹晓莉，等（Liu Xiaoxian，Zeng Qing，Zou Xiaoli，et al）.电子式互感器的应用（Application of electronic transformer）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2010，22（1）：133－137.

［7］ 宋国兵，李森，康小宁，等（Song Guobing，Li Sen，Kang Xiaoning，et al）.一种新相模变换矩阵（A novel phase－mode transformation matrix）［J］.电力系统自动化（Automation of Electric Power Systems），2007，31（14）：57－60.

［8］ 葛耀中.新型继电保护和故障测距的原理与技术［M］.2版.西安：西安交通大学出版社，2007.

［9］ 唐晓初.小波分析及其应用［M］.重庆：重庆大学出版社，2006.

［10］郑州，吕艳萍，王杰，等（Zheng Zhou，LüYanping，Wang Jie，et al）.基于小波变换的双端行波测距新方法（A new two－terminal traveling wave fault location method based on wavelet transform）［J］.电网技术（Power System Technology），2010，34（1）：203－207.

［11］刘笙.电气工程基础：下册［M］.北京：科学出版社，2002.