参照系统负荷预测的母线负荷预测修正方法

杨理才，贺 辉，刘国特，姚建刚

（1.湖南大学电气与信息工程学院，长沙 410082；2.湖南省电力调度通信局，长沙 410007）

电力系统负荷预测分为系统负荷预测与母线负荷预测。系统负荷预测以一个地区的总负荷为预测对象，而母线负荷可以定义为由变电站的主变压器供给一个相对较小的供电区域的终端负荷的总和，是系统负荷的细化［1］。目前常用基于母线负荷自身变化规律的预测方法，通过分析各母线的负荷规律来预测自身负荷，然后对照系统负荷进行修正［2］。目前针对如何参照系统负荷预测值修正母线负荷的研究尚少，本文提出了一种切实可行的方法。

系统负荷预测［3～6］基数大，气象等信息更加齐备，因此预测准确率相对更高。母线负荷基数小，干扰对母线负荷值的相对影响更大，由于干扰产生的误差累积效应导致了母线负荷预测值之和作为系统负荷预测值要比系统负荷预测值的准确率低，利用系统负荷预测值来修正母线负荷预测值，是提高母线负荷预测准确率的一种切实可行的途径，而目前对母线负荷预测的研究主要集中在系统开发方面［7～9］。

本文根据母线负荷预测值之和与系统负荷预测之间的差值，提出了一种修正母线负荷预测值的方法。该方法通过分析在系统负荷相似的历史时刻母线负荷的分布规律，得出母线负荷修正后的分布范围，在该范围内求出最优修正方案，采用最小二乘逼近，利用LINGO（linear interactive and general optimizer）软件求解该二次规划问题，算例表明了该修正方法的可行性。

1 母线负荷与系统负荷

母线负荷是系统负荷的细化，以湖南某市为例，该市的负荷为所辖的24条220 k V母线负荷的总和，包括19条公用母线负荷和5条高铁专用母线负荷，以15 min为采样周期，从00：00－23：45对各母线日负荷进行采样，得到的96点日负荷曲线如图1所示，图中各细线为母线负荷曲线，粗线为母线的平均负荷曲线，该平均负荷是系统负荷的1／24，反映了系统负荷的变化趋势。

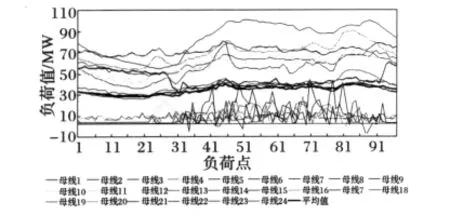
图1 母线负荷Fig.1 Bus load

式中：Φe为日平均预报准确率；Lf，k为第k点的预测值；n为参与计算准确率的负荷点数；Lh，k为该日第k点的实际值；Lb，k为第k点的负荷基准值，此处取该时刻的实际值。图中系统负荷预测的准确率为96.1%，而母线负荷预测之和的准确率为94.8%。系统负荷预测相对于母线负荷预测之和的准确率

将某日各母线负荷预测之和、系统负荷预测值分别与系统负荷实际值进行对比，如图2所示，从图中可以看出系统负荷预测值更加接近于系统负荷实际值，分别计算它们的准确率，计算公式为较高，原因有以下三点：

（1）系统负荷基数大，规律容易把握，母线负荷基数小，单个母线负荷预测的准确率低；

（2）母线负荷供电范围小，一般缺乏当地精确的气象预报，而是以系统负荷预测采用的气象预报为准；

（3）系统负荷预测值只进行一次预测，母线负荷预测需进行多次，可能导致误差累积。

对母线负荷修正时，需要根据各母线的负荷规律分别修正。如图1所示，各母线负荷基数各不相等，且增长方向并不都与系统负荷的增长趋势相同，所以相对系统负荷预测值进行修正时，各母线负荷的修正值与修正方向各不相同。

图2 母线负荷预测之和与系统负荷预测准确率对比Fig.2 Accuracy contrast of sum of bus load forecasting and system load forecasting

2 修正方法

记系统负荷预测L，母线负荷为P；下标his表示历史负荷，下标for表示预测负荷，sum表示母线负荷之和；n表示采样的负荷总点数，m为母线的总数，d为相似日天数。

2.1 修正的条件

在Psum，for超出了Lfor一定比值需要对Pfor进行修正，称这个比值为负荷的可靠率δ，取为系统负荷在该季节内的平均系统负荷预测准确率，令

式中，k为修正系数，0＜k≤1，一般取k＝1，若无最优修正解，则适当减少值，使得负荷的可信区间增大。

对母线负荷分时间点进行分析，如果该点的母线负荷预测值之和满足

则认为该点的母线负荷预测值之和是可靠的，同样各母线的负荷预测值也是可靠的，否则，该时刻的母线负荷需要修正。

2.2 修正方法

2.2.1 相似曲线与相似日

对Psum，for不满足式（3）的点进行修正，先找相似日，把母线负荷的相似日转变为求系统负荷的相似日。由于单个负荷点无法反映负荷的变化趋势，因此取该负荷点的前后若干时间段的负荷组成负荷曲线。找该时间段的系统负荷的相似曲线［10］，通过计算系统负荷预测曲线与历史曲线的相似程度与欧氏距离来寻找相似日，即

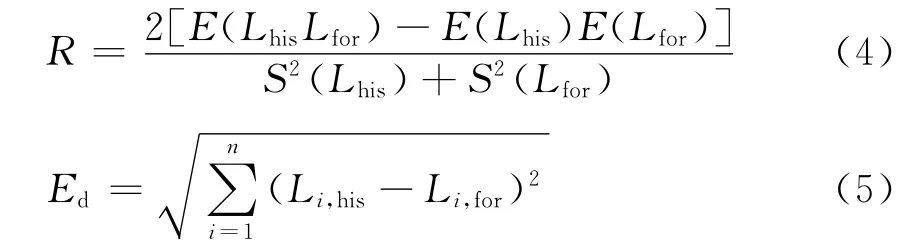
式（4）为曲线相似度计算公式，E为期望，S2为方差。－1≤R≤1，R反映了曲线的形态相似，而式（5）为欧氏距离公式，反映了曲线的空间距离。查找同时满足R趋近1而且Ed最小的若干日期作为相似日，由于需要求样本方差，所以相似日个数d≥5。

相似日的系统实际负荷与预测负荷之间仍然存在偏差，引入第φi点的偏移系数消除曲线之间的偏差为

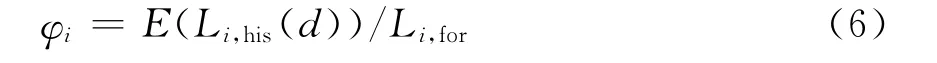
各相似日该点的各母线历史负荷Pi，his（m，d）组成二维数组。

2.2.2 母线预测值的修正范围

各母线历史负荷先除以偏移系数进行修正，再计算各母线负荷的期望和方差，方差越大的母线负荷在系统负荷相同时，其值波动范围越大，计算公式为

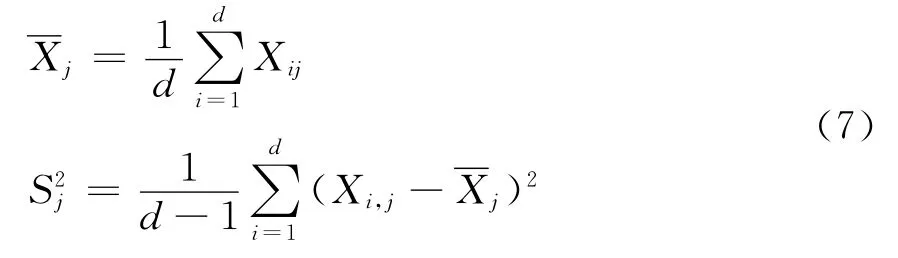
式中：Xij为各相似日母线j在时刻i的负荷组成的一维数组乘以偏移系数后φi的修正值，Xij＝Pi，j，his（d）／φi为样本期望；为样本方差。按正态分布分析该样本的规律，将该样本转变为标准正态分布的公式为

图3所示为标准正态分布的双侧α分位示意图，即图中阴影部分的面积所表示的概率值为α。若母线预测负荷Pij，for落在样本的双侧α分位点内则认为Pij，for准确不需要修改。取α＝0.1，查标准正态分布表得eα／2＝1.645，所以当Pij，for满足时，负荷90%的可能性分布在该区域内，不需要进行修正。

图3 标准正态分布的双侧α分位点Fig.3 Bilateralαsub－site of standard normal distribution

2.2.3 最优修正值的求解

要求母线j的预测值满足其式（9）所示的上下限约束，母线负荷预测之和也满足式（3）的约束，求最优修正解，采用最小二乘逼近，修正过程转变为求有约束问题的最优解。

图4所示为修正方法流程，该图中仅仅表示对某一个点的修正，针对修正过程建立二次规划问题，本文采用LINGO软件对二次规划问题求解，LINGO软件是美国LINDO系统公司开发的一款专门用来求解数学规划的软件，其功能十分强大，编程简单，是求解优化模型的最佳选择。

如果问题无解，则逐步减小k值，使母线总负荷有更大的调整范围，如果k达到最小值K时仍然没有解，则说明该点的系统负荷预测值可靠性不高，参照其进行母线负荷预测值进行修改无意义。

借鉴上文中母线负荷值调整范围的确定方法，同样假设系统负荷预测的准确率β服从正态分布，取负荷可靠率β为90%置信区间中的最小值，所以k的最小值K满足

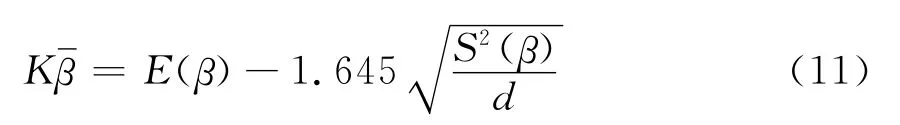
式中：E为期望；S2为方差。由于β＝E（β），即β的平均值等于期望，所以有

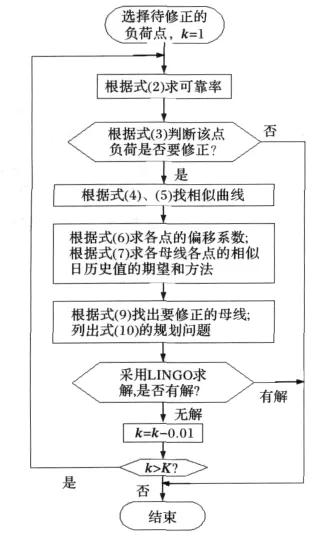
图4 修正方法流程Fig.4 Flow chart of revision method

3 算例验证

以图1所示的地区2010年7月23日为例，该年从6月开始进入高温天气，6月至7月23日系统负荷预测的平均准确率为95%，取k＝1，则δ＝0.95。对该日的第96点（23：45）负荷进行修正，该点的系统负荷预测值为888 MW，母线负荷预测值之和为820 MW。取89～96点的曲线计算曲线的相似度和欧氏距离查找相似曲线，取相似度R趋近1且欧氏距离最短的8条相似曲线对应的8个日期作为相似日。

求出得偏移系数为φ96＝0.9612，先求各母线负荷的期望和方差，再计算其上限和下限，共有10条母线需要进行负荷修正，如表1所示。利用LINGO软件求出修正后有最优解，计算结果如表1所示。

从表1可见，10条母线负荷中，有7条母线负荷为正修正，3条为负修正；有7条母线负荷修正后准确有所提高，3条修正后准确率有所降低。根据式（5）分别计算修正前后与实际值之间的欧氏距离，修正前为24.01，修正后为16.54。使用该方法对该日89～96点的负荷进行修正，修正后对母线负荷预测值的准确率进行统计如表2所示。从表中可以看出，参照系统负荷预测值对母线负荷进行修正后准确率得到升高的母线数目明显高于准确率下降的母线数目，所以该方法可行。

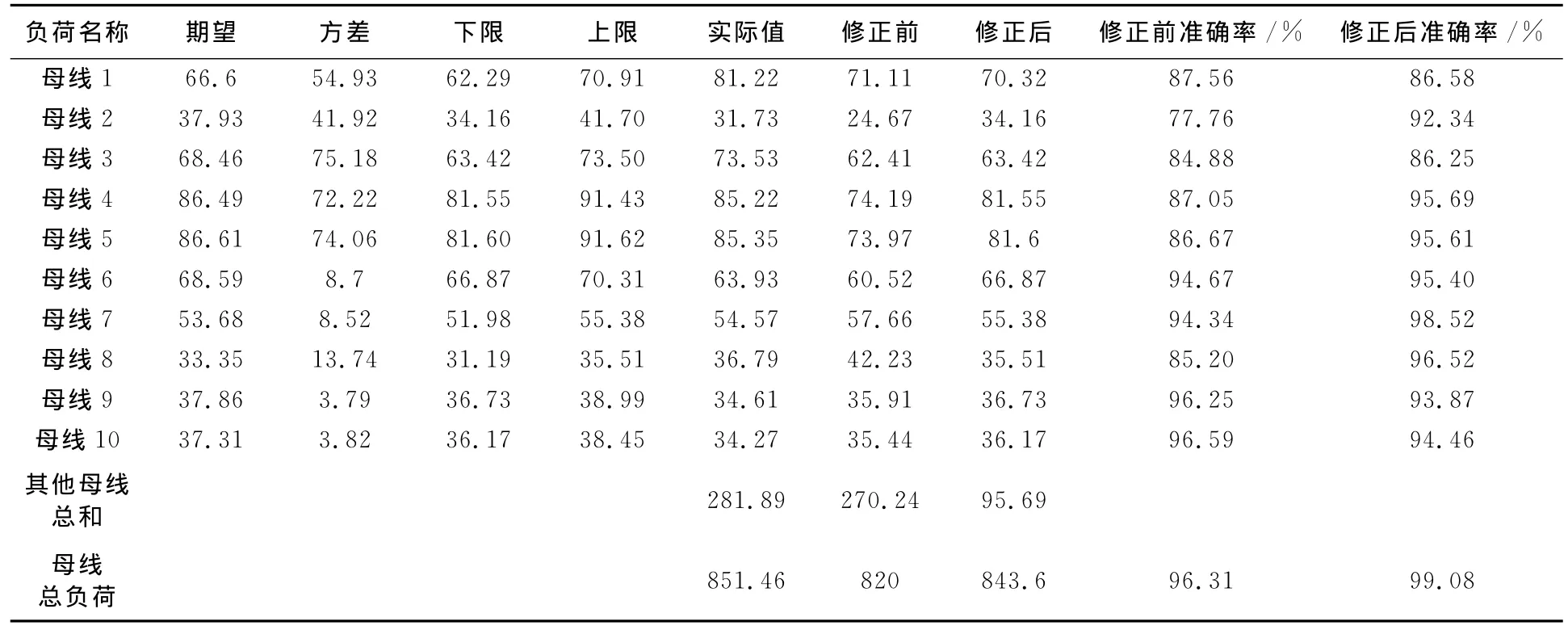
表1 母线负荷预测值修正前后对比Tab.1 Comparison of the bus load forecasting value before and after revision

表2 母线负荷修正后准确率变化趋势统计表Tab.2 Accuracy trend statics of bus load after revision

4 结语

对母线负荷进行分时间点修正，先分辨出需要修正的时间点，然后根据该点各母线相似日的历史数据的分布规律来决定其修正值的分布，采用最小二乘逼近，利用LINGO软件求最优解。实例证明修正后的母线负荷预测值整体上更加接近实际值，证明了该方法的可行性。

［1］ 于尔铿，刘广一，周京阳，等.能量管理系统［M］.北京：科学出版社，1998.

［2］ 康重庆，夏清，刘梅.电力系统负荷预测［M］.北京：中国电力出版社，2007.

［3］ 杨正瓴，田勇，张广涛，等（Yang Zhengling，Tian Yong，Zhang Guangtao，et al）.相似日短期负荷预测的非线性理论基础与改进（Nonlinear theoretical foundation and improvement of similar days method for short term load forecasting）［J］.电网技术（Power System Technology），2006，30（6）：63－66.

［4］ 李如琦，孙艳，孙志媛，等（Li Ruqi，Sun Yan，Sun Zhiyuan，et al）.基于PSRT与Elman神经网络的短期负荷多步预测（Short－term load multi－step forecasting based on PSRT and Elman neural network）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2007，19（6）：84－87，113.

［5］ 张红旭，姚建刚，曹伟，等（Zhang Hongxu，Yao Jiangang，Cao Wei，et al）.基于改进灰色模型的超短期负荷预测（Ultra－short term load forecasting based on improved gray model）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2009，21（6）：74－77.

［6］ 张振高，杨正瓴（Zhang Zhengao，Yang Zhengling）.短期负荷预测中的负荷求导法及天气因素的使用（Load derivation in short term forecasting using weather factor）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2006，18（5）：79－83.

［7］ 赵燃，康重庆，刘梅，等（Zhao Ran，Kang Chongqing，Liu Mei，et al）.面向节能发电调度的母线负荷预测平台（The platform of bus load forecasting for energy－conservation based generation dispatching）［J］.中国电力（Electric Power），2009，42（6）：32－36.

［8］ 魏少岩，吴俊勇（Wei Shaoyan，Wu Junyong）.基于灰色模型和Kalman平滑器的多母线短期负荷预测（Short－term bus load forecasting based on grey model and Kalman smoother）［J］.电工技术学报（Transactions of China Electrotechnical Society），2010，25（2）：158－162.

［9］ 王健（Wang Jian）.母线负荷预测系统的研究与实现（Study and Realization of Bus Load Forecasting System）［D］.长沙：湖南大学电气与信息工程学院（Changsha：College of Electrical and Information Engineering，Hunan University），2009.

［10］罗滇生，李伟伟，何洪英（Luo Diansheng，Li Weiwei，He Hongying）.基于局部形相似的超短期负荷预测方法（Very short－term load forecasting method on local shape similarity）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2008，20（1）：75－79.