线路保护中突变量检测的自适应算法

王鹏飞，余楚中，熊 伟

（1.重庆大学自动化学院，重庆 400030；2.重庆新世纪电气有限公司，重庆 400041）

继电保护的基本原理是利用被保护线路或设备故障前后某些突变的物理量为信息量，当突变量达到一定值时，起动逻辑控制环节，发出相应的跳闸脉冲或信号。基于突变量的继电保护由于具有原理简单，算法实现容易，灵敏度高，不受系统振荡、系统正常运行负荷以及非全相等因素的影响，在继电保护中得到了广泛的应用［1］。

突变量在微机保护特别是高压线路的保护中常被用作被保护对象是否发生故障的先行判据，一旦突变量元件动作则说明保护区内可能发生了故障，马上转入故障判别程序，若确诊为故障则出口跳闸或报警，此外突变量元件还广泛应用于操作电源闭锁、保护定值切换、振荡闭锁和故障选相等场合。因此，要求突变量启动判据必须具有极高的灵敏性，以免漏掉某些轻微故障而造成严重后果；同时在保证灵敏性的前提下尽可能减少误动［2］。

电力系统正常运行中存在着很多干扰，当故障发生时，对于突变量准确、快速地判断显得尤为重要。

1 突变量直接提取算法

1.1 一般算法

线路发生故障时，短路示意如图1所示（图中的虚线表示假设没有故障发生时的电流波形）。

当系统在正常运行时，负荷电流是稳定的，或者说负荷虽时时有变化，但不会在－个工频周期这样短的时间内突然变化很大，因此这时ik和ik－T应当接近相等。

如果在某一时刻发生短路，则故障电流突然增大，将出现突变量电流。其中，ik表示t＝k时刻的测量电流采样值；ik－T表示k时刻之前一周期，即t＝k－T时刻的测量电流采样值；Δik表示故障突变量的计算值；T为工频信号周期。

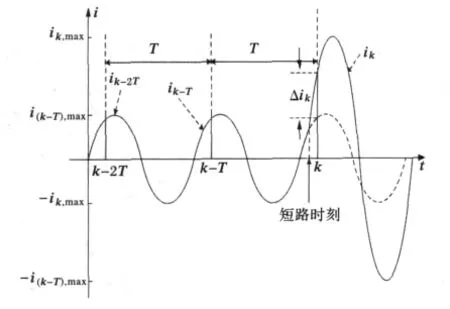
图1 故障前后的电流波形Fig.1 Current waveforms before and after fault

由此可以得到突变量电流的采样值计算公式为

根据式（1）可知，当系统正常运行时，Δik的值约等于0；当系统刚发生故障的一周内，Δik的值就是变量。这就是突变量电流的一般计算方法［3］。

式（1）的突变量计算法存在的一个问题是电网频率偏离50 Hz时，会产生一定的不平衡电流，因为ik和ik－T的采样时刻差20 ms，这决定于微机的定时器，它是由石英晶体振荡器控制的，十分精确和稳定，电网频率变化后，ik和ik－T对应电流波形的电角度将不再同相，而有一个差值Δθ，特别是当采样时刻落在电流过零附近时，由于电流变化较快，不大的Δθ将引起较大的不平衡电流。

1.2 改进后的算法

由于式（1）计算出的突变量电流容易受到电网频率波动影响，将式（1）改进得到式（2）来求取突变量电流。其原理是：如果由于频率偏离，造成ik和ik－T之间有一个相角差Δθ，则ik－T和ik－2T之间的相角差也应当基本相同，因而式（2）右侧两项可以得到部分抵消。特别是当计算的k时刻处在电流过零附近时，这两项各自都可能较大，但由于Δθ很小时，sinΔθ≈Δθ，所以这两项几乎完全抵消。用式（2）不仅可以补偿频率偏离产生的不平衡电流，还可以减弱由于系统静稳破坏而引起的不平衡电流［3］。

式（2）的应用中，对于故障的判断方法是：如果提取的突变量连续几点超过突变量电流定值，立即启动故障处理程序进行故障处理。但是当系统故障经过过渡电阻或者在远端故障时，可能不会出现连续几点突变的情况，这样启动元件只能采用稳态启动元件如零序电流启动元件、电流启动元件、静稳启动元件还有阻抗启动元件等。这些启动元件启动需要比较长的延时，不能快速进入故障处理［4］。

2 自适应面积算法

针对以上算法存在的不足，本文提出了一种新的突变量算法——自适应面积算法。基本原理是，取每个半周正弦波一段时间内电流积分绝对值（也即面积）的差值作为突变量电流的判断依据。当系统在正常运行时，由于负荷电流是稳定的所以求出的面积大小几乎是一样的，而当某个面积值较前个半周的面积值有较大变化，则说明系统发生了故障，有突变量电流产生。其算法原理如图2所示。

图2 自适应面积算法原理Fig.2 Schematic diagram of adaptive area algorithm

如图2所示（图中的虚线表示假设没有故障发生时的电流波形），SL，SL－1，…，SL－4分别表示第L个，L－1个到L－4个半周内阴影部分的面积；KL，KL－1，…，KL－4分别是第L个，L－1个到L－4个半周通过零点的时刻；iL（N／2－m）和iL（N／2＋m）表示第L个半周的第N／2－m和N／2＋m次测量电流采样值；ΔtL－1和ΔtL－2分别表示第L－1和L－2半周电流两次过零点的时间差；TS，L为第L个半周采样间隔；N为每个工频半周采样次数。

由于故障可能会发生在任何时候，所以图2中阴影部分的位置可以是各个半周波中任意相同的一块。本算法将阴影部分选择在故障发生概率较大的峰值处。具体应用中，以第N／2次采样值处作为中点，分别向前和向后各取m个采样值组成阴影部分。

根据图2可知，阴影部分的理论面积为

式中：I为电流有效值；α是积分起始点的初相角。

在实际应用中，利用梯形法则可近似求出

为了克服电网频率变化的影响，在式（4）中采用采样频率跟踪的自适应算法，即TS，L的值根据电网频率的变化而变化。规定每个半周等间隔采样N次不变，利用定时器实时的测量电流波形的过零点，求出每个半周的两个过零点处的时间差Δt并将此作为下个半周采样间隔大小的依据。每个工频半周调整一次采样频率。如图2所示，即可求出

由图2可以看出每个阴影部分包括N／2＋m减去N／2－m共2m个采样值。其中m的值根据系统正常运行时电流的幅值大小来确定。

一个周期内，幅值越大，电流波形就越陡峭，当突变量发生时面积的变化较小；反之，幅值越小，电流波形就越平缓，因而突变量发生时面积的变化就较为明显。

所以，为了准确、快速的判断突变量，当电流幅值较小时，相应的m的取值也较小，电流幅值较大时，相应的m的取值也要变大。

假设测得电流的幅值为Ia，可测量的电流幅值的最大值是Imax。一般按照以下公式选取m的值。

以上是SL的计算方法，其他阴影部分的面积求法与此类同；求出面积后，突变量计算式为

当ΔS＞Sft时，认为突变量发生。Sft为判断突变量是否发生的浮动门槛值，其取值大小可调整。一般取Sft＝（0～1／2）SL。

以上算法假设时故障电流是标准的正弦波，实际中，故障电流一般含有高频等非周期分量。不过这些非周期分量的存在对于SL的计算值不会有太大影响，故此自适应算法在这些情况下同样适用。

3 动模仿真实验

基于本文提出的自适应算法检测突变量，设计出220 k V线路微机保护装置，在国家继电器质量监督检验中心的动模试验中得到了验证。实验过程及结论如下。

仿真模型原理接线如图3所示，为单机对无穷大系统，双回无互感线路，保护装设在L 1线路两侧。模型系统参数如表1所示。

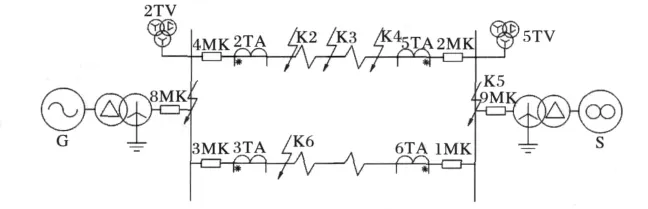
图3 仿真模型示意Fig.3 Schematic diagram of simulation model

表1 模型系统参数Tab.1 System parameters of model

本次实验，利用动模实验室的DF1024波形分析系统对以上线路进行故障录波，该装置可以设置启动判据对电力系统及设备异常运行状况和故障进行自动录波。试验中本算法有关参数取值为：采样次数N＝24，Imax＝5 A，浮动门槛Sft＝SL／3。取K2点A相接地短路时的故障波形，如图4所示。

从图中可看到，当A相短路时，A相电流NIa急剧变大，在故障发生13.20 ms时，突变量启动元件TN动作。完全满足快速保护的要求。

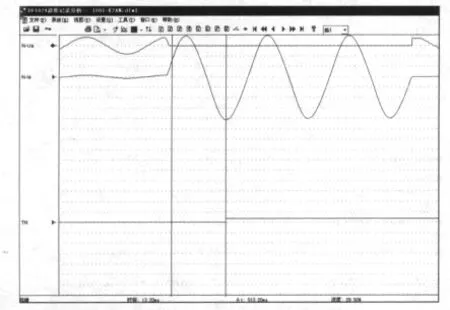
图4 故障电流波形Fig.4 Fault current waveforms

4 结语

本文提出的自适应面积突变量检测算法弥补了现有算法存在的不足，用积分方式计算突变量取代了以往直接提取突变量的方法，采样间隔和面积宽度可以自适应调整。通过动模实验验证了此算法是可行的，并且具有反应速度快，准确性高，抗干扰能力强等优点。

［1］ 陈卫，尹项根，陈德树，等（Chen Wei，Yin Xianggen，Chen Deshu，et al）.基于补偿电压的突变量方向判别原理（The ultra high－speed directional protective relaying based on fault component of compensation voltage）［J］.电力系统自动化（Automation of Electric Power Systems），2002，26（14）：49－51，66.

［2］ 李佑光，林东.电力系统继电保护原理及新技术［M］.北京：科学出版社，2009.

［3］ 杨奇逊，黄少锋.微型机继电保护基础［M］.北京：中国电力出版社，2007.

［4］ 刘剑飞，刘丰艺（Liu Jianfei，Liu Fengyi）.突变量启动元件在微机距离保护中的应用（The break－variable starting element application in digital distance protection）［J］.电力建设（Electric Power Construction），2009，30（5）：94－96.

［5］ 陈志亮，范春菊（Chen Zhiliang，Fan Chunju）.基于5

次谐波突变量的小电流接地系统选线（Fault line selection for small current neutral grounding system based on the fifth harmonic current mutation in distribution system）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2006，18（5）：37－41，69.