三轴机床微细异型电极加工与尺寸误差分析

郭学杰,裴万生,余祖元,李剑中

(大连理工大学机械工程学院,辽宁大连116024)

与传统机械相比,微机械体积小、耗能低、性能稳定,在航空航天、医学、生化、通讯等领域具有广泛需求。而微细电火花加工作为微细加工技术的一种,因其可加工任何导电材料而无需考虑材料的硬度,而被广泛应用于微孔和微型磨具的加工。日本学者发明了线电极磨削技术[1],解决了微细工具电极的在线制作问题,推动了微细电火花技术的应用,同时促进了对微细电火花加工技术的深入研究。余祖元等通过复合电极摇动和工件超声振动的方法加工出了深径比达29的微孔[2]。

本文利用三轴微细电火花加工机床,通过直线插补与圆弧插补方法,分别加工出了圆锥台、四棱台以及带有圆弧曲面的微细异型电极,并获得了较高的加工尺寸精度。

1 插补算法

1.1 直线插补原理

数控加工中,按脉冲驱动方式的不同有脉冲增量插补和数字增量插补。脉冲增量插补主要用于步进电机驱动的开环系统;数字增量插补主要用于采用交、直流伺服电机为伺服驱动系统的闭环、半闭环数控系统,也可用于以步进电机为伺服驱动系统的开环数控系统。本文所用实验机床为双闭环直流伺服系统,因而选用了数据采样插补法。

直线插补的基本原理如图1所示,假设要加工的直线OP在XY平面上,起点坐标为坐标原点O(0,0),终点坐标P为(x0,y0),刀具进给方向和X轴夹角为θ。设插补进给步长为 Δ L,则插补步数N为:

数控加工中,插补步数应是整数,即应对上式的结果取整。插补过程中,前(N-1)步所走步长均为Δ L,第N步走完剩余长度。通过取速度的正弦值和余弦值来保证X、Y轴同时到达终点。

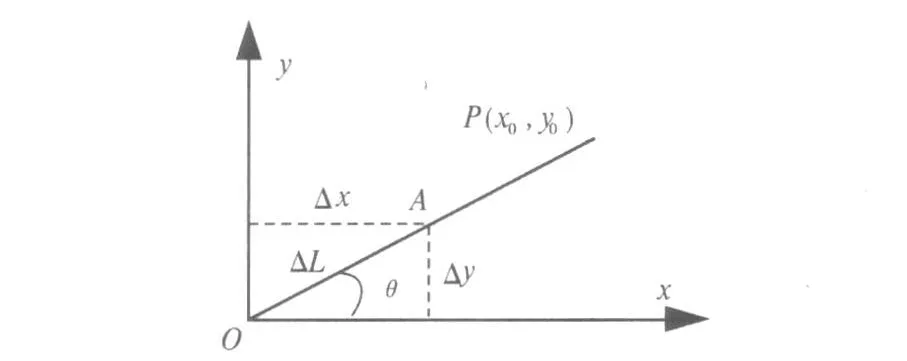
图1 直线插补原理

1.2 圆弧插补原理

圆弧插补的基本原理如图2所示,设圆弧起点与终点为 A(x0,y0),B(xe,ye)。P(xi,yi),Q(xi+1,yi+1)为相邻两个插补点。根据圆的参数方程有:

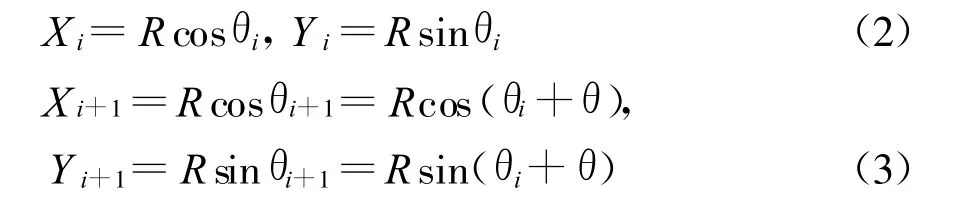
式中:R为圆弧半径,θ为步长 Δ L所对应的步距角。

由P、Q两点的坐标可计算出弦PQ与X轴的夹角,进而计算出每步X轴、Y轴的速度。设插补进给步长为 Δ L,则加工圆弧AB的插补步数N为:

同直线插补一样,插补步数须为正整数,即前(N-1)步每步所走角度为步距角 θ,第 N步走完剩余角度。

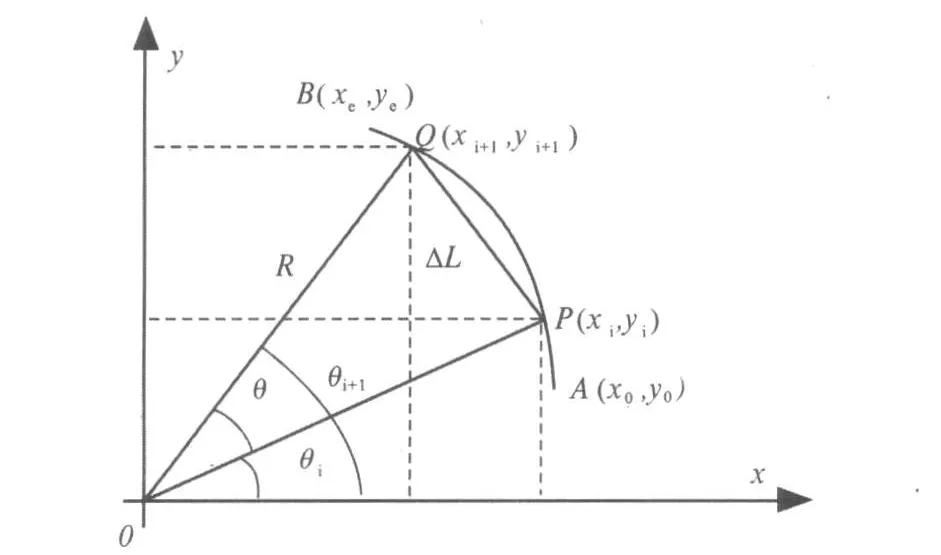
图2 圆弧插补原理

1.3 基于labview的插补算法

根据以上直线插补与圆弧插补原理,本文使用labview编制的插补算法(图3)。

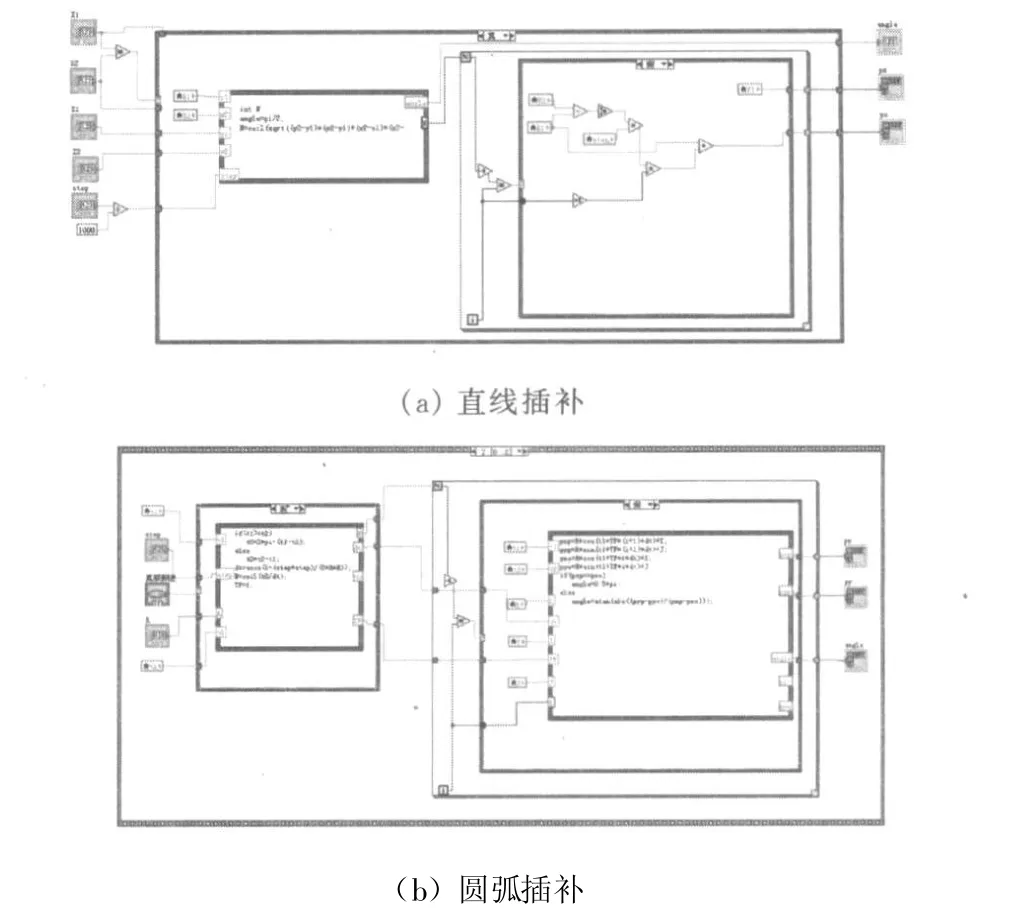
图3 基于labview的插补算法

2 微细异型电极加工

2.1 微细异型电极加工原理

微细电极的制备采用线电极电火花磨削(WEDG)方法。如图4所示,线电极在导向轮上连续低速移动,工件(待成形的工具电极)则根据需要随机床主轴旋转和进行三维运动。若通过所设计的插补算法,实现主轴在XZ平面走斜线与圆弧轨迹,并配合主轴的旋转与否,则可在三轴卧式微细电火花机床上加工出圆锥、棱台等各种形状复杂的微细异型电极。

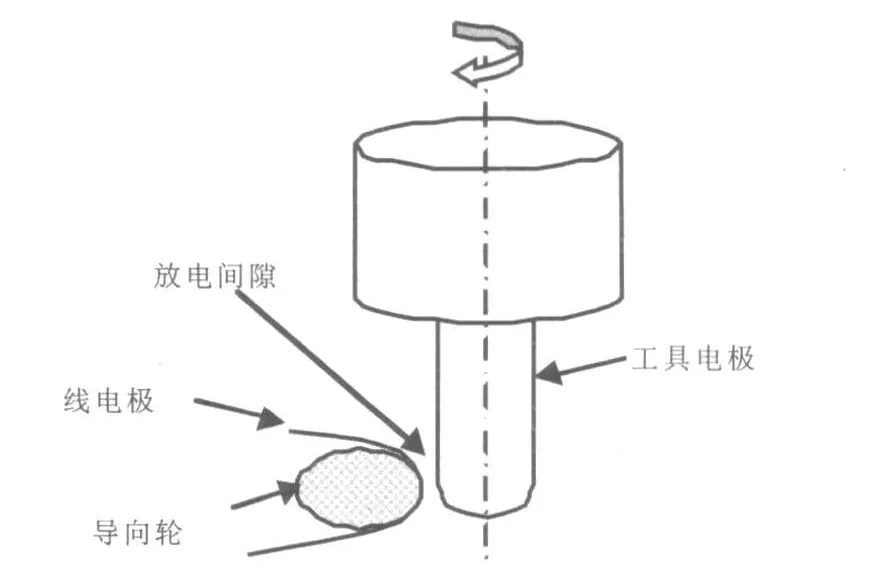
图4 WEDG加工原理图

2.2 微细异型电极的加工结果

图5为预加工微细异型电极的设计尺寸,表1为其加工参数,图6为其在卧式微细电火花机床上的实际加工结果照片。

表1 微细异型电极加工参数

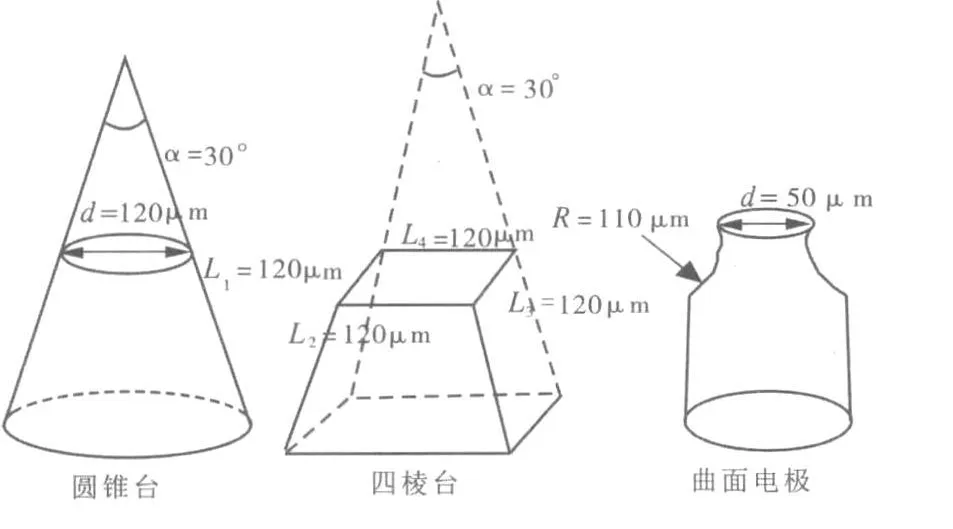
图5 微细异型电极的设计尺寸

图6 加工的微细异型电极

2.3 微细异型电极尺寸误差

加工后微细异型电极的尺寸测量在SMS&OLYSIM测量显微镜上进行。设计尺寸、测量结果及尺寸误差如见2～表4。由表2～表4可知,微细异型电极加工后的尺寸相对误差均在2%以内,说明插补算法有较高的精度。

表2 圆锥台尺寸误差

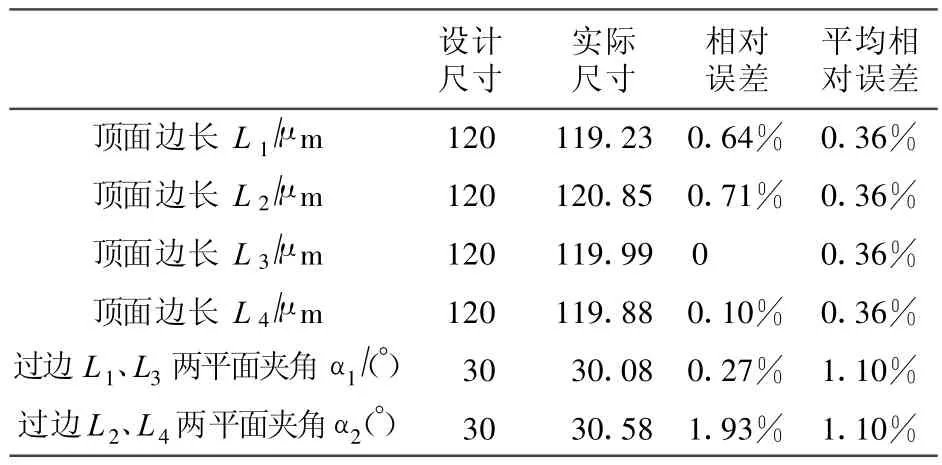
表3 四棱台尺寸误差

表4 曲面电极尺寸误差

2.4 尺寸误差原因分析

(1)放电间隙

为研究加工条件下放电间隙的变化,预先进行了10组微孔的加工,表5为通过测量孔径与电极直径后计算出的放电间隙。由表5可见,同样条件下加工获得的微孔,其放电间隙在11.2～18.3 μm的范围变化,说明放电间隙具有随机性,因而导致异型电极加工的尺寸误差。

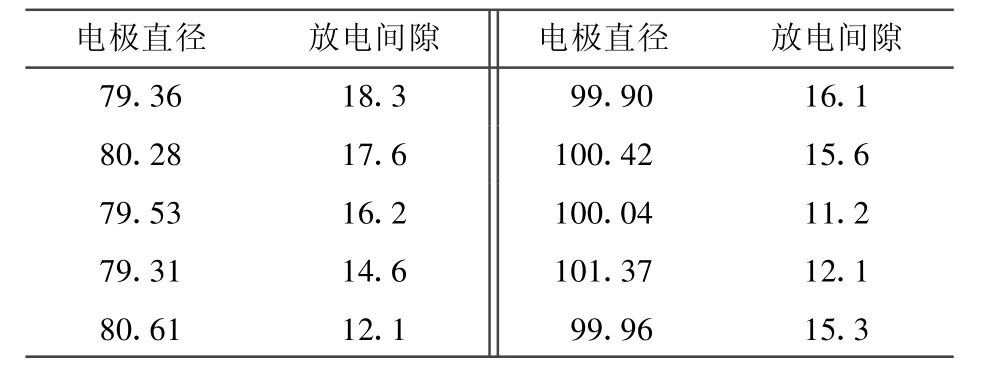
表5 钻孔实验的放电间隙 μm

(2)机床精度

插补的思想是用微小折线来逼近所要加工的线形,进给步长 Δ L越小则插补点越多,插补曲线就越接近所要加工的线形,加工精度也就越高;但 Δ L的取值也要考虑到机床运动平台的最小分辨率。实验加工设备采用德国 Physik Instrumente公司的M-521型高精度运动平台,其最小分辨率为0.1 μm。因而实验中 Δ L的值取为0.3 μm,这是导致异型电极加工误差的另一原因。提高机床运动平台的精度,减小进给步长,能减小电极尺寸误差。

(3)测量误差

测量采用的SMS&OLYSIM测量显微镜,其测量误差为±1 μm。也是导致异型电极加工误差的原因之一。多次测量求平均值,可减小电极尺寸误差。

3 总结

采用直线插补与圆弧插补算法,在三轴微细电火花机床上实际加工出了圆锥台、四棱台以及带有曲面的微细异型电极,并对微细异型电极尺寸误差进行计算,其相对误差均在2%以内,说明插补算法有较高的精度。本文最后对微细异型电极尺寸误差的形成原因作了全面分析,分析得到放电间隙的随机性、机床运动精度、尺寸测量精度等均是导致误差形成的原因。

[1] Masuzawa T,Fujino M,Kobayashi K,et al.Wire electro-discharge grinding for micro-machining[J].Annals of the CIRP,1985,34(1):213-216.

[2] Yu Zuyuan,Zhang Y,Li J,et al.High aspect ratio micro-hole drilling aided with ultrasonic vibration and planetary movement of electrode by micro-EDM[J].Annals of the CIRP,2009,58:213-216.