双轴对称不锈钢受弯构件变形性能的非线性分析＊

王元清 高 博 戴国欣 石永久

（清华大学土木工程系土木工程安全与耐久教育部重点实验室1） 北京 100084）

（中国建筑西南设计研究院有限公司2） 成都 610081） （重庆大学土木工程学院3） 重庆 400045）

0 引 言

不锈钢因其良好的耐腐蚀性、耐久性以及美观大方等优点，在建筑结构中得到了越来越广泛的应用［1］.与普通碳素钢相比，不锈钢材料的应力－应变关系是一条连续光滑的曲线，没有明显的屈服点和屈服平台［2］，见图1.

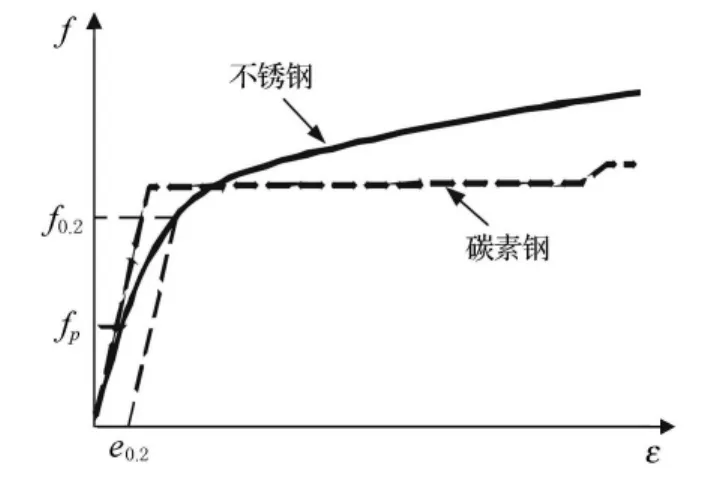
图1 不锈钢与碳素钢应力－应变关系的比较

其本构关系可以用Ramberg－Osgood方程描述［3］：

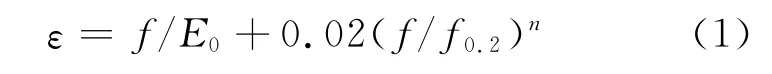
式中：n为应变强化系数，也称材料系数，n＝ln 20／ln（f0.2／f0.01）；f0.2和f0.01分别是残余应变为0.2%和0.01%时所对应的应力.通常把f0.2作为其强度标准值.

由于不锈钢具有明显的材料非线性，使得其受弯构件的荷载－挠度曲线也会表现出非线性，荷载越大，变形的非线性就越强.目前，欧洲规范［4］、澳大利亚和新西兰规范［5］、美国规范［6］在不锈钢受弯构件的荷载－挠度计算方面均采用线性的方法，引入割线模量来考虑不锈钢材料非线性的影响，计算结果具有一定偏差［7］.本文的研究目的就是给出双轴对称的不锈钢受弯构件荷载－挠度关系较为准确、简洁的计算方法.

1 有限元建模

不锈钢材料在受拉和受压过程中其应力－应变性能表现出明显的各向异性和非对称性［8］，为简化分析，有限元模型不考虑不锈钢材料的各向异性，研究表明这种简化带来的误差可以接受［9］.

图2为有限元模型的网格划分情况.本文计算了两端简支和两端固支的双轴对称工字梁，考虑承受跨中集中荷载和满跨均布荷载2种情况进行参数化分析.梁的侧向位移被约束，避免整体失稳.

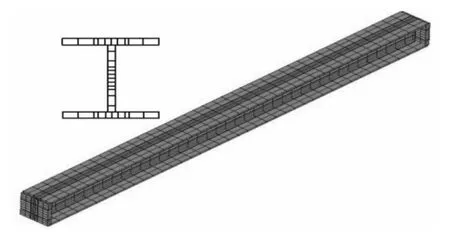
图2 有限元模型及网格划分

根据GB 4237－200710选择5种牌号的不锈钢材料，其应力－应变关系按式（1）计算，其中材料系数n通过材料应力－应变曲线反算得出，如表1所列.

由于目前国内厂家尚无法生产不锈钢型钢，因此不锈钢截面采用焊接，需要考虑焊接残余应力的影响.焊接工字形截面的残余应力分布参考Gardner等［11］建议的模型，如图3所示.

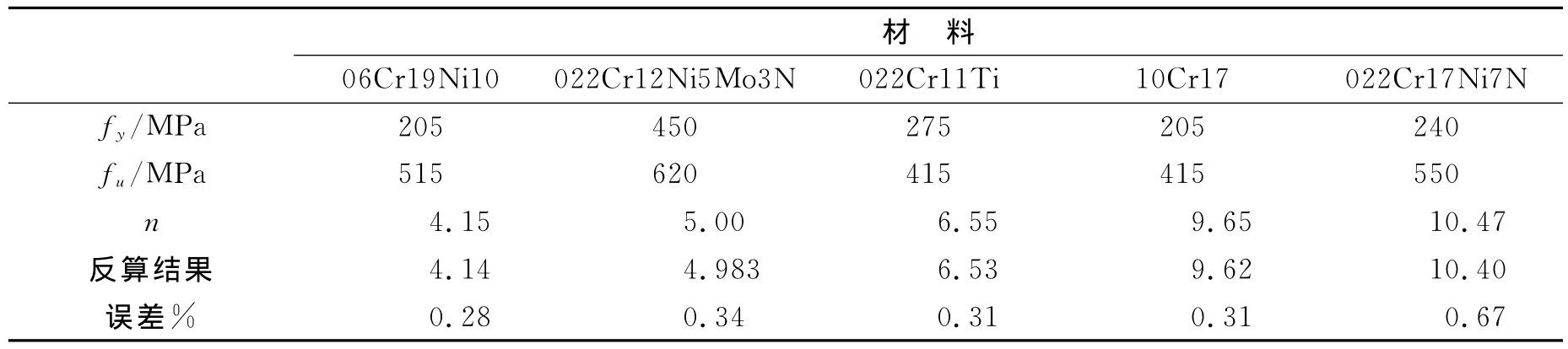
表1 不同牌号不锈钢的材料系数

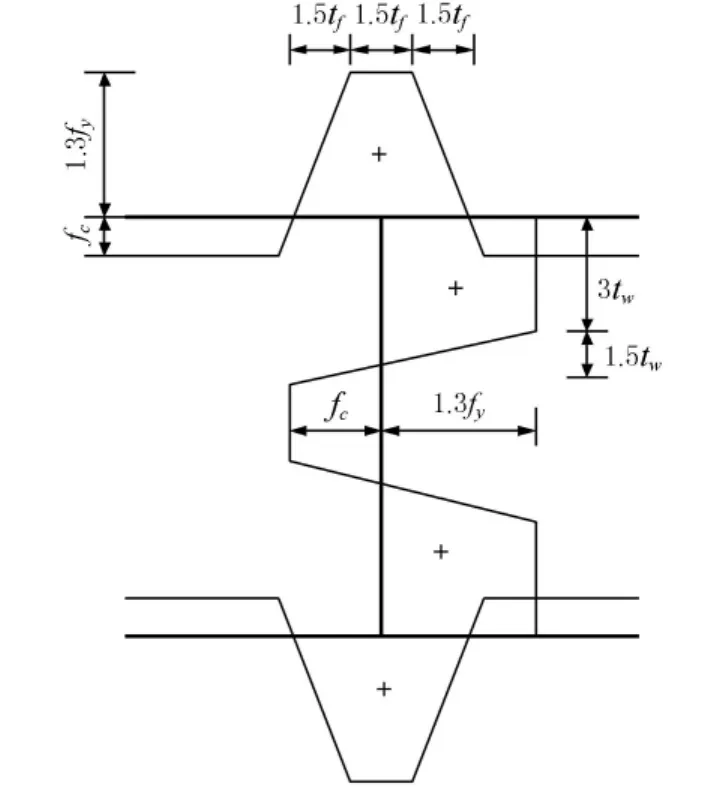
图3 不锈钢焊接工字形截面残余应力模型

有限元分析中实际采用的残余应力分布简化模型如图4所示，其中正值表示残余拉应力，负值表示残余压应力.计算中考虑板件的初始不平直度为板宽的1／500［12］，初始缺陷的形式参考一阶屈曲模态，计算中开启二阶效应，应用弧长法.

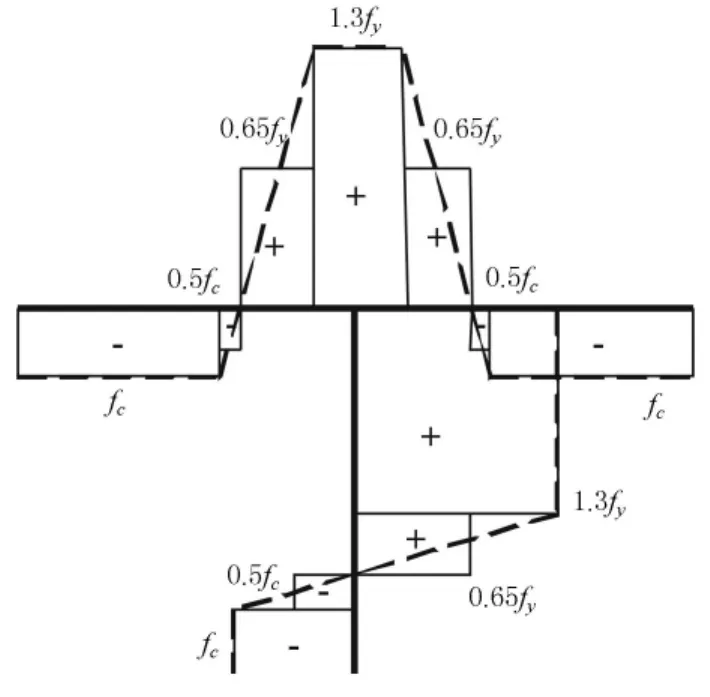
图4 有限元分析采用的残余应力简化模型

2 影响因素分析

本文主要分析了材料系数、截面形状系数、构件长细比以及荷载作用形式等因素对两端简支的不锈钢梁w／w0.2与 M／M0.2关系的影响.其中，M为受弯构件跨中截面的实际弯矩；M0.2＝Wfy是截面的弹性极限弯矩，W 为初始弹性截面模量；w是受弯构件跨中的真实挠度；w0.2是假设材料为线弹性时，与M0.2对应的跨中挠度.

1）材料系数的影响 由图5a）可以看出，材料系数n对构件的荷载－挠度关系影响较为显著.n值越小，材料的非线性越强，其荷载－挠度关系的非线性也越强.

2）截面形状系数的影响 截面形状系数是指全塑性截面模量与弹性截面模量之比，即α＝Z／W.图5b）表明，截面形状系数对荷载－挠度关系的影响较为显著.

3）构件长细比的影响 本文所指的长细比是指截面对强轴的长细比，由图5c）可以看出，在构件发生整体失稳前，其荷载－挠度曲线基本是一致的，长细比对荷载－挠度关系的影响非常小，因此本文在后续分析中将构件侧向可靠约束，避免发生整体失稳.

4）板件宽厚比的影响 图5d）可以看出，板件宽厚比对构件承载能力影响非常大，过早的发生局部屈曲会严重降低构件承载能力.但是在发生局部失稳前，板件宽厚比对荷载－挠度关系的影响非常小，因此在后面的有限元分析中将构件的板件取得较厚，避免发生局部屈曲.

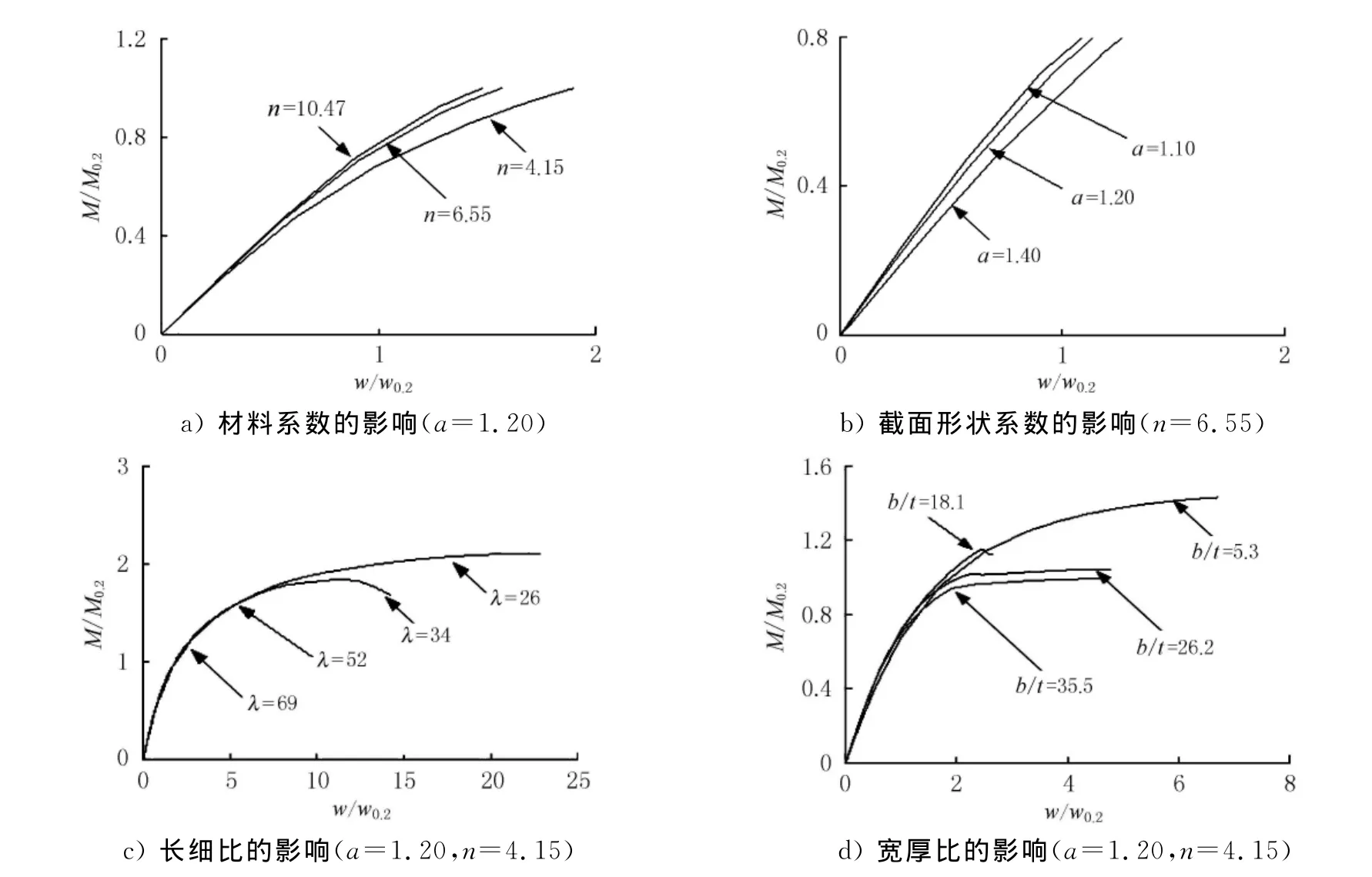
图5 不锈钢受弯构件荷载－挠度曲线的影响因素

5）构件截面形式的影响 由图6a）可知，由于箱形截面腹板对翼缘的约束作用较强，对于初始缺陷的敏感程度较小，有限元计算得到的跨中挠度比相同条件下的工字形截面梁要小.

图6 截面形式和荷载作用形式对构件变形的影响

6）荷载作用形式及边界约束条件的影响图6b）显示了两端简支工字梁在均布荷载和跨中集中荷载作用下的荷载－挠度曲线.在构件截面形式和跨中弯矩相同的情况下，与集中荷载作用时相比，均布荷载作用下构件的弯矩图更加饱满，当跨中截面进入塑性状态后，其两侧较大范围内的梁段也会达到塑性阶段，于是产生较大的塑性挠度，其荷载－挠度曲线的非线性也就越强；此外，本文还分析了两端固支以及一端固支一端简支的情况，通过分析可知，此时可以忽略梁的塑性挠度，引入割线模量，按照线性方法进行计算.

由上述的分析可知，不锈钢的材料系数n以及截面形状系数α对受弯构件的荷载－挠度关系影响较为显著；箱形截面可以按照与工字形截面相同的方法求解，得到的结果会偏于保守.对于双轴对称工字形截面α＝1.1～1.2，加强上翼缘或下翼缘的截面α＝1.2～1.4.因此，考虑α＝1.1～1.4；n＝4.15～10.47的参数组合进行参数化有限元分析，分别计算了均布荷载和跨中集中荷载作用下两端简支和两端固支不锈钢工字梁共180根荷载－挠度曲线，用于后面公式的非线性拟合.

3 一种计算不锈钢受弯构件非线性变形的新方法

3.1 新方法的提出

目前国外规范计算不锈钢受弯构件的非线性变形是基于材料力学中的线弹性方法，引入割线模量来考虑不锈钢材料的非线性［13］.Real［14］则基于不锈钢受弯构件的弯矩－曲率关系，提出了一种新的方法，如式（2）.

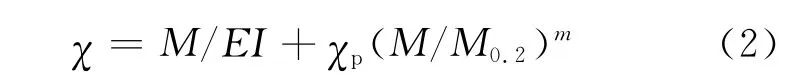
式中：χ为截面曲率；χp为对应于 M0.2的塑性曲率；m为系数.现将式（2）进行简单的变形，如式（3）所示.

式中：χ0.2为对应于 M0.2的截面曲率；b，c为系数，与前面所分析的参数有关.本文参考石永久［15］等人对铝合金梁变形性能的处理方法，将式（3）沿着梁长方向积分两次，得到构件荷载－挠度的关系式：

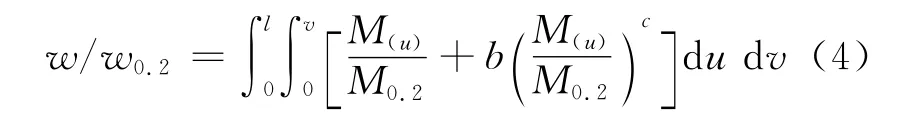
式（4）的积分结果可以进一步简化为

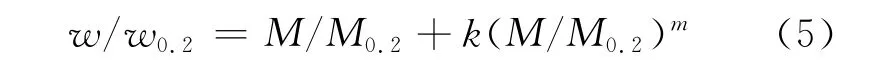
式中：k，m为系数，也与前面所分析的参数有关.其具体数值可以利用有限元计算结果进行非线性拟合得到.

3.2 公式拟合

通过对有限元结果的分析发现按式（5）拟合的结果误差较大，因此引入修正系数p，按式（6）对结果进行非线性拟合.

式中：系数k，m，p与材料系数n、截面形状系数α有关，且它们之间呈现明显的非线性关系.通过分析，采用式（7）拟合各系数的值.

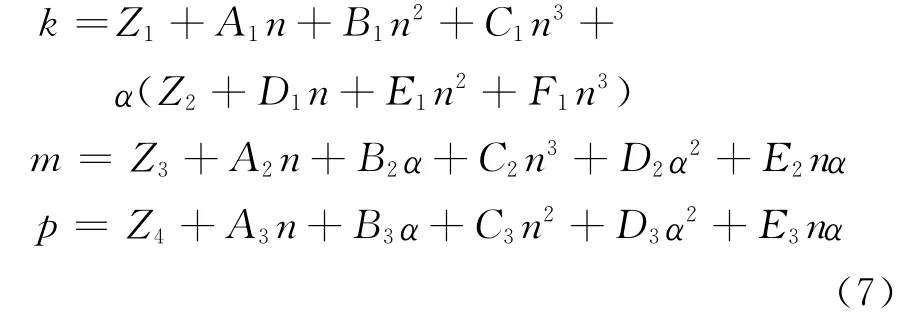
式中：Zi，Ai，Bi，Ci，Di，Ei，Fi是待定系数.

3.3 拟合结果

1）两端简支工字梁在跨中集中荷载作用下：

2）两端简支工字梁在满跨均布荷载作用下：

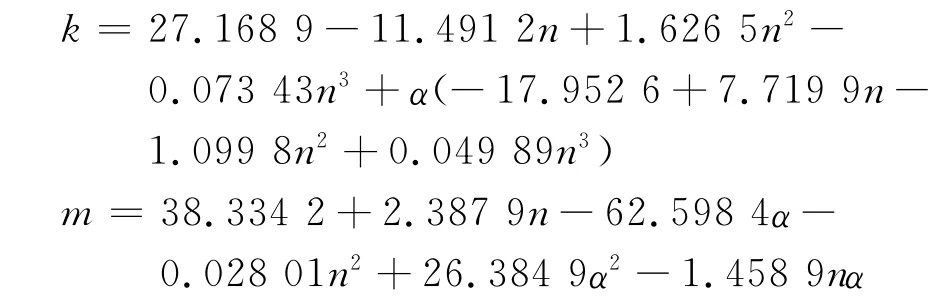
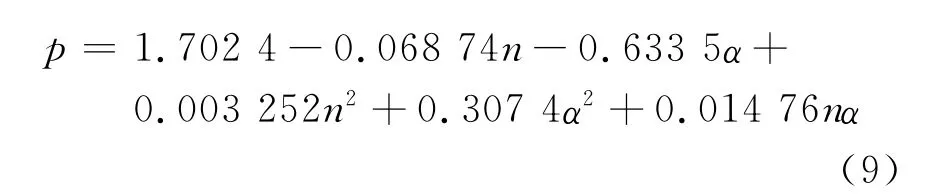
用式（6）、（8）或（9）计算双轴对称不锈钢受弯构件的荷载－挠度曲线，大部分计算结果与有限元结果吻合良好（如图6），误差可以控制在5%以内，只有小部分计算结果在M／M0.2＞0.9时误差较大，见图7.

图7 公式计算结果和有限元结果的比较

4 结 论

1）不锈钢材料应力－应变关系具有明显非线性，其受弯构件的荷载－挠度曲线应按照非线性的方法求解.

2）不锈钢受弯构件的荷载－挠度关系与材料系数、构件的截面形状系数、构件的截面类型以及荷载分布类型有关.本文基于有限元方法进行了参数化分析，经非线性拟合给出了双轴对称不锈钢工字梁的荷载－挠度关系计算公式，其计算结果与有限元结果吻合较好.

3）对于两端固支以及一端固支一端简支的不锈钢工字梁，可以忽略梁的塑性变形，按照线性的方法进行求解其荷载－挠度曲线.箱形截面梁也可以采用与工字形截面梁相同的公式进行计算，计算结果略偏保守.

此外，本文在有限元分析中并没有考虑整体失稳和局部失稳对构件变形性能的影响.由于本文分析所采用的截面均为焊接组合截面，组成板件均具有相当厚度，不会发生畸变屈曲，且截面关于受弯轴是对称的，因此也没有考虑构件的扭转和翘曲.

［1］BEN Young.Experimental and numerical investigation of high strength stainless steel structures［J］.Journal of Constructional Steel Research，2008，64（11）：1225－1230.

［2］王元清，高 博，戴国欣，等.不锈钢受弯构件承载性能的研究进展［J］.建筑结构学报，2010，31（S1）：189－194.

［3］王元清，袁焕鑫，石永久，等.不锈钢结构及其应用和研究现状［J］.钢结构，2010，25（2）：1－13.

［4］EN 1993－1－4.Eurocode 3：design of steel structures－Part 1－4：general rules－supplementary rules for stainless steels［S］.2006.

［5］AS／NZS 4673：2001.Cold formed stainless steel structures［S］.2001.

［6］ASCE.Specification for the design of cold－formed stainless steel structural members［S］.2002.

［7］高 博，王元清，戴国欣，等.各国规范不锈钢受弯构件设计方法比较分析［J］.四川建筑科学研究.2010，36（5）：1－4.

［8］GARDNER L.The use of stainless steel in structures［J］.Progress in Structural Engineering and Materials，2005，131（7）：45－55.

［9］RASMUSSEN K J R，BURNS T，BEZKOROVAINY P，et al.Numerical modeling of stainless steel plates in compression［J］.Journal of Constructional Steel Research，2003，59：1345－1362.

［10］中华人民共和国国家标准.GB／T 4237－2007不锈钢热轧钢板和钢带［S］.北京：中国标准出版社，2007.

［11］GARDNER L，CRUISE R B.Modeling of residual stresses in structural stainless steel sections［J］.Journal of Structural Engineering，2009，135（1）：42－53.

［12］GULVANESSIAN H，CALGARO J A，HOLICKY M.Designers′guide to EN 1990eurocode：basis of structural design［M］.London：Thomas Telford Ltd.，2002.

［13］BADDOO N R .A comparison of structural stainless steel design standards［C］／／Proceedings of the Stainless Steel Structures International Experts′Seminar.Ascot，UK，2003：131－150.

［14］REAL E，MIRAMBELL E.Flexural behavior of stainless steel beams［J］.Engineering Structures，2005，27：1465－1475.

［15］石永久，程 明，王元清.铝合金受弯构件变形性能的非线性分析［J］.四川大学学报：工程科学版，2006，38（1）：10－14.