集装箱港口岸边资源泊位与岸桥协同优化配置研究*
王正君 韩晓龙
(上海海事大学物流研究中心 上海 200135)
0 引 言
集装箱港口作为物流系统的一个重要节点,是联接海陆运输的一个枢纽.随着经济的发展,集装箱船舶不断向大型化发展,同时港口的吞吐量也逐年递增.而集装箱港口建设投资巨大,一旦建成,很难对其进行改建.作为一个集装箱港口,提高竞争力最有效的方式,就是提高对集装箱运输船舶的作业效率,在减少港口作业的成本的同时提高船公司对港口服务的满意度.整个集装箱港口的物流操作可以分为3部分:(1)岸边操作;(2)场内操作;(3)连接岸边与堆场的水平运输.一个集装箱港口的物流过程见图1.
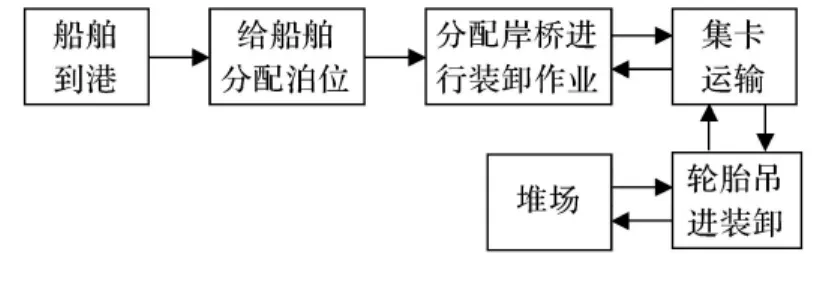
图1 港口物流流程图
20世纪90年代以来,产生了大量有关集装箱港口的优化模型.本文研究了在连续泊位条件下,泊位与岸桥2种资源的协同优化配置问题.本文的特点在于考虑了2个非常实际的问题:岸桥的工作范围;岸桥在装卸工作时在一定范围内进行调整.这些约束的加入使模型更接近实际情况.最后建立了一个混合整数规划模型,并采用两阶段分解方法进行求解.第一阶段不考虑岸桥的覆盖范围条件下,为船舶分配泊位与岸桥.然后第二阶段再根据岸桥的覆盖范围对第一阶段的岸桥分配进行调整,产生最终的岸桥工作时间表.
岸桥在装卸过程中调整的意思是,在装卸过程中,分配给船舶的岸桥数目的变化,或者是具体的某个岸桥作业的变化.在很多文章中是不考虑装卸过程中岸桥的调整的.然而,在这种情况下岸桥的利用是比较低的,因为空闲的岸桥不能及时移动到需要它们的地方.还有一种情况是在装卸过程中岸桥可以随意的移动.这会导致太多的岸桥开始时间,同样也会导致岸桥工作效率的低下.因此,从一个实际的角度出发,在一定范围内限制岸桥在装卸作业中的调整更好.在本文中规定岸桥在工作中最多调整一次.
1 文献综述
集装箱港口岸边操作问题中主要涉及的资源为泊位资源和岸桥资源,目前国内外学者已进行了一些研究,针对泊位和岸桥的研究大多数都将他们分开来处理.泊位分配一般是确定船舶在泊时间和在港口位置.刘志雄[1]针对离散泊位问题,以最小化所有船舶在港时间最短为目标,在不考虑岸桥资源的影响下,建立了港口泊位调度问题的数学模型,并用粒子群算法对泊位调度问题进行优化.秦进[2]提出了一个新的离散泊位分配模型,对船舶在港口的服务时间以及港口泊位的可用时间,都考虑了时间窗约束.在目标函数中,还考虑到船舶的不同服务时间价值.然后用模拟退火算法对问题进行了计算与分析.此外相关的研究 还 有 Kim 和 Moon[3],Imai[4],Monaco 和Sammarra[5]等.
岸桥分配一般处理分配给一艘船的岸桥在船舶贝位上的工作序列.相关的研究有:Lim[6]对于集装箱船舶没有相互影响的条件下静态的桥吊调度问题进行了研究,他们把到来的集装箱船舶作为一个作业,桥吊分配给船舶作业完成之后都有一个收益,他们的目标函数是使总的收益最大化.Lee Derhorng[7]研究了桥吊之间有相互影响的桥吊分配问题,对于桥吊分配模型,作者提出了一个混合整数规划模型,因为这是一个NP-hard问题,作者提出了利用遗传算法对问题进行求解,计算结果显示遗传算法能够有效的解决桥吊的分配问题.
一艘船在港口的停靠时间直接取决于这艘船所分配的岸桥数量.分配的岸桥数越多,船舶的周转时间一般也就越快.但将泊位分派和岸桥分开来研究得到的结果很可能是资源使用的局部最优,而得不到全局最优.先前的研究,大多是将泊位资源与岸桥资源分开来研究的,对于将两种资源协同优化的研究比较少.相关方面的研究有:Han Xiaole[8]研究了泊位和桥吊的协同调度问题.研究了在不确定船舶的达到时刻和集装箱的作业时间、泊位是离散条件下,具有不同优先级的船舶动态到达,桥吊允许在作业完当前船舶之后移动到其他的泊位对其他船舶进行作业.作者提出了一个混合整数规划模型,并用遗传算法进行了求解.泊位被看做是离散的情况下,泊位的利用相对来说比较低,尤其是船舶的长度远远小于泊位的长度的时候.韩晓龙[9]研究了连续泊位下的泊位-桥吊分配问题,建立了泊位-桥吊配置模型,用启发式回溯算法对模型求解,并用VB+Access开发了泊位配置辅助系统(BAAS).Park和Kim[10]将泊位看做是连续的,并提供了一个两阶段的解决方案.第一阶段确定船舶靠泊位置和时间,同时确定在每个工作段分配给每艘船的岸桥数.第二阶段建立一个基于第一阶段的详细的岸桥时间表.但是文章中假设所有的岸桥都可以在整个泊位范围内工作.这在现实中一般是不可能的.即使不考虑岸桥自身的长度和相互之间的影响,岸桥自身工作能力也限制了它们的工作范围.Zhang Canrong[11]在将连续泊位离散化的条件下,采用梯度优化法,研究了泊位和岸桥资源的协同调度问题.
总的来说,目前对于港口岸边资源的已有研究中,针对连续泊位且同时考虑岸桥资源的研究较少,且很少考虑安全作业间距、船舶离港时间、岸桥作业随机性等实际因素.
2 第一阶段:数学模型
在集装箱港口中,出口箱进场时有一个通用的规则,即将同一条船的出口箱尽量放在码头前沿的某一个区域或连续的几个区域内,船舶停靠时接近该区域,可以降低港口的作业成本,提高船舶的作业效率.因此每艘船在靠泊时都有一个自己的偏好位置.集装箱船到港后,需要给其安排码头泊位给船舶进行装卸作业,港口一般会提前1到2天得到确切的船舶靠岸时间.如果在安排船舶靠泊时,船舶到达,但没有泊位资源可以用,船舶就必须要等待一段时间.这就会产生一个等待成本.本文模型的目标就是使船舶尽可能的停靠在偏好位置上,最小化等待成本,同时尽可能减少船舶在港时间.
2.1 假设与标记
在本文中的假设有:(1)模型中允许岸桥在装卸工作时进行调整,但调整的次数是应该受到限制的,为此,假设分配给同一艘船的岸桥在一段连续的时间内,数目跟编号都不发生改变为一个操作状态.操作状态的改变,意味着岸桥进行了一次调整;(2)计划被分为多个相等的时间段,时间段越多,输出就越精确;(3)将连续泊位离散化,泊位被分为相等大小的停靠位置,泊位越多,输出越精确;(4)岸桥的开始工作后,不会被打断,即岸桥的工作在时间上是连续的;(5)船舶在接受服务后,工作不会被打断,且在工作过程中船舶不会发生移动;(6)不考虑靠离泊时间,即船舶到达后就立即接受服务,服务结束后立即离港.
模型中用到的标记:m,n,c,z,q分别表示船舶、泊位、时间、状态和岸桥的集合p表示最大操作状态数,这里取2;ek为船舶k的预计到达时间;ak为船舶k的需要装卸的作业量;hk为船舶k的长度;dk为船舶k的预计离开时间;sk为船舶k的偏好位置,即在才位置靠泊船舶装卸成本最低;mik,mak分别为船舶k服务的最小跟最大岸桥数;C0k,C1k,C2k分别为偏离偏好位置的惩罚成本,单位等待时间成本,单位在港时间成本.
决策变量的定义以及相互间关系的数学表达式略.
2.2 数学模型
对于一个靠泊计划来说,船舶的靠泊位置、靠泊时间、离泊时间确定了之后,整个靠泊的时间表就可以确定.靠泊时间取决于船舶最早的操作状态的开始时间,离泊时间等于靠泊时间+船舶在港时间,而在港时间跟分配给船舶的岸桥数成反比关系.建立泊位与岸桥优化配置模型如下.
目标函数:
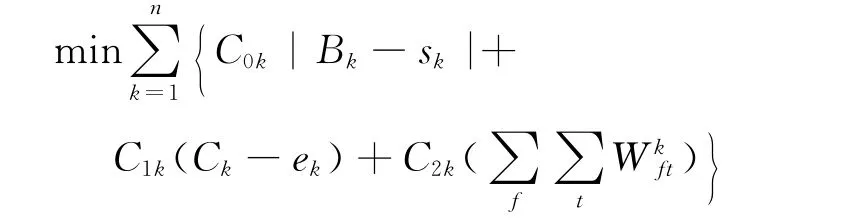
本文的目标是最小化集装箱处理成本的加权总和.目标函数中包括偏离偏好位置的惩罚成本、延迟靠泊的惩罚成本及船舶在港时间成本.
与QC相关约束条件:
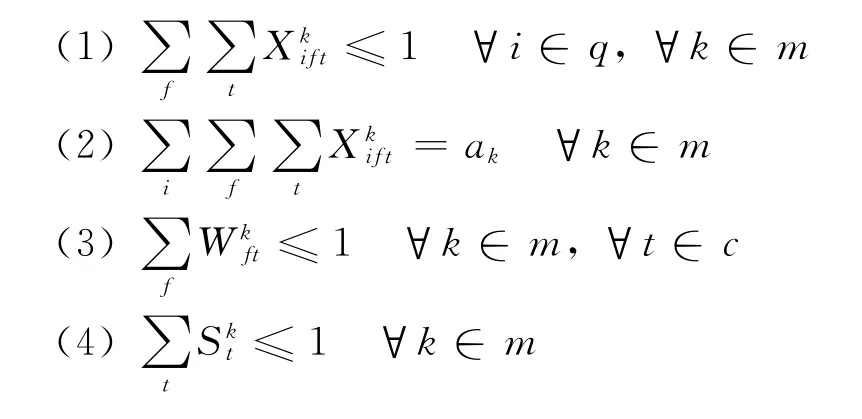

与泊位相关约束条件:

约束条件:(1)每个岸桥在一个时间段最多给1艘船工作;(2)满足岸桥的总工作量与船舶总装卸量相等;(3)分配给船舶的岸桥是连续的;(4)每个时间段每艘船舶最多有一个状态;(5)船舶从开始服务到结束服务之前不会被打断;(6)分配给每艘船的最大岸桥数约束;(7)一个状态下岸桥工作不会被打断;(8)实际到达时间与预计到达时间约束;(9)一个泊位在一个时间段内最多被一艘船占用;(10)船舶所占泊位之和等于船长;(11)船舶在接受岸桥工作时,泊位是被占用的;(12)泊位使用是连续的;(13)泊位一旦被占用,船舶离开前不会被打断.
3 第二阶段:岸桥调整启发式算法
根据第一阶段得到的岸桥在不同时间、不同状态下的工作情况,考虑到实际情况中岸桥覆盖范围的实际情况,以及在实际中,分配给船舶的岸桥是连续的,对岸桥的分配用启发式算法进行调整.为方便计算,在这里定义,如果船舶在港期间有2个操作状态,则按时间顺序,最早的状态为状态1,接下来的为状态2.具体的步骤如下.
步骤1 按船舶到达时间顺序对船舶进行编号,从1到n.
步骤2 判断是否所有船都已经分配了,分配了则结束,否则进入步骤3.
步骤3 按编号顺序选择船舶k(k从1到n).
步骤4 根据岸桥覆盖范围以及工作情况,获得船舶k状态1下的可选岸桥解空间.(因为所选岸桥编号是连续的,因此根据第一阶段已知的岸桥工作情况,最左边的岸桥确定了,顺序选择相应个数的岸桥就可以了.)从解空间中选择一个解,然后将该解从解空间中剔除更新解空间.当k=1时,状态1最终的解空间为0则无解,结束.当k不等于1时,如果无解,则判断船舶k-1是否有状态2,并令k=k-1,有状态2时,进入步骤5;没有状态2,则计入步骤2.如果有解,则判断船舶k是否有状态2.如果船舶有状态2,则进入步骤5,没有状态2,则令k=k+1回到步骤2.
步骤5 获得船舶k在状态2下可选岸桥的解空间.(解空间是在状态1已知解空间的基础上,在状态1下船舶最左或者最右的岸桥加或者减相应的岸桥数,并判断是否在状态2的时刻可以为船舶k工作,来获得的.)从解空间中选择一个解,然后将该解从解空间中剔除,更新解空间,令k=k+1,回到步骤2;如果无解,则回到步骤4.
通过上面的启发式算法就可以根据岸桥的工作范围,对岸桥的分配进行调整,进而得到确切的岸桥工作时间表.
4 数据试验
以某集装箱港口码头为例,码头岸线长度为365.72m(1 200ft),分为10个单位即10个泊位.一个时间段为2h,取12个时间段计算.船舶的长度换算成所长的泊位数,并将工作是的安全距离按船长的10%计算在内.码头设有7个岸桥,没个岸桥都有自己的覆盖范围.为了便于计算船舶的装卸作业量,按每个岸桥每小时能装卸30个集装箱,换算成一个岸桥单独完成装卸作业所需要时间,即如果ak=10则表示该船要装卸300个集装箱.在港口操作中,船舶在港时间的长短对港口影响最大,其次是等待时间,最后是偏好位置的影响.因此C0k,C1k,C2k分别取100,500,1 000.具体与船舶,岸桥相关的信息见表1~2.
利用Lingo求解第一阶段模型可以得到结果见表3.
考虑岸桥工作范围,对分配的岸桥利用第二阶段的启发式算法进行调整,得到最终的结果见表4.
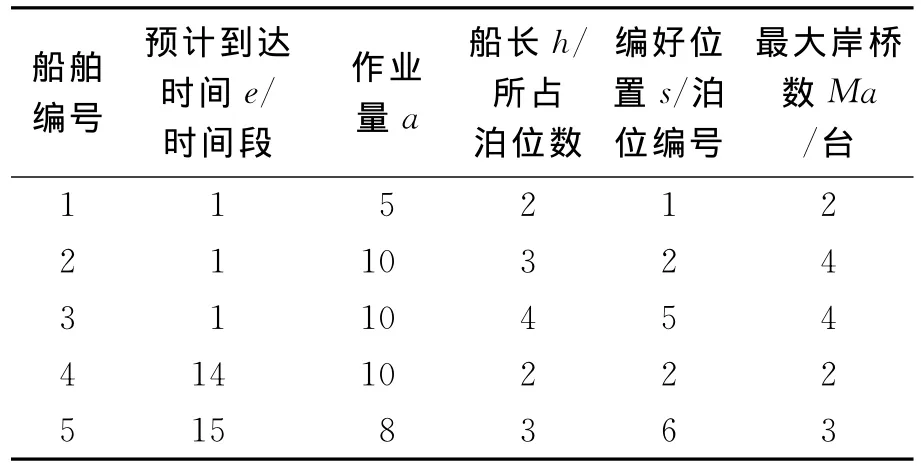
表1 船舶相关信息

表2 岸桥覆盖范围

表3 第一阶段模型计算结果
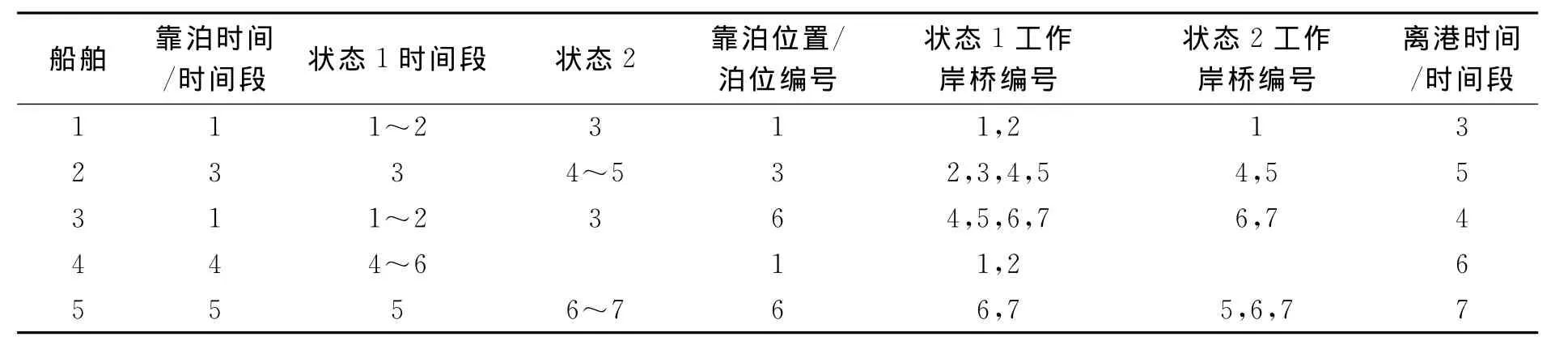
表4 岸桥调整后最终结果
通过算例,可以看到船舶2比预计达到时间晚靠泊,而第一阶段模型中分配的岸桥在考虑了岸桥覆盖范围之后,岸桥的工作是无法覆盖到船舶的,这导致了不可行解.而经过第二阶段启发式算法的调整,最终确定岸桥的分配方案,而且岸桥的分配是连续的,在同一艘船舶的不同状态间调整时也只是在原有状态的基础上加或者减一定的岸桥.更符合实际的码头操作.
5 结束语
研究了连续泊位下泊位岸桥协同调度的问题,以最小化偏好位置惩罚成本、等待时间成本与在港时间成本为目标.采用两阶段的分解算法,建立混合整数规划模型进行求解.在考虑了岸桥覆盖范围之后,使问题更加现实.但这有可能会导致第一阶段得出的结果后,在第二阶段启发式算法中无可行解.本文未能给出在第二阶段无解的情况下,如何反馈给第一阶段模型,并对第一阶段模型的结果进行调整.这将是接下来要进行的研究的工作能容.
[1]刘志雄.港口泊位调度问题粒子群优化研究[J].物流工程与管理,2010,32(8):101-103.
[2]秦 进,缪立新,陈长彬,等.时间窗限制下港口泊位优化分配问题模型[J].船海工程,2010,39(2):142-145.
[3]KIM K H,MOON K C.Berth scheduling by simula-ted annealing [J].Transportation Research Part B,2003,37(6):541-560.
[4]IMAI A,SUN X,NISHIMURA E,et al.Berth allocation in a container port:Using a continuous location space approach[J].Transportation Research Part B,2005,39(3):199-221.
[5]MONACO M F,SAMMARRA M.The berth allocation problem:A strong formulation solved by a Lagrangian approach [J]. Transportation Science,2007,41(2):265-280.
[6]LIM A,RODRIGUES B,XIAO F,et al.Crane scheduling with spatial constraints[J].Naval Research Logistics,2004,51:386-406.
[7]LEE Derhorng,WANG Huiqiu,MIAO Lixin.Quay crane scheduling with non-interference constraints in port container terminals[J].Transportation Research Part E 2008,44 :124-135.
[8]HAN Xiaole,LU Zhiqiang,XI Lifeng.A prozctive approach for simultaneous berth and quay crane scheduling problem with stochastic arrival and handling time[J].European Journal of Operational Research 2010,207:1 327-1 340.
[9]韩晓龙.集装箱港口装卸作业资源配置研究[D].上海:上海海事大学经济,2005.
[10]PARK Y M,KIM K H.A scheduling method for berth and quay cranes[J].OR Spectrum,2003,25(1):1-23.
[11]ZHANG Canrong,ZHENG Li,ZHANG Zhihai,et al.The allocation of berths and quay cranes by using a sub-gradient optimization technique[J].Computers &Industrial Engineering ,2010,58:40-50.

