有限p－群可交换的若干条件

何 美 ， 刘小川

(山西大同大学数学与计算机科学学院，山西大同037009)

有限交换群可以分解成若干有限p－群的直积，有限p－群的交换性在研究有限群中起到重要作用。本文对有限p－群的子群进行了研究，得到若干有限p－群可交换的条件。文中符号均与文献[1]、[2]中一致，p表示一个素数。

1 预备知识

定义1[1]p是素数，如果群G的任意元素的阶均为p的方幂，则称G为p－群。

引理1[2]G是有限p群当且仅当群G的阶为p的方幂。

引理2设 ｜G｜＝pn，N是G的子群，则N是G的极大子群当且仅当｜N｜＝pn－1，而且N是G的正规子群。

证明 (必要性)N是G的极大子群，则N≠G，即N＜G，从而N＜NG(N)，又N是G的极大子群，所以NG(N)＝G，于是，N是G的正规子群。

由N的极大性得到商群G/N没有非平凡子群。否则，若G/N有非平凡子群M，由群的同态基本定理知，存在M是的G非平凡子群，而且N＜M＜G，这与N是G的极大子群矛盾，所以G/N没有非平凡子群，于是G/N是p阶循环群，[G∶N]＝p，从而｜N｜＝ pn－1。

(充分性)｜N｜＝ pn－1，则 N ＜ G，若存在 M ＜ G，N ≤ M，则｜N｜｜M｜，｜M｜｜G｜，而且 p 是素数，于是M＝N，即得N是G的极大子群。

引理 3[3－6]｜G｜＝pn，｜N｜＝ p，N 是 G 的正规子群，则N ≤ Z(G)。

引理4 G是一有限p－群，且是一循环群，则G的任意阶子群均唯一。

2 主要结论

定理2[7－8]G是一有限p－群，如果G的极大子群唯一，则G是循环群。

证明 ｜G｜＝ pn，N 是 G 的极大子群，则 ｜N｜＝ pn－1，且N＜G。

取 a∈G，a∉N，令 M ＝ ＜a＞，则 M≤G。

若M＜G，则存在G的极大子群N1，使得 M≤N1，由条件，G的极大子群唯一，所以N＝N1，于是M≤N与a的取法相矛盾，即得M＝G，G是循环群。

定理3 G是一有限p－群，如果G存在p阶正规子群N，且G/N是循环群，则G是可换群。

证明 ｜G｜＝ pn，｜N｜＝ p，则 ｜G/N｜＝ pn－1。 G/N是循环群，存在a∈G，G/N＝＜aN＞。而且aN的阶为 pn－1，即∀k ＜ pn－1，有(aN)k＝ akN≠N，所以ak∉N，而 apn－1N＝N，即 apn－1

∈N。(1) 若 apn－1＝1∈N，则｜＜a＞｜＝ pn－1，令 M ＝ ＜a＞，则｜M｜＝pn－1，即M是G的一个极大子群，得M是G的正规子群。

又MⅠ N＝1，M＜MN≤G，得G＝MN＝M×N，M与N均为循环群，是可换群，所以G是可换群。

(2) 若 apn－1≠1，即 apn－1

∈N，由N是p阶循环群，知 ，｜＜apn－1

＞ ｜＝ p，即得｜＜a＞｜＝ p，G 中存在 pn阶元素a，所以G＝＜a＞是循环群是可换群。

定理4 G是一有限p－群，如果对于G的每一个元素a，都有ap＝1，则G是交换群。

证明 设｜G｜＝ pn

如果n＝0，则｜G｜＝1，G是交换群；

当n≥1时，由a∈G，ap＝1，得expG＝p，于是得G是初等交换p群，从而是交换群。

定理5｜G｜＝pn，G的任意p阶子群N均为G正规子群，G/N是交换群，而且至少存在2个p阶子群，则G可交换。

证明N均为G正规子群，由G/N是可交换，得到∀a，b∈G， [a，b]＝ a－1b－1ab∈N，即 G 的导群G′≤N 。

又若N1≠N2均为G的p阶子群，由p是素数知 N1Ⅰ N2＝ 1，而 G′≤N1，G′≤N2，所以 G′≤N1Ⅰ N2，即G′＝1，得到G是交换群。

定理6｜G｜＝pn，N是G的唯一p阶子群，G/N是交换群，p＞2，则G是循环群。

证明 (1)N是G的p阶子群，｜N｜＝p＞2，得｜G｜＞1，所以Z(G)＞1且N≤ Z(G)，由N的唯一性得N是G的正规子群，而且存在G中元素a，使得N ＝ ＜a＞。

(2)G/N 可交换，所以∀a，b∈G，[a，b]＝ a－1b－1ab∈N，即 G 的导群 G′≤N 。

(3)G中一定存在pn阶元素。

1°n＝1时，｜G｜＝p，G是循环群；2°n ＝ 2 时，｜G｜＝ p2。

若G不存在p2阶元素，必有 ∀a∈G，有ap＝1，得到 G ＝ ＜a＞×＜b＞，a，b均为 p阶元素，而且＜a＞I＜b＞＝1，从而得到两个不相同的p阶子群，这与G的p阶子群唯一相矛盾，所以G中必存在p2阶元素，亦即G是循环群；

3°n ＞ 2时，｜G｜＝ pn

假设G不存在pn阶元素，则由p群的性质，G中必存在阶数最大的元素b，设其阶为pα，α＞1。

令 M ＝ ＜b＞，N ＝ ＜a＞，则｜＜bpα－1

＞｜＝p，所以N＜M，而且b∉N。于是必存在 c∈G，c∉M，从而｜＜c＞｜＝ pβ，α≥β＞ 1，得｜＜cpβ－1

＞｜＝ p∈＜a＞ ＝ N，存在bkp∈M，使

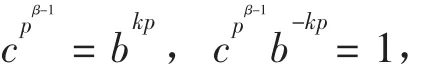
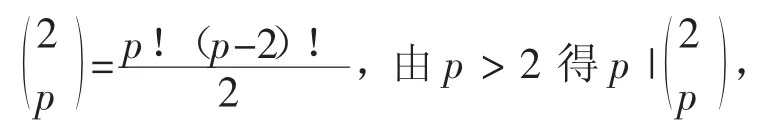
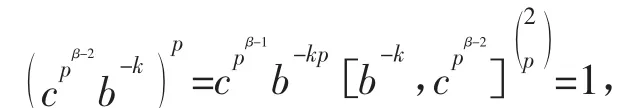
当p＝2时，此结论不成立。例如G是四元数群，只含有一个2阶子群，符合定理的条件，但G是非交换群。

对于一般的有限p－群，根据引理4及定理6有如下定理。

定理7有限p－群G是循环群当且仅当G的任意阶真子群皆是循环群且各阶子群均唯一。

[1]徐明曜.有限群导引[M].北京：科学出版社，2001.

[2]王萼芳.有限群论基础[M].北京：北京大学出版社，1987.

[3]张继荣.关于交换群的充分条件[J].咸阳师范学院学报，2002，17(6)：13－14.

[4]陈蓉，张勤海.亚循环的内交换p－群的自同构群(p≠2)[J].山西师范大学学报：自然科学版，2008，22(2)：1－5.

[5]余红宴，左可正.｜A(G)｜＝24p2q 的有限 Abel群 G 的构造 [J].徐州师范大学学报：自然科学版，2009，27(4)：14 － 18.

[6]曲海鹏.具有指数为2的循环子群的亚循环群 [J].数学的实践与认识，2009，39(4)：215－217.

[7]孙秀娟，朱艳伟.极大子群都是极小非交换群的非亚循环p－群[J].唐山师范学院学报，2009，3l(2)：37－38.

[8]Alexander Moreto.Large Orbits Of p － Groups On Characters and Applications to Character Degrees[J].Israel Journal of Mathematics，2005，146：243－251.