一类梁方程的精确可控性
王红雁
(山西农业大学信息学院,山西太谷 030800)
在本文中主要讨论下列梁方程系统

其中L是梁的长度,上标y″,yx表示关于t,x求偏导数,R1表示实数集。
首先考虑(1)所对应的齐次系统
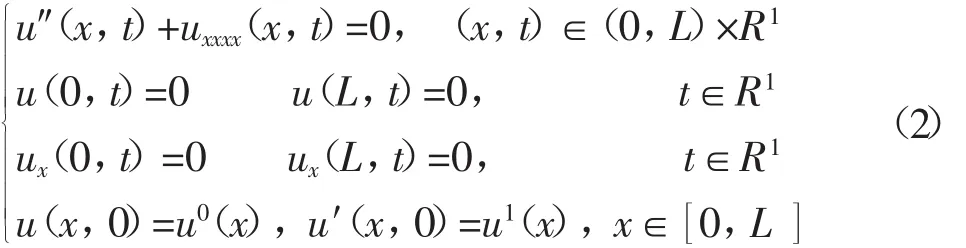
的一些性质,从而得到了两个系统在零时刻的状态空间之间的一个对应关系;最后从这映射的象解出其原象(即验证这一映射是满射),由此得到了系统(1)的精确可控性。
定义1 问题(1)是零精确可控的是指:给定T>0,若对任意(y0,y1)∈H-1[0,L]×H-3[0,L],存在一个相应的控制v∈L2(0,T),使得系统(1)的解满足:y(x,T)=0,y′(x,T)=0,x∈[0,T]。
定理 2 给定T >0,∃c=c(T)>0,使得对于(u0,u1)∈Z×Z问题(2)的解满足下列不等式:因此有一个唯一的连续线性映射

使得 L(u0,u1)=uxx,∀(u0,u1)∈Z × Z0。引入线性映射:
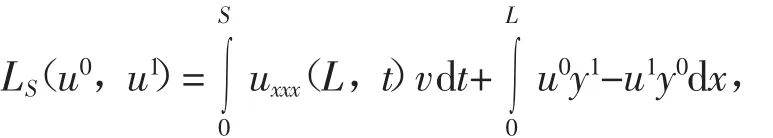
可以重新写这个恒等式为下面的形式:
LS(u0,u1)=〈(y′(S),-y(S)),(u(S)u′(S))〉X′,X
定义 3 如果(y,y′)∈(R1;H-1[0,L]×H-3[0,L])且对于∀S∈R1,(u0,u1)∈X 这一恒等映射 LS(u0,u1)=〈(y′(S),-y(S)),(u(S)u′(S))〉X′,X成立,则称(y,y′)是系统(1)的一个解。
定理 4 给定(y0,y1)∈H-1[0,L]×H-3[0,L]且则系统(1)有一个唯一的解,而且线性映射(y0,y1,v)α(y,y′)连续。
证明 由 定理2知,对于每个固定S∈R1,线性形式 LS在 X =H3[0,L]×H1[0,L]中有界,而且可以得到线性映射(u(S),u(′S))α(u0,u1)是X=H3[0,L]×H1[0,L]到自身的同构[2],因此线性映射
(u(S),u(′S))α L(Su0,u1)
接下来证明函数
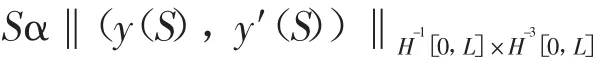
在每个有界区间上有界的。即证明对于每个有界区间 I且 S∈I,有
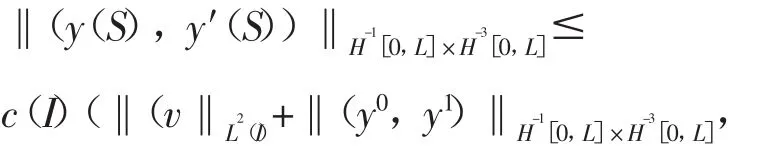
其中 c(I)由 S,v,y0,y1决定。
事实上,选择(u0,u1)∈X,引入下面的简写符号:
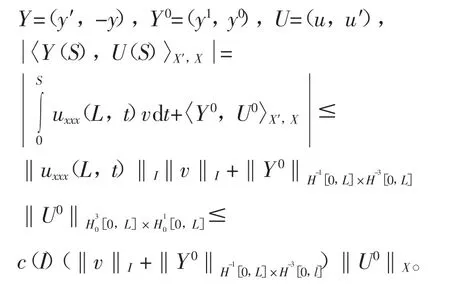
若(y0,y1)∈H-1[0,L]× H-3[0,L],且 v ∈(R1),使得 v( 0)=0 则系统(1)有一个正则解
y∈C(R1;H-[10,L])∩C1(R1;H-[30,L]),特别地有(y,y′)∈C(R1;H-[10,L]×H-3[0,L])。因为
在C(R1;H-1[0,L]×H-3[0,L])中稠,由
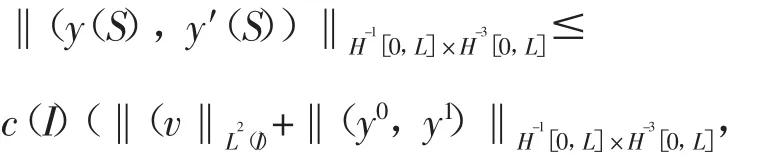
得出
(y,y′)∈C(R1;H-1[0,L]×H-3[0,L])在一般情形也成立。由知线性映射(y0,y1,v)α(y,y′)。
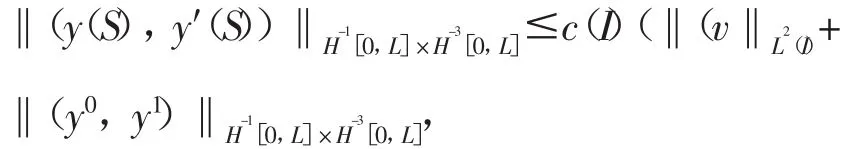
且系统(1)的解满足
y(T)=0,y′(T)=0。
次系统(2)则下列系统
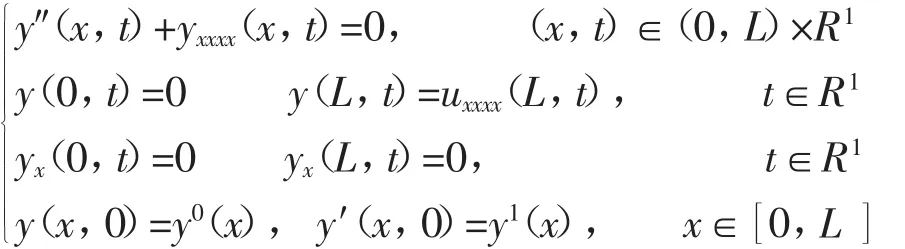
有一个唯一的解。由定理2,定理4得到Λ(u0,u1)=(y′(0),-y(0))。
[1]张恭庆,林源渠.泛函分析讲义[M].北京:北京大学出版社,2004.
[2]Komornik V.Exact controllability and stabilization[M].Paris:Chichester,1994.

