高等数学教学中易错的二个问题

罗星海

(湖北交通职业技术学院科研处，湖北武汉430079)

高等职业教育快速发展，招生规模不断增加，高等数学教学压力增大，学校聘请一些名校的博士、硕士来校上课，作为学院的中老年数学教师，在听课中发现外聘教师二个常犯的教学错误，分析出错原因，供教师教学、学生学习参考。

1 洛必达法则求极限

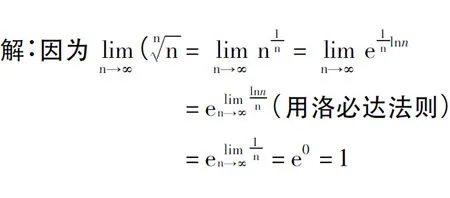
错误原因:洛必达法则误用。

定理(洛必达法则)设函数f(x)、g(x)在x0的某邻域内可导，且满足:

(2)g'(x)≠0;

正确解法如下:

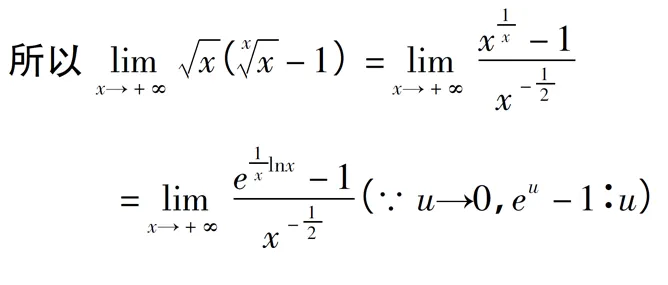
使用洛必达法则求数列极限应注意:不能直接应用该法则，可先求对应的函数极限，再根据海涅定理得到数列的极限。

海涅定理是沟通函数极限和数列极限之间的桥梁。根据海涅定理，求函数极限可化为求数列极限，同样求数列极限也可转化为求函数极限。此处，只讨论将数列极限问题转化为求函数极限问题，以便能正确使用洛必达法则。

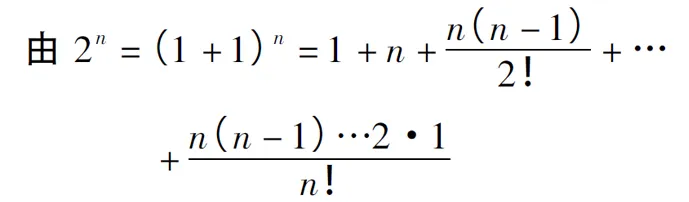
这样教学，高职学生显然无法听懂，用极限的“ε－N”定义证明数列的极限不是高职教学之重点，但采用洛必达法则求极限的方法证明，学生比较易于接受。

证法二:由洛必达法则

由海涅定理

2 定积分的定义

定义:设函数f(x)在区间［a，b］上有界，在区间［a，b］上任意插入n－1个分点

a=x0＜ x1＜ x2＜ … ＜ xi－1＜ xi＜ … ＜ xn－1＜ xn=b，把区间［a，b］分成 n个小区间:［x0，x1］，［x1，x2］，…，［xi－1，xi］，…［xn－1，xn］，各个小区间的长度分别记为

△xi=xi－ xi－1(i=1，2，…，n).在每个小区间［xi－1，xi］上，任取一点 ξi(xi－1≤ξi≤xi)，得相应的，作乘积 f(ξi)△xi(i=1，2，…，n)，得和式，当 n无限增大时，如果上述和式的极限存在，则称函数f(x)在区间［a，b］上可积，并将此极限值称为函数f(x)在区间［a，b］上的定积分.记作

错误原因:理解有误，以为n→+∞就可实现［a，b］的无限细分，“任意插入n－1个分点”与“均匀插入n－1个分点”是完全不同的，当将［a，b］平均分成n等份时，n→+∞可以保证所有△xi→0，否则，当n→+∞ 时，不能保证所有△xi→0。如，在［a，b］插入 c(a＜c＜b)，再在［a，c］内插入 n－2个分点，这样当n→+∞时，△xn=b－c不趋于0。

正确定义是:设函数 f(x)在区间［a，b］上有界，在区间［a，b］上任意插入n－1个分点

a=x0＜ x1＜ x2＜ … ＜ xi－1＜ xi＜ … ＜ xn－1＜ xn=b，把区间［a，b］分成 n个小区间:［x0，x1］，［x1，x2］，…，［xi－1，xi］，…［xn－1，xn］，各个小区间的长度分别记为

△xi=xi－ xi－1(i=1，2，…，n).在每个小区间［xi－1，xi］上，任取一点得相应的函数值 f(ξi)，作乘积 f(ξi)△xi(i=1，2，…，n)，得和式，令 λ =max{△xi}(i=1，2，…，n)，当n无限增大且λ→0时，和式极限存在，则称函数f(x)在区间［a，b］上可积，并将此极限值称为函数f(x)在区间［a，b］上的定积分.记作

例2 利用定积分概念求极限

解:设f(x)=x，在区间［0，1］内插入 n－1个分点，将区间［0，1］分成n等份，这样1，2，…，n)，在第i个小区间上取右端点为

解:函数f(x)在区间［0，1］上有界连续函数，显然可积。在区间［0，1］内插入n－1个分点，将区间［0，1］分成 n等份在第i个小区间上取右端点为于是

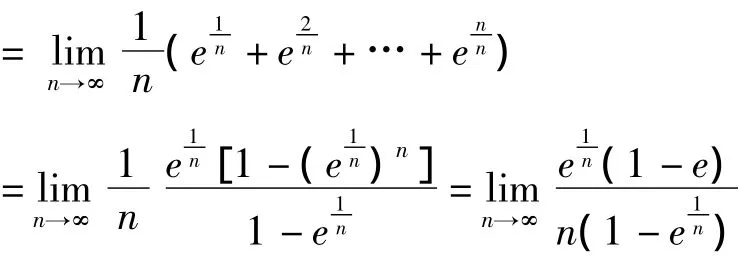
分母的极限

例2和例3可以看出，为了计算方便，一般将积分区间［a，b］分成n个区间长度相等的小区间，每个，于是，当n→∞时，也就能保证λ=Max{△xi}→0，这也就是为什么一些硕士、博士生教学时，将λ→0误解为n→∞是等效的根本原因。