缺陷钉扎导致的铁电陶瓷介电弛豫
李立本,郭惠芬,陈庆东,李庆收
(1.河南科技大学物理与工程学院,河南洛阳471023;2.南京大学固体微结构物理国家重点实验室,江苏南京210093)
0 前言
在介电常数—温度曲线上存在反常峰是铁电材料的典型特征。热力学理论和试验结果均表明:对于无缺陷的单畴铁电晶体,有奇点、不连续和尖头3种典型反常峰[1]。但是,铁电薄膜和掺杂的铁电陶瓷的介电温谱往往存在弥散的宽峰[2-8]。铁电薄膜的介电弥散被认为是一种界面效应:膜与衬底(电极)界面处的失配缺陷在膜内引起均匀的应变,会改变薄膜相变的级[9-10],或失配缺陷在膜内导致非均匀的应力场,使得相变在不同区域不同温度连续发生[11-12]。铁电陶瓷的厚度很厚,上述界面效应可以忽略。虽然颗粒间晶界对于诸如CaCu3Ti4O12这样的高介电陶瓷的介电温谱的影响巨大[13-14],但在高纯BaTiO3陶瓷却没有观察到介电弛豫现象[8]。
文献[15]曾假定铁电陶瓷中存在许多微区,每个微区的相变是一级的,但由于颗粒间的应力作用使各微区的相变温度呈高斯分布。由此,可以解释特定频率下Zr掺杂的BaTiO3陶瓷的介电温谱[8]。进而结合德拜弛豫方程,文献[16]还给出了峰值介电常数对频率的依赖关系。这种唯象模型虽在一定程度上取得成功,但假设的一致性尚需探讨,且物理本质不甚明了。铁电体的本质特征是存在自发极化,且极化取向随外加电场而变化。电极化强度对外加电场的响应是铁电畴壁运动的宏观表现。类似于超导体,把铁电畴壁的运动过程视为弹性体在随机缺陷媒质中的运动[17-18],进而量子化为电荷密度波(CDWs)在有钉扎势场中的传播[19-21],不仅物理图像清晰,而且可以从本质上理解介电常数的起源[22]。本文简单介绍CDWs理论,进而运用该理论的推论解释掺杂的钛酸钡陶瓷的试验结果。
1 CDWs理论及其在介电响应上的应用
在一个非理想晶体中,对于CDWs有两类钉扎:受库仑硬化作用影响的(弱的)集体钉扎和由亚稳态弹性形变导致的(强的)局域钉扎。集体钉扎具有大的关联长度、介电极化率和势垒高度的特征。它起源于大数量的杂质而导致的大范围(畴壁)形变,依赖于CDWs的弹性性质[19]。

系统总能量包含弹性能和库仑能两部分,均与CDWs的相移有关。能量极小的推论之一要求[22-23]

式中,ni是杂质浓度;Ea是杂质激活能;T是温度。
考虑一个孤立杂质的影响,此时只有弹性形变能。当它的势垒高度低于临界值时,它仅对集体钉扎有贡献;当它的势垒高度高于临界值时,存在亚稳态。亚稳态的弛豫导致局域钉扎的时间依赖效应。考虑低频、热激活导致的亚稳态衰减且弛豫时间满足τ=τ0e2V/T的情况,假设势垒V分布是指数型的则[22-23]


式中,ω是外加交流电场的频率。忽略其他载流子的影响,综合式(1)、式(2)和式(3)得非理想晶体的介电常数

集体钉扎和局域钉扎作用间的干涉效应,导致介电常数随温度和频率的变化呈现非单调性:对于给定的频率ωm存在一个介电峰值温度Tmax,满足关系[22-23]

解式(5)得

把式(5)代入式(4),得峰值介电常数与杂质浓度的关系满足

2 结果与讨论
文献[6]用固相反应法制备了Ba(Ti0.7Zr0.3)O3陶瓷,测得样品的介电常数随温度和频率的变化曲线如图1所示。图1表现出以下规律:(1)曲线非单调变化,存在一个介电常数峰值;(2)介电常数峰值随频率增加而减小;(3)峰值(处的)温度随频率增加而增加;(4)在极高温区,介电常数与频率无关。Y掺杂的Ba(Ti1-xYx)O3陶瓷的介电温谱也呈现了同样的规律[7]。为解释上述现象,根据式(4),且令ni=0.11,Ea=2V0,(归一化频率)相差10倍,理论模拟了Ba(Ti0.7Zr0.3)陶瓷的介电常数随温度和频率的变化曲线,如图2所示。显然,图1和图2具有相似的形态,这说明上述钉扎机制基本反映了掺杂的钛酸钡陶瓷的极化本质。
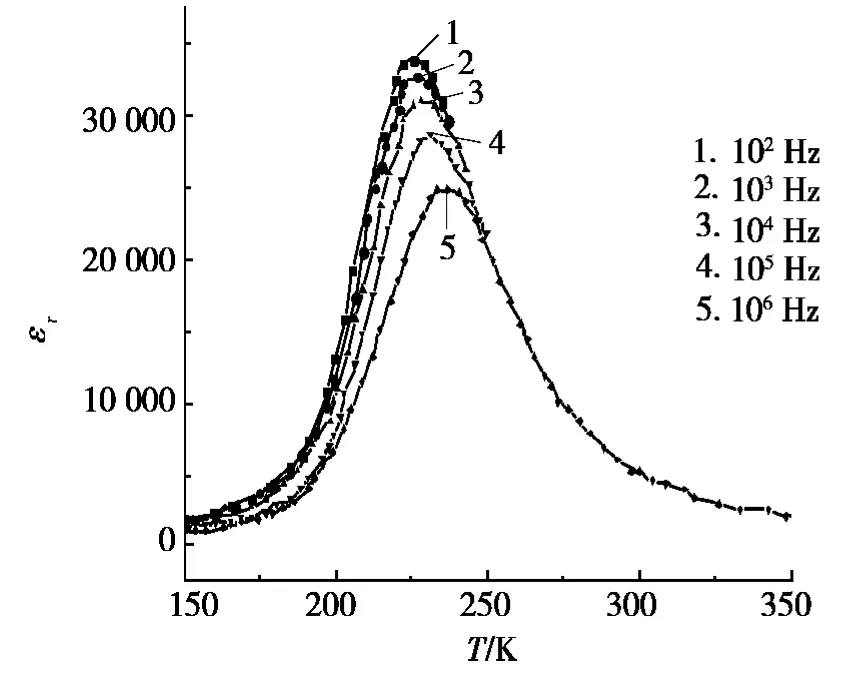
图1 Ba(Ti0.7 Zr0.3)陶瓷的介电温谱的试验结果

图2 Ba(Ti0.7 Zr0.3)陶瓷的介电温谱的理论模拟结果
文献[7]用固相反应法制备了不同比例Y掺杂的Ba(Ti1-xYx)O3陶瓷,获得了这些样品在频率为104Hz时的介电常数峰值及其相应温度对掺杂浓度的依赖关系,分别如图3和图4所示,两者均随掺杂量的增加而迅速减少。根据式(6)和式(7)并取ln(ωτ0)=-8,Ea=2V0,得到归一化介电峰值温度和峰值介电常数对掺杂浓度依赖的理论结果,分别如图5和图6所示。比较理论和试验结果可知:两者具有完全一致的变化趋势,再次说明CDWs理论可以用以描述掺杂的铁电陶瓷的介电行为。

图3 Ba(Ti1-x Y x)O 3介电峰值温度随掺杂浓度x变化的试验结果

图4 Ba(Ti1-x Y x)O3峰值介电常数随掺杂浓度x变化的试验结果

图5 归一化的介电峰值温度随掺杂浓度变化的理论模拟

图6 峰值介电常数随掺杂浓度变化的理论模拟
3 结论
掺杂的铁电陶瓷的介电弛豫特征可由陶瓷内部的缺陷对畴壁的钉扎效应来解释。CDWs理论给出的结果表明:集体钉扎和局域钉扎的竞争导致介电温谱存在峰值。峰值介电温度随频率的增加而增加,随掺杂的增加而减少;峰值介电常数随掺杂的增加而减少。这些结论与试验结果定性吻合很好。材料参数的确定及陶瓷介电损耗的理论解释有待进一步研究。
[1] Strukov B A,Levanyuk A P.Ferroelectric Phenomena in Crystals[M].Berlin:Springer,1998:95-132.
[2] Hoffmann S,Waser R.Curie-Weiss Law of(Ba1-xSrx)TiO3Thin Films Prepared by Chemical Solution Deposition[J].J Phys IV France,1998(8):221-224.
[3] Boikov Y A,Claeson T.Impact of Domain Wall Displacements on the Dielectric Permittivity of Epitaxial Ba0.5Sr0.5TiO3Films[J].JAppl Phys,2001,89(13):2052-2054.
[4] Ihlefeld JF,Vodnick AM,Baker SP,etal.Extrinsic Scaling Effects on the Dielectric Response of Ferroelectric Thin Films[J].JAppl Phys,2008,103(7):112-117.
[5] Zhang L,Zhai JW,Yao X.Dielectric Properties of Electrophoretically Deposited and Isothermally Pressed BaTiO3Thick Films[J].JAm Ceram Soc,2008,91(6):2075-2077.
[6] Yu Z,Ang C,Guo R Y,etal.Ferroelectric-relaxor Behavior of Ba(Ti0.7Zr0.3)O3Ceramics[J].JAppl Phys,2002,92(5): 2655-2657.
[7] Jing Z,Ang C,Yu Z,et al.Dielectric Properties of Ba(Ti1-yYy)O3Ceramics[J].JAppl Phys,1998,84(2):983-986.
[8] 喻惠武,朱卫利,李立本,等.锆掺杂的钛酸钡制备及介电性质研究[J].电子科技大学学报,2011,40(suppl):201-203.
[9] Pertsev N A,Zembilgotov A G,Tagantsev A K.Effect of Mechanical Boundary Conditions on Phase Diagrams of Epitaxial Ferroelectric Thin Films[J].Phys Rev Lett,1998,80(3):1988-1991.
[10] Tagantsev A K,Pertsev N A,Muralt P,et al.Strain-induced Diffuse Dielectric Anomaly and Critical Point in Perovskite Ferroelectric Thin Films[J].Phys Rev B,2001,65(1):2-5.
[11] Li L B,Zhang J,Yin Z,et al.Position-thickness-dependent Stresses and Stress-induced Diffuse Dielectric Anomaly in Perovskite Ferroelectric Films[J].Phys Lett A,2004,321:67-73.
[12] Li L B,Su L Q,Zhen ZQ,et al.Extrinsic Scaling Effects on the Dielectric Response of Grained BaTiO3Films[J].Key Engineering Materials,2010(434/435):293-295.
[13] Adams T B,Sinclair D C,West A R.Giant Barrier Layer Capacitance Effects in CaCu3Ti4O12Ceramics[J].Adv Mater,2002,14(18):1321-1323.
[14] Shao SF,Zhang JL,Zheng P,et al.Microstructure and Electrical Properties of CaCu3Ti4O12Ceramics[J].JAppl Phys,2006,99(8):084106(1-11).
[15] Smolenskii G A.Physical Phenomena in Ferroelectrics with Diffused Phase Transition[J].J Phys Soc Japan,1970,28 (suppl):26-37.
[16] 朱卫利,喻惠武,李立本,等.弛豫铁电陶瓷的峰值介电常数对频率的依赖关系研究[J].河南大学学报:自然科学版,2012,42(1):17-23.
[17] Larkin A I.Effectof Inhomogeneities on the Structure of the Mixed State of Superconductor[J].Sov Phys JETP,1970,31: 784-788.
[18] Larkin A I,Ovchinnikov Y N.Pinning in Type IISuperconductors[J].JLow Temp Phys,1979,34:409-414.
[19] Efetov K,Larkin A.Charge-density Wave in a Random Potential[J].Sov Phys JETP,1977,45:1236-1241.
[20] Fukuyama H,Lee P A.Dynamics of the Charge-density Wave I~II Long-range Coulomb Effects in an Array of Chains[J].Phys Rev B,1978,17(2):535-548.
[21] Lee P A,Rice TM.Electric Field Depinning of Charge Density Waves[J].Phys Rev B,1979,19:3970-3980.
[22] Larkin A,Brazovskii S.On Origin of the Low-temperature,Low-frequency Dielectric Susceptibility Peak in Charge and Spin Density Waves[J].Solid State Communications,1995,93(4):275-279.
[23] Brazovskii S,Nattermann T.Pinning and Sliding of Driven Elastic Systems:from Domain Walls to Charge Density Waves[J].Advances in Physics,2004,53(2):177-252.

