基于聚类建模的三维人脸识别技术研究

魏衍君， 杨明莉

(商丘职业技术学院 计算机系，河南 商丘 476000)

0 引 言

目前，由于信息采集困难、受到环境条件的约束、实现方式和手段的不足等原因，三维人脸识别技术还很不成熟[1,2].论文提出将聚类技术应用到三维人脸建模过程中，设计了一个基于三维人脸聚类建模的人脸识别系统的解决方案.针对三维人脸聚类，提出了圆锥曲线相似性三维人脸定义方法.基于三维人脸聚类建模设计了人脸识别系统的新框架，设计了与新系统对应的识别策略，解决了人脸与不同模型匹配结果无法比较的问题.本文的方法较好地提高了三维人脸建模的效果和效率.

1 聚类建模的框架

三维形变模型方法基于合成分析框架.三维形变模型的基本原理是在包含M张人脸样本的人脸空间上，将所有对应每张人脸的形状向量S和纹理向量T进行线性组合，最后生成一个形变模型：

(1)

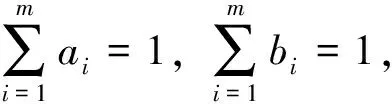
(2)

它们的协方差矩阵CS和CT可以这样计算：

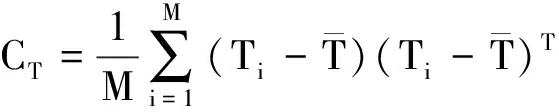
(3)

然后分别求得CS的特征值δi和特征向量Si，CT的特征值λi和特征向量ti,并按特征值由大到小的顺序取前m个最大的特征值及相应的特征向量作为变换后组合模型的基底.那么人脸空间中的一个人脸形变模型可以近似表示为：

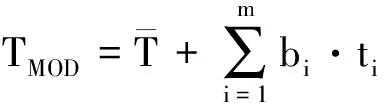
(4)

针对三维形变模型存在的问题及其解决办法，受聚类思想的启发，考虑将聚类技术应用于三维形变模型的建立.在建立形变模型之前，先对整个三维人脸库中的所有原型人脸进行聚类，然后对每一类人脸进行三维建模.这样的好处是首先使得三维人脸库的容量理论上可以无限制增长，增加模型的适用性；其次确定了模型建立时模型参数的初始值，去除了模型建立时的不确定因素；最后也是最重要的就是大大简化了模型匹配的过程，减少了迭代次数，提高了计算效率.参考三维形变模型框架，建立了三维聚类建模的主要框架，如图1所示.从图1可以看出，框架的总体结构与三维形变模型有些类似，主要的区别就是在建立形变模型之前，先对整个三维人脸库中的所有原型人脸进行聚类，然后对每一类人脸进行三维建模，最后得到一组三维形变模型.这里有两个很重要的问题需要解决.首先，要对三维人脸进行聚类，决定选用哪种特征作为三维人脸之间的相似性，并且根据这种相似性进行的聚类效果最好；其次选择最优的聚类技术，高效地进行聚类[3].

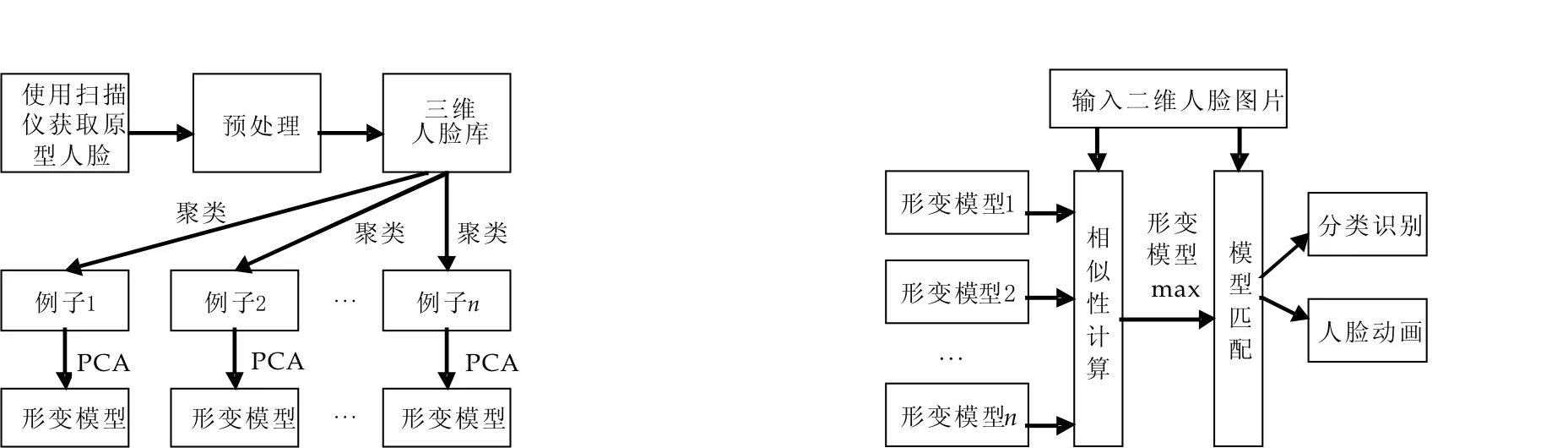
图1 三维人脸聚类建模框架 图2 人脸识别系统架构图

2 人脸识别系统框架

简单地对每个形变模型都进行模型匹配是不合适的，这样不仅增加了系统的计算量，也没有充分利用聚类建模的优势.在参照传统形变模型框架的基础上，提出了新的基于聚类建模的人脸识别系统框架，如图2所示.

在进行模型匹配之前添加了一个相似性计算模块，其主要功能是根据输入的二维图像，在n个形变模型中选择一个形变模型来进行模型匹配，当然这里不能任意选择，要按照一定的原则，这里采用的是相似性最大原则.

因为在建立这个形变模型时，是利用聚类思想先对三维人脸库进行聚类，然后在每个分类的基础上建立相应的形变模型，这里属于每个分类的三维人脸之间具有很强的相似性，所以，我们自然想到，同样按照相似性原则选择一个形变模型进行模型匹配.在现实中面临较多的是二维人脸图像识别，现在要解决的主要问题是，如何计算一张二维人脸图像与形变模型之间的相似性.

3 相似性计算

使用相似性传递聚类技术进行三维人脸的聚类，首先要解决的问题是三维人脸相似性的定义，该定义应该满足以下要求：首先计算效率高，不能为整个系统增加计算量；其次，在计算量最低的情况下提高聚类的效果，以满足实际应用的需要.

3.1 圆锥曲线相似性定义

根据光照锥理论，一个三维对象在不同光照环境下形成的所有图像可以形成一个凸多面锥，这个多面锥可以作为一个图像生成器，赋予其不同的非负系数就可以生成不同光照条件下的图像.圆锥曲线相似性定义的首要任务就是要定义一个好的度量，来描述来自同一个多面锥的图像间的相似性.

对于某一个三维人脸图像xi，可以找到一个非负的线性合成系数{bi1,bi2,…,bi(i-1),bi(i+1),…，bin}使得：

(5)

这里用到了最小二乘逼近法，对于所有的i，bii=0.

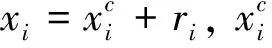
(6)

公式(5)中的系数可以用来判断xi的归属，即xi是否属于{y1,y2,…,yk}子集生成的光照锥.如果xi属于，那么对于j∈{1,2,…,k}，对应的bij应该具有相对较大的数值，其他的bij很小、或者趋于0.这样公式(5)中的线性系数就是一个很好的三维人脸圆锥曲线结构的指示器.

用矩阵B表示公式(5)中的线性系数bij，即B=(bij)，并对矩阵的每一列进行正常化处理，使得每一列的和等于1.因为一般情况下bij≠bji，也就是矩阵B不是对称的，所以可以得到需要的相似矩阵A=(B+BT)/2.

3.2 相似性的计算

Im(x,y)=(Ir,m(x,y),Ig,m(x,y),Ib,m(x,y))T

(7)

输入的二维人脸图像为：

Ii(x,y)=(Ir(x,y),Ig(x,y),Ib(x,y))T

(8)

两张人脸图像的所有像素和色阶的欧几里得距离为：

E=∑x,y(Ii(x,y))-Im(x,y))2

(9)

E的大小就反映了这两张人脸相似性的大小，E越大相似性越小，反之越大.这里的n个形变模型生成n张对应的平均人脸，E最小的平均脸对应的形变模型就是与二维输入图像最相似的形变模型.

4 三维人脸识别

三维人脸相似性的定义实际就是提取一种三维人脸特征来表示人脸，圆锥曲线相似性属于基于动态模板的特征提取，这种方法的实质是参数化的图元模型和能量函数的结合，其中能量函数的设计依据人脸的先验知识来确定，模板由三维人脸特征点的参数组成，参数可以根据环境的变化而调整，在进行特征提取时由模板的参数确定提取的面部三维特征.

三维人脸识别利用上一步所提取的面部关键特征，与数据库中已有的图像进行比较，从而得出人脸的身份.比较图像通常使用最大相似性判别法.最大相似性判别法首先匹配人脸整体的轮廓和三维空间方向；然后，在保持姿态固定的情况下，匹配脸部不同特征点.匹配时根据人脸特征向量的统计相似度来判断，相似度在一定范围之内即为识别结果.相似度的计算公式为：

(10)

其中ti是待检验样本的特征向量的第i个特征分量；pi是样本库中样本的特征向量的第i个特征分量；ki是第i个特征分量的权值；m是特征向量的维数.相似度计算不能反映脸形图像中的哪些变化量是关键的，哪些又是偶然的.因此可采用贝叶斯统计识别方法来解决这个问题.

在将上述框架应用到人脸识别时要选择一个形变模型进行模型匹配，这里提出的识别策略如下：假设这里要确定两张人脸图像A和B是否是同一个体，首先分别对这两张人脸图像与n个形变模型进行相似性计算，如果与这两张图像相似的形变模型不是同一个，那么可直接确定这两张图像不属于同一个体；如果这两张人脸图像都与同一个形变模型相似，那么再进行模型的匹配，这是得到的模型参数，具有可比性，最后根据模型参数的比较确定这两张图像是否属于同一个体.

模型匹配的过程是一个多参数的迭代优化问题，过程复杂，是形变模型中计算花销最大的处理步骤.而在实际的人脸识别系统中，大多数的情况是人脸图像不属于同一个体，如果采用如上策略，那么不需要再进行模型匹配就可以完成人脸的比较.这就大大减少了基于形变模型的人脸识别系统的总体计算量.这也正是本文提出基于聚类建模的人脸识别思想的最主要动机.

如果待处理的两张人脸图像都与同一个形变模型相似，这时就需要进行模型的匹配，这里采用了文献[5]中介绍的ICIA(Inverse Compositional Image Alignment)算法实现模型的匹配.

由两个向量之间夹角得出dA，基于极大类似分类器和线性判别分析理论得出dw：

(11)

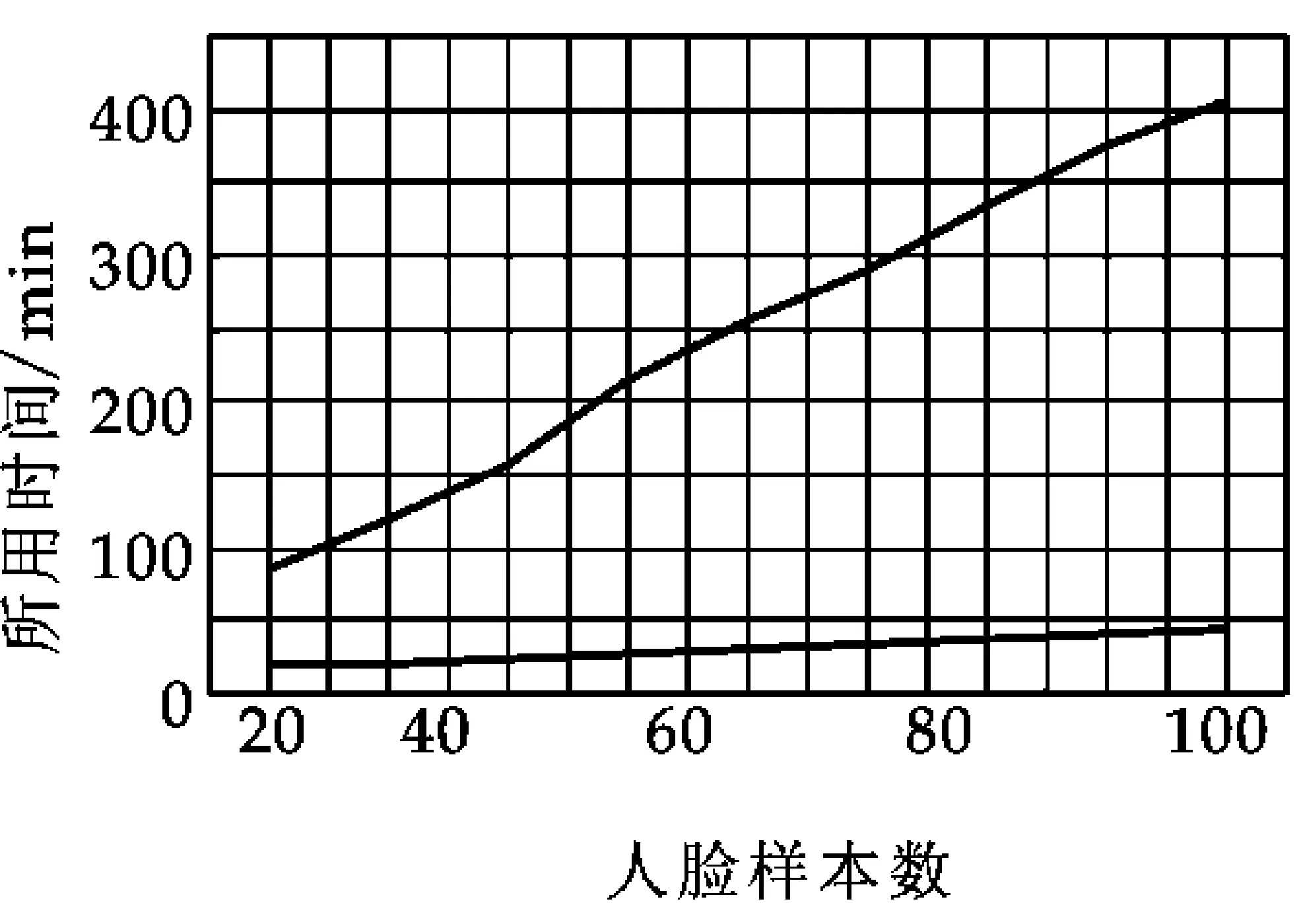
图3 所用时间比较

5 实验结果及分析

为了显示基于聚类建模的人脸识别系统相对传统形变模型在计算效率上的优势，在CMUPIE人脸数据中随机选取了100张人脸图像进行实验.实验的办法是任意从数据集中选取一张人脸图像，然后通过与数据集中其他图像进行比较，确定此人脸图像的身份，即找出与此人脸图像最接近的图片.图3显示了人脸识别系统在计算效率上与传统形变模型的差别.图3中上面一条线表示传统形变模型所用时间曲线，下面一条线是基于聚类建模的人脸识别系统时间曲线.

分析实验结果可知，基于聚类建模的人脸识别系统相对传统形变模型的系统，所用的时间差距很大，本文提出的方法在进行人脸识别时所用的时间远远少于采用传统形变模型的方法所用的时间，而且对人脸样本的数量不敏感.

参考文献

[1] 蔡雪君，谢松云，张 波．一种改进的利用五官特征的人脸识别方法[J]．计算机仿真，2009，26(11)：228-303．

[2] 王跃明，潘 纲，吴朝晖．三维人脸识别研究综述[J]．计算机辅助设计与图形学学报．2008，20(7)：819-829．

[3] Brendan J. Frey, Delbert Dueck. Clustering by passing messages between data points[J]. Science，2007，315:972-976.

[4] Mian A S，Bennamoun M，Owens R． An efficient muhimodal 2D-3D hybrid approach to automatic face recognition[J]．IEEE Transactions on Pattern Recognition and Machine Intelligence，2007，29(11)：1 927-1 943．

[5] Stan Z. Li，Anil K.Jain．Handbook of Face Recognition[M]．Springer Science & Business Media，Inc.，New York，2004．