加权回归及权函数的变换在生物量建模中的应用

郑 春 茂

（国家林业局华东林业调查规划设计院 浙江杭州 310019）

1 加权回归的概念

假定随机变量y与x满足下列模型：

式中：y为应变量；x位自变量；ε表示回归模型的误差项。采用普通回归建立模型的先决条件，误差项ε必须满足“零数学期望、独立、等方差”3个基本假设，才能获得模型的最优估计。而误差项的方差经常会随着自变量的变化，产生规律性的增加或减少，回归模型不满足“等方差”的条件，也就是回归模型存在异方差性，就不能获得最优估计。

为解决误差项ε的异方差性问题，应设法校正原有的模型，使校正后的模型其误差项具有常数方差，而模型的校正取决于方差与自变量xi之间的关系。假设 εi的方差与xi的函数呈比例关系，即：

这里2σ 是一个有限常数。于是用去除原有模型，可使新模型的误差项具有常数方差。用这种变换后的模型进行回归估计，即为加权最小二乘法，简称加权回归。

2 权函数的变换

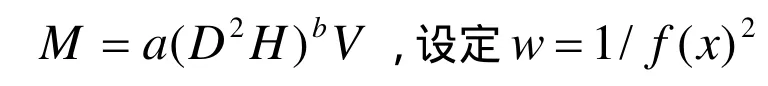
明确了权函数的结构式以后，需要将生物量模型进行变换，要求模型变换后实现系统误差（σ）最小，使用表达式描述为：

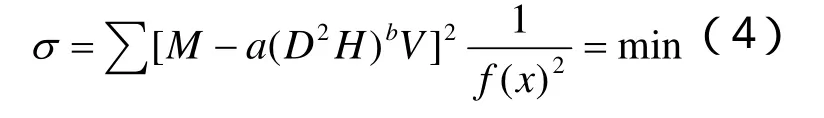
上式可以化为：

从（5）式可以看出，系统误差最小的理想情况为：

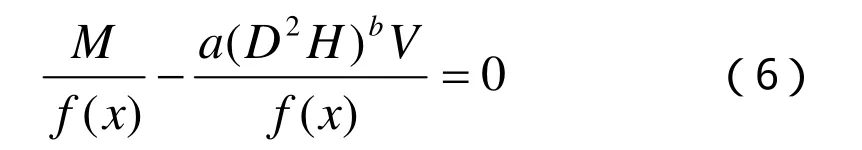
也就是满足下面表达式为最佳：

其中，f(x)为普通回归的拟合值；M为样本观察值；D为胸径；H 为树高；V为材积。

3 实例分析

生物量建模数据，按样本的部位可以分解为树干、树枝、树叶和树根，要求各部位单独建立回归模型，样本树枝的生物量因生长环境的不同，差异明显，使用普通回归的拟合结果存在异方差性，故选取2010年栎类树枝样本数据，采用加权回归估计，并对估计结果进行分析和对比。普通回归和加权回归拟合过程使用中国林业科学院编制的软件ForStat 2.0版。

3.1 回归结果

实际用于生物量建模的栎类树枝样本数量n=145，自由度p=3，使用回归模型结构式为：

其中，M表示生物量、D为样本胸径、H 为树高、V为材积。

普通回归的拟合结果如下：

附表一 普通回归拟合结果表

按普通回归拟合结果建立的回归方程，可以计算栎类树枝生物量的拟合值由此可以建立栎类树枝的回归方程：，再将生物量观察值与拟合值相除，其结果作为加权回归的观察值：

根据权函数的变换方法，可以将回归模型结构式调整为：

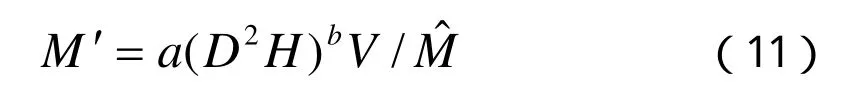
按此模型结构式进行回归计算，得到加权回归拟合结果：

附表二 加权回归拟合结果表

加权回归参数应用于普通回归方程，建立栎类树枝的加权回归方程：

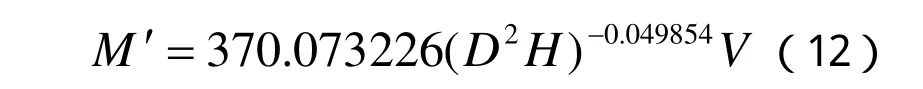
3.2 回归模型指标评价

有许多指标对回归模型的拟合结果进行评价，现选择总相对误差、总系统误差、平均相对误差、预估误差、复相关系数等作为评价指标，对普通回归和加权回归的拟合结果进行分析对比，计算公式如下：

平均相对误差：

预估误差：

复相关系数：

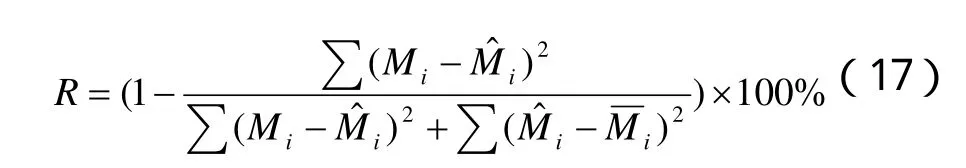
各项指标具体的计算结果如下：

附表三 回归模型评价指标

从表中分析，采用加权回归，拟合结果的总相对误差、总系统误差、平均相对误差指标不同程度下降，而预估误差、复相关系数等指标有所提高，说明使用模型本身构造权函数对模型的变换，不仅消除了普通回归存在的异方差性，同时可以提高模型拟合结果的质量。

[1] 唐守正.多元统计分析方法.北京：中国林业出版社,1984.

[2] 张会儒，唐守正，胥辉.关于生物量模型中异方差问题.林业资源管理，1999，01.

[3] 曾伟生，骆期邦，贺东.论加权回归与建模.林业科学,1999，35.