含多个时间限制因素的空车调整优化模型

周宇

（西南交通大学交通运输与物流学院，硕士研究生，四川成都 610031）

含多个时间限制因素的空车调整优化模型

周宇

（西南交通大学交通运输与物流学院，硕士研究生，四川成都 610031）

针对当前空车调整模型没有从空车流产生开始便全面地进行综合调整优化的问题，在传统空车调整模型的基础上，综合考虑了排空过程中各项时间限制因素，提出了以满足货主装车时间为重点，给定了途经中间站、技术站、装车站的时间限制条件，以满足转车时间为导向的空车调整优化模型。并对模型提出了现代启发式算法中遗传算法的求解思想，为解决在不同运输方式的衔接提供思路。

空车调整；满意装车时间；优化模型；遗传算法

空车调整问题的产生，是由于装车地装车所需空车数小于本站卸车数，卸车地卸车产生的空车数大于装车数，需对整个路网上各车站产生的空车流进行整体调整，拟定排空方向，制定空车编组方案。从一支空车流产生至这支空车流消失的整个空车调整过程，划分为“空车流产生—排空—空车流消失”三大部分。针对时间限制的空车调整问题已有了大量研究成果，如李宗平、夏剑锋以减少空车走行距离为目标，从充分利用排空站运输资源和满足时间约束2个方面进行空车调配优化；陈煜、张喜提出“到达时间窗”的概念，建立以减少空车总走行公里和广义运输成本最小化为目标的空车调整优化模型；孙焰提出矿区的最优空车分配方案，以使全矿的总落地煤最少，建立了数学定义和数学模型。以上模型的目标函数都是考虑了空车到达装车站的合理时间范围，从而降低不合理到达时间所产生的额外费用，并且有助于降低运输调配的难度。但是都没有相应反映出空车编组站或发车站的合理发车时间，无法全面地对空车调整作出从空车流产生阶段开始的综合优化。因此，本文基于装车站的货主满意装车时间范围，联系各铁路局间分界站及局管内主要编组站，推算空车合理发车时间，在分界站或中间站的通过时间限制及在技术站的合理到达时间。从空车流产生阶段全面分析排空过程各时间限制条件，强调满足货主满意装车时间限制。求解含多个时间约束寻求总消耗最少的空车调整优化模型，从而得到一个合理的空车调整计划。

1 排空过程时间限制因素及表示方法

1.1 排空过程3个阶段的时间限制因素空车调整是整个货运组织的重要一环，是货物装卸的衔接纽带，良好的衔接不仅体现在车流量的均衡分配，也体现在时间的精确对接。现在空车无法满足需求的现状，也使空车调整的时间接续性需要进一步优化。

时效性体现在空车调整的各个环节中：

1）在空车流消失端需要满足货主装车的所需时间，避免货物的堆存损失，甚至货源的流失。所以应尽量满足空车在无附加费用产生时间段内到达。

2）排空过程中排空径路所经过技术站的技术作业时间，例如由A局发往B局的一组空车在C编组站改编，在t1～t2时间范围内可编挂在a列车上，而t2～t3时间范围内a列车已开出且集结过程需要1d。则会大大增加排空时间，导致无法在货主满意时间范围内到达。对于空车直达列车则不考虑技术作业对时间的影响。

3）对于局管内空车产生端的时间影响因素，则是指的分界站或排空径路上，通过的中间站在某时段的通过能力是否影响列车的正常。空车由发车站至装车站的排空过程如图1所示。

图1 空车由发车站至装车站的排空过程

1.2 各阶段时间限制描述及时刻表示方法图1中4个车站分别为空车排空发站、途经中间站、途经需要进行编组作业的技术站、空车排空到站。

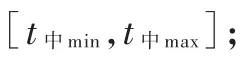
2）列车到达空车改编作业技术站的到达时间为t技到，根据历史技术站作业图表推算在t技到时刻列车到达技术站所需的编组作业时间t编。

3）由技术站发车到达空车装车站的时刻为t装，根据货主要求的货物满意装车时间范围为［t1，t2］，货物可行装车时间范围为［t装min，t装max］，当列车在［t1，t2］范围内到达则不产生存放、货损等附加费，当列车［t装min，t1］∪［t2，t装max］在范围内到达则产生额外费用c，当列车在可行装车时间范围外到达则造成车站的空车积压或货源流失。假设列车在区段内运行时间一定，则tij表示i站到j站的运行时间。所有时间点的值需满足0≤t≤24，当t≥24则用同余转化。

装车开始时刻：，

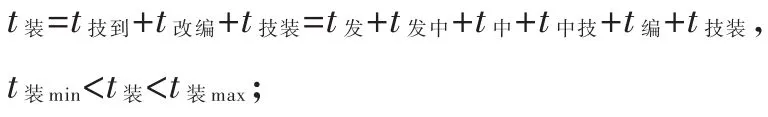
2 模型建立

2.1 空车调整模型假设条件

1）根据车流径路理论，模型假设满足空车流径路是空间对称的；

2）对于相同OD点的车流满足车流不拆散原理，即相同OD点车流径路有且仅有1条；

3）基于货主的装车需求，已知空车需求量与满意装车时间即无装车站附加费；

4）假设管内各区段均满足车流通过能力要求，且在区段内运行时间确定，其中分界站或中间站在且仅在时间范围［t中min，t中max］内满足通过能力；

5）某支空车车流满足开行空车直达列车条件，则安排开行由排空站至装车站的空车直达列车。

2.2 空车调整模型建立

目标函数为

约束条件：

2.3 模型说明目标函数包括空车运行中所消耗的费用和因时间空废造成的附加费用。时间附加费包括在技术站进行作业造成的空废时间附加费，因列车未在货主满意装车时间范围内到达装车站产生的额外费用。运输费用中c运为空车单位运输费，xij为i到j的空车数，lij为（i，j）间的运输距离。时间附加费中cij编为空车在运送j装车站需装车的货物时单位时间的运费，c装为空车未在货主满意时间内到达产生的单位额外费用。即：

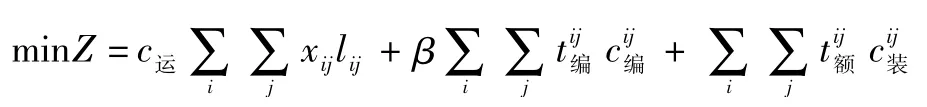
其中

3 求解算法

目标函数可以拆分为寻求运输费用最小和寻求时间附加费用最小2部分。其中运输费用中决策变量为由i站发往j站的空车数xij；时间费用中决策变量为由i站发往就j站途经边界站的技术作业时间tij中给2个目标函数分别赋予权重ω1，ω2将目标函数转化为但目标优化问题。由于本文突出对货主满意装车时间的要求，使附加时间费用的重要程度相对较高，并采用遗传算法进行求解。

3.1 编码方法采用矩阵的编码结构形式，矩阵中的每一个向量表示一个空车发车站到各装车站的决策变量信息：

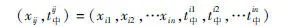
其中xij取值小于发车站的最大车流量，tij中取值在中间技术站技术作业要求时间范围内，保证初代遗传基因的质量，提高运算的效率，并采用轮盘选择法产生初始种群。

3.2 适应度函数为了满足车流量约束，分界站结束作业限制及货主满意装车时间限制，需要构造罚函数P以满足约束条件的要求。

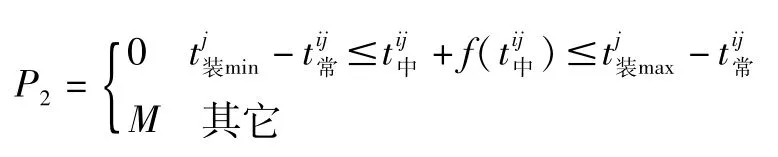
令适应度函数Fintness=Z+P1+P2，以评价种群的适应性。

3.3 交叉变异每个个体编码由2部分组成，在交叉过程中，为了使下一代在车流量与中间站技术作业时间2部分的基因，都有更大的机会可以进行交换，所以采用2点交叉。即在相互配对的2个个体编码串中随机设置2个交叉点，交换2个个体在所设定的2个交叉点之间的部分染色体。

将个体染色体编码串中的某些基因座上的基因值，用该基因座的其它等位基因来替换，从而形成一个新的个体，可以改善局部搜索能力及防止早熟现象。本文采用均匀变异，分别用符合限制条件以均匀分布选择一随机数，以某一较小概率，来替换个体编码串中各个基因座上的原有基因值。

4 结束语

本文通过分析空车流产生到空车流消失的整个过程，给出了由发车站到装车站时间限制的描述。建立了综合各种时间约束的空车调整模型，深化了空车调整的时间限制因素，使排空站可以寻求一个合理的发车时间，减少途中消耗。同时货主可以在满意装车时间内装车，减少在装车站的管理费用及货损带来的额外耗费，并且从整体考虑时间限制的优化，货主可以进一步了解何时联系托运人，可以得到最佳的服务，何时将货物运到装车站，可以使额外消耗最少。不仅使铁路空车调整计划进一步得到优化，并且使铁路公路联运方面可以得到进一步的紧密联系。

［1］李宗平，夏剑锋.基于时间约束的铁路空车调配模型与算法［J］.西南交通大学学报，2005（3）：361-365.

［2］陈煜，张喜.带时间窗空车调整问题的遗传算法研究［J］.铁路计算机应用，2007（2）：4-7.

［3］孙焰.煤矿铁路最优空车分配方案的数学模型及算法［J］.上海交通大学学报，2000（34）22-26.

U292.4+5

A

1006-8686（2012）03-0036-03