反舰导弹单发命中概率检验方法

于 录，曲宝忠，时维科

（92941部队，辽宁 葫芦岛 125001）

单发命中概率[1]作为反舰导弹武器系统的重要战技指标，反映了导弹命中预选目标的概率，它不仅取决于目标照射概率、目标捕捉概率[2]和自导命中概率，还取决于导弹的飞行可靠性[3]。反舰导弹的单发命中概率是导弹武器系统定型或鉴定试验必须检验的指标之一，如何制定科学合理的单发命中概率检验方案，最大限度地降低试验成本，全面检验武器系统的性能，对其作出客观、公正的评价，是反舰导弹武器系统定型或鉴定试验中必须解决的首要问题。

本文结合武器装备试验与鉴定工作实际，给出了二项分布序贯截尾检验[4]、二项分布假设检验[5]、二项分布Bayes 假设检验[6]和二项分布Bayes 序贯截尾检验4种单发命中概率检验方法，并对这4种检验方法进行了比较分析，确定了每种检验方法的适用原则，以指导试验方案总体设计人员制定合理的试验方案，检验导弹的单发命中概率。

1 单发命中概率检验方法

1.1 二项分布序贯截尾检验方法

设P0为单发命中概率的设计指标值，P1为使用方不希望但能接受的最低命中概率值，且P1=λP0，λ为检出比。

原假设H0：P=P0；备择假设H1：P=P1。

选取生产方和使用方双方风险α、β。设试验发数为N、试验发数截尾数为N0，当试验进行到第N0次时，若还未作出采纳或拒绝H0的决策，则定义截尾命中临界数S0。

令L0、L1为判决接受或拒绝H0的两条边界线，0h、h1分别为L0和L1的截距，k为边界线的斜率，d为鉴别比，则：

在第N0发试验完成后，根据命中数S的情况进行判断，判决图如图1所示。

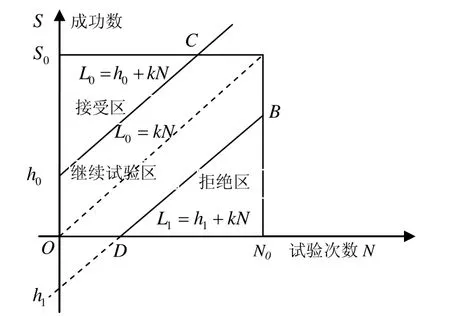
图1 判决图

2)当N＜N0且S≤L1时或当N=N0且S＜S0时，则拒绝原假设H0，即命中概率不合格；

3)否则，继续进行试验。

上述检验过程中，生产方和使用方的实际风险为：

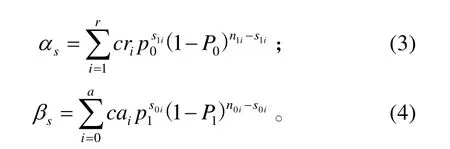
采用二项分布序贯截尾检验方法时，各参数的确定原则为：λ根据使用方不希望但能接受的最低指标 P1确定；α、β 由双方协商确定，双方风险要相当，对于检验军工产品的性能，通常α 稍大于β；N0的确定[7]关系到试验发数N的最大值，也关系到α、β，应保证α、β的规定值与实际值相近且要考虑国家的经济实力和产品的昂贵程度。

1.2 二项分布经典假设检验方法

设P0为单发命中概率的设计指标值，P1为使用方不希望但能接受的最低命中概率值，且P1=λP0，λ为检出比。

原假设H0：P=P0；备择假设H1：P=P1。

设试验发数为N，现令判决数为K，且

式中，Int表示取整函数。

若试验成功数S 满足以下条件：

则拒绝原假设H0，即命中概率不合格；否则，接受原假设H0，即命中概率合格。

双方风险为：

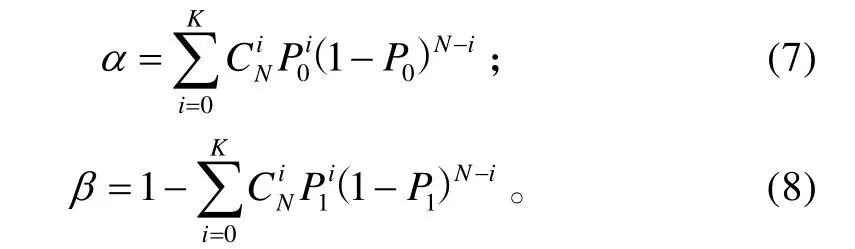
采用二项分布经典假设检验单发命中概率时，生产方和使用方的风险应相当，并小于某一值。

1.3 二项分布Bayes 假设检验方法

统计假设同1.2。

设S0为验前信息的试验成功数；0F为验前信息的试验失败数；Sn为试验结果成功数；nF为试验结果失败数，0π为原假设H0的验前概率；1π为备择假设H1的验前概率。且

若满足下面不等式：

则拒绝原假设H0，即命中概率不合格；否则，接受原假设H0，即命中概率合格。

双方风险为：

采用此方法检验单发命中概率时，双方风险应相当，并小于某一值。

1.4 二项分布Bayes 序贯截尾检验方法

统计假设同1.1。

设S为试验成功数；N为试验发数；h0为接受H0的边界线的截距；h1为拒绝H0的边界线的截距；k为边界线的斜率，且

1)若试验成功数满足

则接受原假设H0，即命中概率合格；

2)若试验成功数满足

拒绝原假设H0，即命中概率不合格；

3)否则继续进行试验。

上述检验过程中，生产方和使用方的实际风险为：

式(17)、(18)中：π0为原假设H0的验前概率；π1为备择假设H1的验前概率；cai为接受H0的组合数；cri为拒绝H0的组合数。

采用此检验方法时，采用平均风险相当原则，即 απ0=βπ1。

平均风险的大小取决于验前概率 π0，对于不同的π0，采用继续试验区宽度不变的方法，确定平均风险 απ0(=βπ1)的值。

1.5 几种检验方法的比较

在制定反舰导弹单发命中概率检验方案时，若不考虑研制试验等阶段的验前信息，可以采用二项分布序贯截尾检验方法或二项分布经典假设检验方法。但是相比较，二项分布序贯截尾检验方法的平均试验数比二项分布经典假设检验方法要小，且易于组织实施。二项分布序贯截尾检验方法和二项分布经典假设检验方法都是只考虑现场几次试验的结果，从而使鉴定的风险过高，难以作出合理的统计推断。

若定型试验有充足的验前信息[8]可以利用，可采用二项分布 Bayes 假设检验方法或二项分布Bayes 序贯截尾检验方法制定单发命中概率检验方案，以节省资源。

由于验前信息的作用，此两种方法的试验次数或平均风险较二项分布序贯截尾检验方法和二项分布经典假设检验方法小。

相比较，二项分布Bayes 假设检验方法，在π0和π1相差较大时，απ0和βπ1难以相当，相应的检验方案较偏激，难以被双方共同接受；而二项分布Bayes 序贯截尾检验方法利用了试验的过程信息，对于不同的π0，采用继续试验区宽度不变的方法，可以确定平均风险απ0(=βπ1)的值。

若某试验，仅仅检验导弹单发命中概率这一单一指标，可以用序贯截尾检验，也可以用假设检验，序贯截尾检验考虑了每次试验结果所提供的信息，可弥补在固定样本之下的统计假设检验的不足，而且有可能节省试验样本。

若某试验，要综合检验导弹的战技指标，一般不用序贯截尾检验而用假设检验。如：定型试验弹数量为10发，试验中出现了5发4中，若仅仅考核导弹的单发命中概率，则试验就可截止，此时该导弹的单发命中概率已通过检验；若综合检验导弹的战技指标，5发4中截止时，导弹飞行可靠性等指标可能就得不到检验。

2 应用实例

设某改进型导弹单发命中概率指标为0.70，研制试验为3发3中，定型试验弹数量为4发，若试验中出现4发3中，能否接受？现分别采用第1节中介绍的方法制定单发命中概率的检验方案，检验方案见表1。

表1 某导弹单发命中概率检验方案比较

从表1可以看出：通过序贯截尾或Bayes 序贯截尾检验方法计算，若出现4发3中，都需要继续进行试验，而此定型试验弹数量只有4发，试验将无法继续进行，因而利用经典假设或Bayes 假设检验方法对单发命中概率进行检验。若利用二项分布经典假设检验方法，定型试验选4发3中检验方案时，双方风险基本相当，但都较大，大于30%；若利用二项分布Bayes 假设检验方法，验前信息3发3中，定型试验选4发3中检验方案时，双方风险都小于20%，相差也不大。综合考虑，利用二项分布Bayes 假设检验方法，制定该导弹的单发命中概率检验方案为4发3中。

3 结束语

导弹武器系统定型试验时，试验方案总体设计人员要制定合理的方案检验单发命中概率。检验方案所确定的试验弹数量，既要完成单发命中概率的检验，还要完成其他战技指标的检验。因此，在制定试验方案时，要统筹兼顾，合理分配，覆盖所有战技指标范围，实现导弹武器系统的全面综合评定，并最大限度地节省资源。

[1]曲宝忠,孙晓峰.海军战术导弹试验与鉴定[M].北京:国防工业出版社,2005:52-54.

[2]于录,李瑱.目标特性对反舰导弹捕捉概率的影响[J].战术导弹技术,2010(3):44-47.

[3]刘春和,陆祖建.武器装备可靠性评定方法[M].北京:中国宇航出版社,2009:18-19.

[4]武小悦,刘琦.装备试验与评价[M].北京:国防工业出版社,2008:410-412.

[5]茆诗松,王静龙.高等数理统计[M].北京:高等教育出版社,1998:167-169.

[6]李守秀,于录,刘成生,等.GJB6671-2009 反舰导弹定型试验规程[S].2009:15-16.

[7]王正明,卢芳云.导弹试验设计与评估[M].北京:科学出版社,2010:64-65.

[8]唐雪梅,宋春雳,李荣.多状态试验数据融合处理方法[J].战术导弹技术,2011(1):1-6.