变参数锥孔装药聚能效应及其应用研究
初文华,杨文山,张阿漫,姚熊亮
(哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
随着聚能装药[1]在军事领域及民用领域中的应用越来越广泛,对于其聚能效应的理论研究以及结构设计已经日渐成为各国学者研究的热点.在军事领域中,聚能效应主要用于导弹、破甲弹、各种钻地弹等破甲战斗部;在民用领域,则主要应用于工程爆破、石油勘探、石油射孔等方面[2-3].由于应用领域的不同,这两者对于爆破效果的要求也略有不同,前者要求产生的射流在介质中能够形成一定的破甲深度和破孔直径;而后者则要求射流能够在介质中形成一定的破碎深度并产生一定的破碎体积[4].可见,对成型装药聚能效应的研究,在军事和民用上都具有十分重要的意义.
聚能装药的聚能效应具有高速性和瞬时性等特点,是一个很难从理论分析的复杂过程,并且涉及高能炸药的爆轰以及金属射流的形成和断裂2个主要问题.然而,与这2个问题相关的物质交界面和材料的大变形等问题,在采用传统的拉格朗日网格的方法进行计算模拟时,会遇到极大的困难,甚至会由于网格畸变而引起计算崩溃[5].而采用传统的欧拉网格进行计算模拟时,由于多种介质的存在导致材料界面分辨率差,很难准确模拟依赖界面几何形状的现象,如射流的形成等.相比于传统的基于网格的方法,光滑粒子流体动力学(smoothecl partide hydrodynamic,SPH)[5]方法是一种更加适于解决聚能炸药射流的数值模拟方法.它具有无网格特性和拉格朗日性质,能够克服在计算中与大变形相关的技术难题.本文应用SPH方法对聚能装药金属射流的形成及冲击靶板的过程进行数值模拟,分析研究聚能效应作用下舰船甲板结构的响应,从而为相关的军事及工程应用提供参考.
1 数值模型
1.1 控制方程
在本文的计算模型中,锥孔装药的锥形罩及靶板都采用了具有材料强度的金属结构,因此采用以下连续介质力学中的守恒方程作为具有材料强度的流体动力学的控制方程来模拟金属射流的形成过程[5]:

式中:p、ρ、e、να、χβ、σαβ、t分别代表压力、密度、内能、速度分量、空间坐标、应力张量和时间.应力张量σαβ由2部分组成,一部分是各向同性压力p,另一部分是应力偏量τ:

本文爆轰产物和金属材料分别采用了不同的状态方程.爆炸高压气体采用Jones-Wilkins-Lee(JWL)状态方程[6-7]:

式中:p为爆轰产物的压力;η为爆轰产物的相对比容,即η=ρ/ρ0;A、B、R1、R2和ω为与炸药状态有关的常数,u为高能炸药单位质量的内能.本文算例中参数取值见表1[8].
而金属材料的状态方程则采用了固体力学的Mie-Gruneisen状态方程[9]:

式中:Γ为Gruneisen常数,pH为冲击Hugoniot曲线上点的压力,其表达式为

式中:a0、b0、c0可由材料的线性状态方程Us=Cs+ SSUp计算得到.其中,Us为冲击速度,Up为粒子速度,Cs为声速,SS为曲线斜率.

表1 TNT材料参数和JWL状态方程中的参数Table 1 TNT material parameters and parameters in the equation of JWL state
1.2 本构模型
在聚能射流的形成及其冲击靶板的过程中,金属材料的本构关系和屈服强度对材料的破坏起着关键作用,直接影响强冲击下的破坏形态.在本文的计算过程中,采用Mises屈服准则[10]来判断材料的屈服状态,如下式:

本文中金属的屈服应力 σS采用 Johnson-cook材料屈服模型计算[6],其表达式为

1.3 控制方程的离散
根据SPH的核近似和粒子近似原理,对控制方程(1)进行离散,得到以下SPH形式的控制方程[5].

式中:Wij=W(x1-xj,h)为光滑函数,采用分段3次样条光滑核函数来近似控制方程.
为减少求解结果的非物理振荡和粒子之间的非物理穿透,在动量方程和能量方程中引入了Monaghan型人工粘性Πij[11-12]:

式中:影响体积粘度的参数α取为1.0,用于防止高马赫数时粒子相互穿透的参数β取值为10.
1.4 光滑长度更新
光滑长度h的选取,在SPH近似方法的计算过程直接影响到计算的精度和效率.在炸药爆轰和金属射流的形成过程中,如采用恒定的光滑长度进行数值模拟,许多细节过程将难以被模拟再现,而且数值模拟的精度也将受到极大的影响.因此本文采用Benz[13]提出的自适应动态变换方法,在每一个时间步中,对光滑长度h进行动态变换:

则有

2 数值算例
基于以上提到的SPH思想,编写了二维SPH计算程序来模拟锥孔炸药的聚能效应问题.在数值模型中,选用TNT及塑性和密度都较为理想的紫铜作为锥孔装药的组成成分,而靶板以某水面舰船的主甲板结构为攻击目标.同时还采用药量相同的方形装药,模拟其对相同结构的毁伤过程,从而对比分析不同装药形式的炸药对船体甲板的毁伤效应.2个模型的初始粒子分布如图1,模型的装药量均为7.1kg,2个模型均从装药顶端面中心起爆.


图1 相同药量不同装药形式的炸药攻击甲板基本模型及局部放大图Fig.1 Basic models of two different shaped charges with the same mass attacking the deck
2.1 计算结果分析
在图1中基本模型的基础上,图2给出了锥孔装药爆轰、射流形成以及射流对船体甲板结构的毁伤整个过程中典型时刻的粒子分布图及甲板受损严重部位的局部放大图.同时,为便于进行计算结果对比,图3给出了相同药量的方形装药爆轰对甲板结构的毁伤过程中的典型时刻粒子分布图.


图2 锥孔装药攻击甲板模型典型时刻粒子分布Fig.2 Velocity vector diagrams of shaped charge attacking deck on typical moments


图3 方形装药攻击甲板模型典型时刻粒子分布Fig.3 Velocity vector diagrams of square charge attacking deck on typical moments
从图2、3的对比可以看出,在60 μs时,锥孔装药形成的射流已经几乎穿透船体甲板,而方形装药形成的冲击波虽对甲板有一定的破坏作用,但由于纵骨等加强构件的作用,甲板结构并没有被彻底破坏,仍具有一定的强度.此后,随着时间的增加,金属射流进一步破坏甲板纵骨,并进入甲板以下,破坏其下的结构;而方形装药形成的冲击波则只是在120 μs后才基本毁坏甲板结构.从以上分析中可以看出,锥孔装药因金属射流的聚能效应,形成的破坏威力比相同药量的方形装药对结构具有更大毁伤作用.
需要补充的是,由于算例中所建立的是二维计算模型,因此加强筋在此处不能起到提高甲板结构抗弯曲性能的作用,其作用在本文中是为了验证SPH算法在计算船体板架结构时的可实现性,同时也在一定程度上增加了船体板架的局部强度.在此基础上,考虑加强筋提高板架抗弯曲性能作用的相关计算,则可以继续深入开展三维计算程序的相关研究.
从图2、3还可以看到,在连续变化过程中,加强筋在射流及冲击波的作用下,长度不断缩小,但没有发生明显的弯曲,这是由于在高强度的冲击环境下,局部结构在冲击波的传播过程中会产生近似“流体”的行为特性,此时,受到强冲击波作用的区域极有可能直接发生结构破坏而不是产生弯曲.
为更好地判断材料的破坏状态及破口形状,图4给出了2种装药爆炸冲击作用下120 μs时破口附近的等效塑性应变分布图.

图4 t=120 μs时2种装药爆炸冲击作用下破口附近等效塑性应变分布Fig.4 Equivalent plastic strain distributions of areas near the breach under impact of two different charges at the time of t=120 μs

图5 不同装药形式的模型最大压力时历曲线Fig.5 Maximum pressure-history curves of models with different charges
图5给出了2种不同装药形式的炸药破坏船体甲板过程中的最大压力时历曲线.如图所示,锥孔装药与方形装药相比,无论是在射流形成阶段的压力峰值,还是在破坏甲板过程中产生的压力峰值,都要比方形装药爆炸形成的冲击波压力峰值大很多;同时,锥孔装药的聚能效应形成的金属射流在冲击甲板时可以产生一个峰值极高的冲击压力,甚至会超过射流形成过程中压力峰值,而方形装药爆炸后,冲击波压力会随时间的推移逐渐衰减,且不会在冲击甲板的过程中再次出现压力峰值.这进一步验证了锥孔装药与方形装药相比,具有很高的聚能效应,这种聚能效应对于结构来说具有更大的破坏效果.
3 锥孔装药聚能效应的影响参数分析
锥孔装药的射流形成过程是一个极为复杂的过程.在炸药爆轰阶段,爆轰压力是影响聚能效应的主要因素,而在射流形成阶段,药型罩的锥角则是另一个至关重要的影响因素.此外,当考虑到射流的穿透深度时,炸高也是一个值得关注的关键性因素.因此,本文分别从装药长度、药型罩锥角以及炸高3个方面考虑其对锥孔装药聚能效应的影响,改变数值模型中不同参数的设置,通过计算结果的对比,分析总结出不同参数对锥孔装药聚能效应的影响规律,从而得出可获得较高聚能效应的参数设置.
3.1 装药长度对聚能效应的影响
高能炸药的爆炸是射流形成的能量来源,因此装药长度(药量)将对聚能效应产生很大的影响.本文在基本模型的基础上,分别设置装药长度为80、100、120、140、160、180mm,通过不同装药长度时的最大射流速度对比,分析装药长度对锥孔装药聚能效应的影响.
图6给出了不同装药长度情况下最大射流速度的时历曲线.从图中可以看出,在射流形成的初期,速度出现激增,此后,射流速度趋于稳定,直到其头部冲击到靶板,速度不断下降,最终再次趋于稳定.同时从图中还可以看出,随着装药长度的增加,射流形成所需的时间不断增加,而射流速度的峰值也不断增大.当装药长度小于120 mm(约3倍的装药直径)时,随装药长度的增加,射流速度峰值有明显的增大趋势;进一步增加装药长度,对于射流速度的增加没有明显的效果.分析其原因,是因为当装药长度(药量)超过一定范围后,由于稀疏波的传入,锥孔装药的有效装药量将不再增加,而是趋近于一个常数.因此,在设计锥孔装药的结构时,一定要考虑到有效装药量的问题,不能盲目的增加装药量,一般情况下,可将装药长度设置为2~3倍的装药直径,此时,既可以获得良好的聚能效应,又可以保证锥孔装药的有效装药量达到最佳.

图6 不同装药长度时最大射流速度时历曲线Fig.6 Maximum jet velocity-history curves of models with different charge lengths
图7显示了装药长度分别为 80、100、120、140 mm时,射流冲击压力的时历曲线.从图中可以看出,在装药长度小于120 mm(约为3倍的装药直径)时,随着装药长度的增加,射流冲击压力的峰值也逐渐增加,即射流对靶板的毁伤威力逐渐增大;当装药长度超过120 mm时,射流冲击压力的峰值不再增加,反而有所减小.这与图6得到的结论是相对应的.

图7 不同装药长度时射流冲击压力时历曲线Fig.7 Jet impact pressure-history curves of models with different charge lengths
3.2 药型罩锥角对聚能效应的影响
药型罩是锥孔装药形成金属射流的主要材料来源,在材料、形状以及壁厚都确定的情况下,锥角的大小必将对锥孔装药的聚能效应产生显著的影响.本文在基本模型的基础上,分别采用锥角大小为4个不同值的锥孔装药模型进行计算模拟.图8、9分别给出了不同模型的最大射流速度时历曲线以及射流冲击压力时历曲线.

图8 不同锥角时最大射流速度时历曲线Fig.8 Maximum jet velocity-history curves of models with different cone angles

图9 不同锥角时射流冲击压力时历曲线Fig.9 Jet impact pressure-history curves of models with different cone angles
从以上两图中可以看出,射流冲击速度和冲击压力都随药型罩锥角的增大而逐渐减小.因此要想提高锥孔装药射流的聚能效应,可以从减小药型罩的锥角方面来考虑.但与此同时也必须考虑到,随着锥角的增大,虽然射流的穿透深度将有所降低,但是其破孔直径将会增大.从图中可以看出,当锥角增大到一定范围之后,继续增大锥角,射流的冲击压力将不会有明显的降低,因此,若想获得较大的破孔直径,可以考虑适当的增大药型罩的锥角.
3.3 炸高对聚能效应的影响
所谓“炸高”,是指在锥孔装药爆炸的瞬间,药型罩的底端至靶板的距离.随着金属射流的向前运动,射流将在拉应力的作用下不断被拉长,这将在一定程度上有利于穿透深度的增加.但当炸高过大时,由于射流在被拉伸的过程中,出现拉应力大于射流内聚力的现象,射流将会被拉断而导致冲击速度和压力的降低,从而使穿透深度大大降低.
图10给出了锥孔装药的炸高与金属射流穿透速度之间的关系曲线.从图中可以看出,炸高对射流穿透速度的影响很大.在装药量、锥角等其他参数一定的情况下,锥孔装药存在一个最有利炸高[1],即当炸高设置为最有利炸高时,射流的穿透速度将达到最大值,相应的锥孔装药的聚能效应也达到最高.当炸高小于最有利炸高时,射流的穿透速度随炸高的增加而增加;当炸高超过最有利炸高后,继续增加锥孔装药的炸高,射流的穿透速度不会继续增加反而逐渐下降.产生这一现象的主要原因为:1)射流刚开始形成的阶段,由于冲击波的传播和推动,金属射流的速度不断增大,此时,若炸高较小,则在射流速度还没有达到最大值时,便由于靶板的阻挡及稀疏波的传入,使得射流对靶板的穿透速度迅速下降; 2)随着炸高的增加,射流在到达靶板前的加速时间增大,则其冲击靶板的速度也相对提高;3)另一方面随炸高的增加,射流将产生径向分散和摆动,甚至延伸到一定程度后出现断裂,此时射流的冲击速度将大大降低,进而其对靶板的穿透速度也迅速减小.
从图10中可以看出,当采用紫铜作为锥孔装药的药型罩材料时,最有利炸高约为锥孔直径的1.5倍左右,即考虑到炸高这一影响因素时,若要获得较高的聚能效应,应将锥孔装药放置在距离目标约1.5倍锥孔直径的位置处.
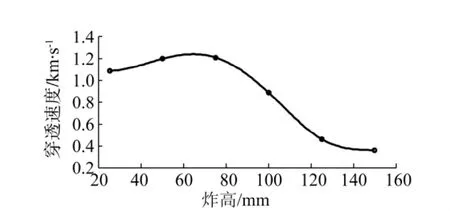
图10 射流穿透速度与炸高的关系曲线Fig.10 Jet penetration velocity changing with height of burst
4 结论
本文基于光滑粒子流体动力学(SPH)方法,模拟研究了锥孔装药的聚能效应及其影响参数,通过计算分析,得出了以下结论:
1)光滑粒子流体动力学(SPH)方法可以很好地再现锥孔装药从炸药爆炸—金属射流的形成—射流冲击靶板的整个过程,并且能够较为精确地模拟出锥孔装药的聚能效应.高能炸药爆炸产生的爆轰波挤压药型罩使之形成高能射流,在射流穿透靶板的过程中,会出现失稳(颈缩和断裂)现象,其压力值大大减小.
2)锥孔装药与方形装药相比,在相同药量的情况下,可以对船体甲板结构产生更大的毁伤效应,进一步验证了锥孔装药的聚能效应及其实用价值.
3)随着装药长度的增加,射流形成所需的时间不断增加,而射流速度的峰值也不断增大.当装药长度小于约3倍的装药直径时,随装药长度的增加,射流速度峰值有明显的增大趋势;进一步增加装药长度,对于射流速度的增加没有明显的效果.
4)金属射流的冲击速度和冲击压力都随药型罩锥角的增大而逐渐减小,但随着锥角的增大,虽然射流的穿透深度将有所降低,其破孔直径将会增大.当锥角增大到一定范围之后,继续增大锥角,射流的冲击压力将不会有明显的降低.
5)在装药量、锥角等其他参数一定的情况下,锥孔装药存在一个最有利炸高,当炸高小于最有利炸高时,射流的穿透速度随炸高的增加而增加;当炸高超过最有利炸高后,继续增加锥孔装药的炸高,射流的穿透速度不会继续增加反而逐渐下降.当采用紫铜作为锥孔装药的药型罩材料时,最有利炸高约为锥孔直径的1.5倍左右.
[1]王志军,尹建平.弹药学[M].北京:北京理工大学出版社,2005:18-21.
[2]荀扬,晏麓晖,曾首义.聚能装药技术研究进展综述[J].科学技术与工程,2008,8(15):4251-4257.
XUN Yang,YAN Luhui,ZENG Shouyi.Process of the shaped charge technique[J].Science Technology and Engineering,2008,8(15):4251-4257.
[3]纪国剑.聚能装药形成射流的仿真计算与理论研究[D].南京:南京理工大学,2004:1-2.
JI Guojian.Emulation calculation and theoretical research on the jet formation of shaped charges[D].Nanjing:Nanjing University of Science and Technology,2004:1-2.
[4]石连松,宋衍昊,陈斌.聚能爆破技术的发展及研究现状[J].山西建筑,2010,36(5):155-156.
SHI Liansong,SONG Yanhao,CHEN Bin.The development and research status quo of accumulative blasting technology[J].Shanxi Architecture,2010,36(5):155-156.
[5]LIU G R,LIU M B.光滑粒子流体动力学——一种无网格粒子法[M].韩旭,杨刚.强洪夫,译.长沙:湖南大学出版社.2005:65-70.
[6]迈耶斯.材料的动力学行为[M].张庆明,译.北京:国防工业出版社,2006:34-39.
[7]陈郎,龙新平,冯长根,等.含铝炸药爆轰[M].北京:国防工业出版社,2004:23-28.
[8]SHIN Y S,LEE M,LAM K Y,et al.Modeling mitigation effects of water shield on shock waves[J].Shock and Vibration,1998,5(4):225-234.
[9]LIBERSKY L D,PETSCHECK A G,CAMEY T C,et al.High strain Lagrangian hydrodynamics——a three-dimensional SPH code for dynamic material response[J].Journal of Computational Physics,1993,109(1):67-75.
[10]杨桂通.弹塑性力学引论[M].北京:清华大学出版社,2004:18-23.
[11]LATTANZIO J C,MONAGHAN J J,PONGRACIC H,et al.Controlling penetration[J].SIAM Journal on Scientific and Statistical Computing,1986,7(2):591-598.
[12]MONAGHAN J J.On the problem of penetration in particle methods[J].Journal of Computational Physics,1989,82(1):1-15.
[13]BENZ W.Smoothed particle hydrodynamics——a review[C]//NATO Workshop.Les Arcs,France,1986.

