用量子蚁群算法求解大规模旅行商问题
李 煜, 马 良
(1.上海理工大学管理学院,上海 200093;2.河南大学管理科学与工程研究所,开封 475004)
蚁群算法是一种来自生物界的随机搜索寻优方法,由意大利学者Colorni等[1-2]于20世纪90年代初期通过模拟自然界中蚂蚁的寻径行为,而提出的一种基于种群的启发式仿生进化算法,并得到了广泛的应用[3-4].但蚁群算法在较大规模问题中计算时间偏长、运算精度低.本文将在基本的蚁群算法中融入量子计算理论,以进一步提高搜索效率和搜索精度.
量子优化是由量子计算和量子信息论发展而来的,20世纪80年代初Benioff和Feynman提出了量子计算的概念,随后Shor于1994年提出基于量子Fourier变换的大数质因子分解算法,大数质因子求解问题是公认的NP(non-deterministicpolynomial)问题,Shor算法将大数质因子求解转换为P(polynomial)问题.Grover于1996年提出无序数据库的量子搜索算法,该算法则提供了经典算法的根方加速,从此,量子计算以其独特的计算性能引起了广泛的瞩目,并迅速成为研究的热点[5-7].世界首台通用编程量子计算机已经于美国面世[8],其可在进一步改进后应用于密码破译等方面.将量子计算技术应用于优化理论中,称为量子优化算法,可以解决经典方法难以解决或无法解决的许多问题.量子蚁群算法是一种基于量子优化原理的新的优化方法,其将量子优化和蚁群寻优相结合,提高了旅行商问题(TSP)的运算精度.本文首先结合TSP给出量子蚁群算法的原理,然后用数值实验说明其有效性.
1 量子蚁群算法
1.1 TSP的一般描述
TSP是一个典型的优化组合问题,已被证明属于NP完全问题.对于TSP的求解,一直以来都是学术界研究的热点,精确算法主要有线性规划算法、动态规划算法和分支定界算法,但这些精确算法是指数级的,所能求解的问题规模非常有限,对n个城市而言,可能的路径总数为n!/2n,随着n数的增加,路径数将急剧增长.由于现实中这些问题在许多领域都有着广泛的应用,因而寻找其实际而有效的算法就显得颇为重要.尽管有指数级的算法可作精确求解,但随着它们在大规模问题上的失效(组合爆炸),人们退而求其次,转向寻找近似算法或启发式算法.经过几十年的努力,取得了很大的进展[9-12].
TSP在图论意义下又常常被称为最小哈密顿圈问题,这里用数学的语言来进行描述.
记G=(V,E)为赋权图,V={1,2,…,n}为顶点集,E为边集,各顶点间的距离cij已知,cij>0,cij=∞,i,j∈V.设
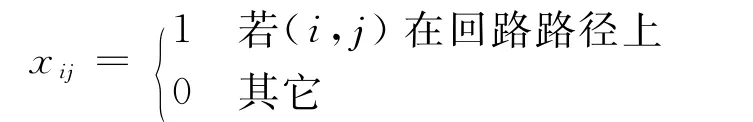
则经典TSP的数学模型为
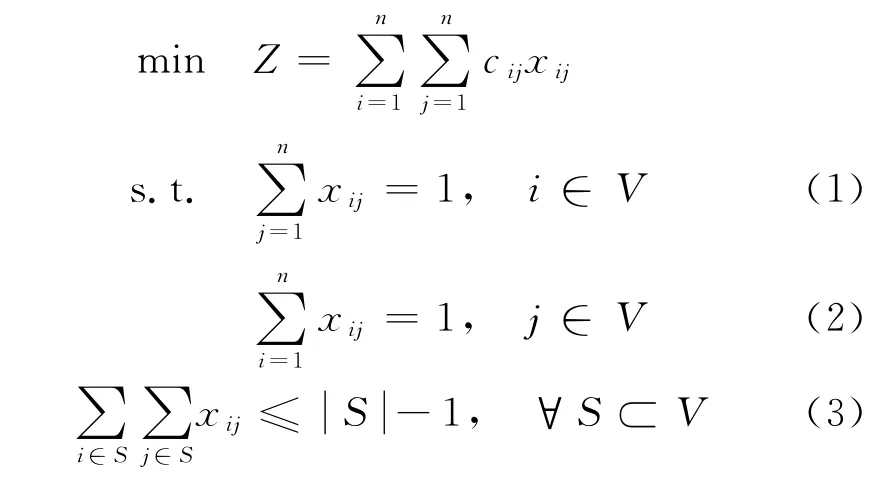
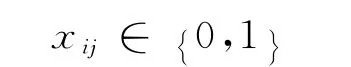
式中,Z为目标函数值;|S|为集合S中所含图G的顶点数.
约束(1)和(2)意味着对每个点来说,仅有一条边进和一条边出;约束(3)则保证了没有任何子回路解的产生.于是,满足约束(1)~(3)的解构成了一条哈密顿回路.
为简便起见,本文中假定所考虑的都是欧氏意义下的完全图;否则,可通过求任意两点间的最短路转化为等价的完全图形式.
1.2 量子算法
量子算法是一种新发展起来的概率进化算法,它基于量子计算原理,利用量子计算的一些概念和理论,如量子位、量子叠加态等.量子比特是量子计算中保存信息的最小单元,一个量子比特可能处于,也可能处于,还可以是两种状态的线性叠加[7,13].因此,一个量子位可表示为
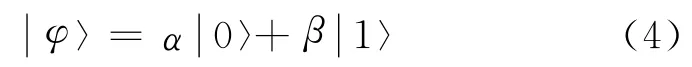
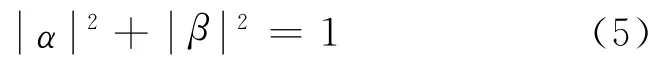
一个具有m个量子比特位的系统同时表示2m种状态,可以描述为
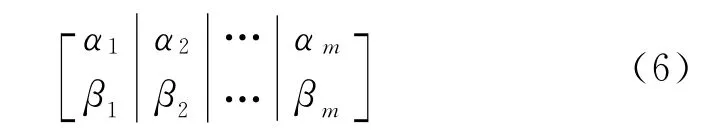
1.3 蚁群算法
蚁群算法(ant colony algorithm)是一种新颖的仿生算法,它抽象了自然界蚂蚁的群体行为,吸收了昆虫王国中蚂蚁群体的行为特性,用蚂蚁群在搜索食物源的过程中所体现出来的寻优能力来解决一些离散系统优化中的困难问题.该方法目前已经成功地应用于很多NP完备的组合优化问题.
蚁群算法的转移概率是一个非常重要的因素,它体现了人工蚂蚁在移动时的寻优特性,应用在算法中主要体现在两个方面,即信息素轨迹强度和距离,它们分别以一定的权重影响着转移概率的值.
按照TSP的约束,在蚂蚁的周游完成以前只能访问未曾到过的节点,设蚂蚁的数量为m,系统初始时将m只蚂蚁随机放在n个节点上,并设置了每边的初始信息素浓度.为此设定一个禁忌表t[m][n].其中,t[k][f]表示蚂蚁k在时刻t以前走过的点.蚂蚁的一次周游构造了问题的一个可行解.当m只蚂蚁都完成一次周游后,便在各自经过的路径的每一条边上留下信息素.若算法经过N次循环后停止,则基本蚁群算法的时间复杂度为Ο(N·m·n2).在实验中,m一般取值与n为同一数量级,因此,整个算法的复杂度为Ο(N ·n3).
位于i处的蚂蚁k移至其邻域中结点j处的概率为
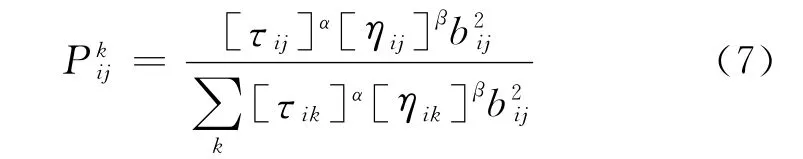
式中,ηij为边弧(i,j)的能见度(visibility),即1/dij;τij为边弧(i,j)的轨迹强度(intensity);α为轨迹的相对重要性,α≥0;β为能见度的相对重要性,β≥0;bij为边弧(i,j)量子信息强度.
给定城市元素的集合C={c1,c2,…,cn},C中任意排列组合L={(c1…,ci,…,cj,…,cn),ci∈C,i,j=1,2,…,n},L为路径(i,j)的长度.
信息素强度的更新方程为
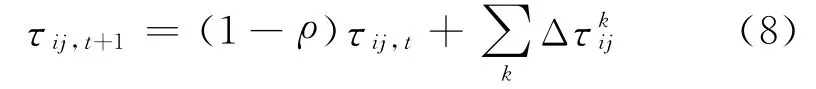
式中,τi,j,t+1,τij,t分别为第t+1次和t次迭代的边弧(i,j)的轨迹强度;Δτkij为蚂蚁k在边弧(i,j)上留下的单位长度轨迹信息素数量,ρ为信息强度的挥发性,0≤ρ<1.
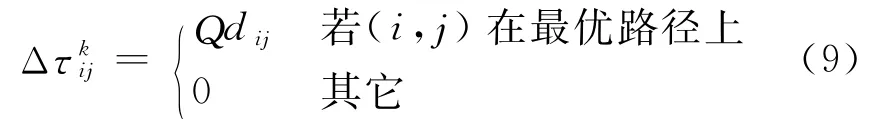
式中,Q为蚂蚁所留下轨迹数量的一个常数.
1.4 量子蚁群算法
量子蚁群算法集量子计算和蚁群算法的优点于一身,对它们取长补短,同基本的蚁群算法相比具有更好的搜索性能.量子算法可以根据不同的问题设计不同的量子门使得算法搜索到最优解.量子门的设计有多种形式,但由于概率归一化的要求,变换矩阵必须满足酉正矩阵,酉性限制是对量子门的唯一限制.常用的有非门、受控非门、Hadamard门及量子旋转门等.量子门是实现算法进化操作的执行机构,通过量子门算子使量子比特的概率幅发生变化,推动量子个体向最优解方向演化,本文设置的量子旋转门为
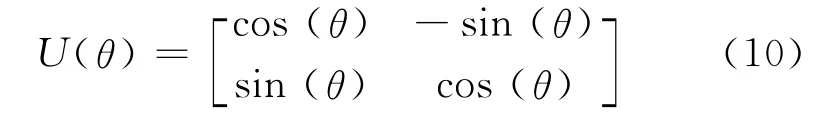
式中,θ为旋转的角度.
通过不断地更新量子旋转门U(θ)来更新量子比特qj,不断地生成新的解X,比较解X的函数值,可以得到最好解b.量子旋转门的调整方式可定义为
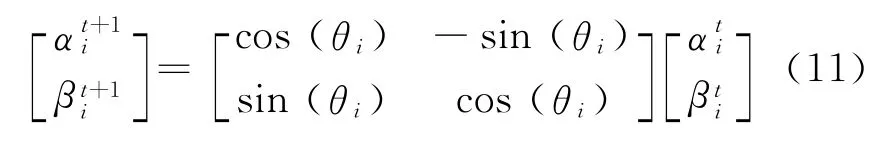
旋转角的幅值直接影响算法的收敛速度和搜索能力.如果幅值过大,会导致早熟;如果幅值过小,会是收敛速度减慢.其值一般在0.001π~0.05π之间.其大小和方向根据关系式θi=Δθis(αi,βi)来确定,s(αi,βi)是决定θi的旋转方向的符号函数,Δθi是旋转角度的大小.
由上述定义可知,量子蚁群算法的性能受到初始值的影响.在每一次迭代中,算法将会更新蚂蚁的信息素,同时要进行量子门旋转来更新量子比特,使得算法不断地改进最优解.
量子蚁群算法主要步骤描述如下:
步骤1 nc为迭代次数,nc←0;
对τij和Δτij进行初始化;
将m个蚂蚁置于n个顶点上.
步骤2 将各蚂蚁的初始出发点置于当前解集中;
对每个蚂蚁k(k=1,2,…,m)按转移概率pkij及其它要求移至下一顶点j;
将顶点j置于当前解集中.
步骤3 计算各蚂蚁的目标函数值Zk,k=1,2,…,m;
记录当前的最好解.
步骤4 按更新方程修改轨迹信息素强度.
步骤5 按量子旋转门来更新量子信息.
步骤6 对各边弧(i,j),置Δτij←0;nc←nc+1.
步骤7 若nc小于预定的迭代次数且无退化解(即找到的都是相同解),则转步骤2.
步骤8 输出目前的最好解.
2 数值实验
为验证量子蚁群算法的有效性,采用网上公布的标准问题库TSPLIB中的实例(http://www.iwr.uniheidelberg. de/groups/comopt/software/TSPLIB95/tsp/).在Windows XP下用Delphi 7.0编制程序进行了计算.各种参数的设定如下:蚂蚁数目为50,α取值为1~2,β取值为1~3,ρ=0.7,量子比特初始化为即所有的路径被选择的概率相等,并使用三边交换算法(3-OPT)进行邻域优化.
现介绍部分问题得到的结果.B1为本算法求得的最优解,B2为TSP库中公布的最优解的值,同最好解的偏差率R=(B1-B2)/B2,表1中问题名称的数字为结点总个数,且从小到大显示.这里给出本算法求解部分的详细情况,其余只给出结果,如表1所示.
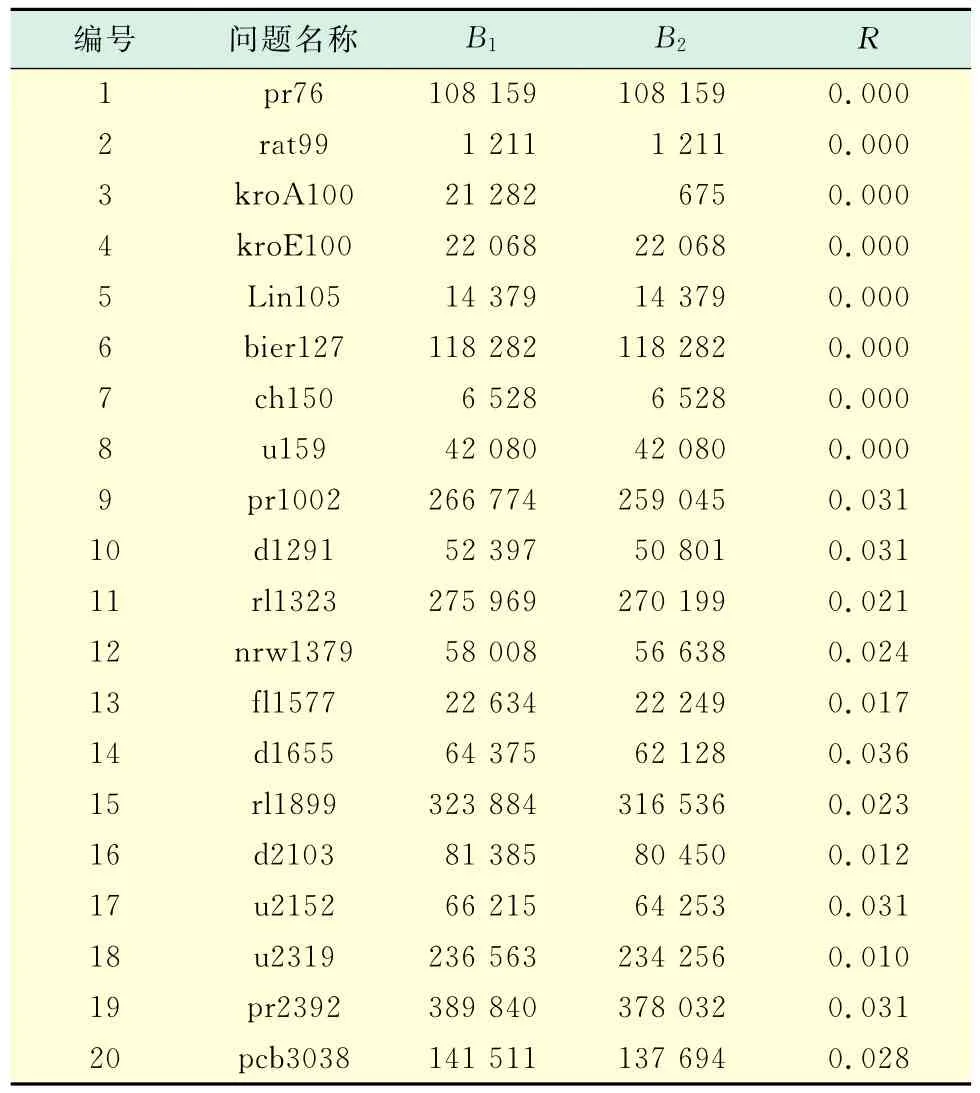
表1 计算结果Tab.1 Calculation results
实例1 文件名:St70,其中,结点个数N=70,B2=675,本算法求解的结果为
蚂蚁回路总长B1=675,等于公布的最好解.
蚂蚁回路路径P=1 36 29 13 70 35 69 31 38 59 22 66 63 57 15 24 19 7 2 4 18 42 32 3 8 26 55 49 28 14 20 30 44 68 27 46 45 25 39 61 40 9 17 43 41 6 53 5 10 52 60 12 34 21 33 62 54 48 67 11 64 65 56 51 50 58 37 47 16 23.
实例2 文件名:Berlin52,其中,N=52,B2=7 542,本算法求解的结果为
蚂蚁回路总长B1=7 542,等于公布的最好解.
蚂蚁回路路径P=1 22 31 18 3 17 21 42 7 2 30 23 20 50 29 16 46 44 34 35 36 39 40 37 38 48 24 5 15 6 4 25 12 28 27 26 47 13 14 52 11 51 33 43 10 9 8 41 19 45 32 49.
从表1中的数据可以看出,量子蚁群算法在TSP求解过程中总体效果良好,部分算例的计算结果已达到公布的最优解,算法结果与最好解的误差率很小,说明该算法有较好的优化性能.
3 结束语
量子蚁群算法建立在量子的态矢量表示的基础之上,将量子比特的概率幅表示应用于人工蚂蚁的位置,并利用量子逻辑门实现量子比特的更新操作,从而实现了目标的优化求解.根据旅行商问题的特点,利用量子比特的特点结合蚁群算法,给出了量子蚁群算法的描述,通过大量的数值测试探讨了算法的求解性能,从数值模拟结果来看,本文给出的量子蚁群算法可以较快、较好地找到问题的最优解或近似最优解,是求解TSP的一个新的可行手段.
[1] Dorigo M,Maniezzo V,Ccolorni A.The ant system:Optimization by ant colony cooperating agents[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B,1996,26(1):29-41.
[2] Dorigo M,Gambardella L.Ant colony system:A cooperative learning approach to the traveling salesman problem[J].IEEE Transanctions on Evolutionary Computation,1997,1(1):53-66.
[3] 马良,项培军.蚂蚁算法在组合优化中的应用[J].管理科学学报,2004,4(2):32-37.
[4] 马良,朱刚,宁爱兵.蚁群优化算法[M].北京:科学出版社,2008.
[5] Hey T.Quantum computing:An introduction[J].Computing &Control Engineering Journal,1999,10(3):105-112.
[6] Han K H,Kim J H.Genetic quantum algorithm and its application to combinatorial optimization problem[C]//IEEE Proceedings of the 2000Congress on Evolutionary Computation.2001:1354-1360.
[7] Han K H,Kim J H.Quantum-inspired evolutionary algorithms with a new termination criterion[J].IEEE Transactions on Evolutionary Computation,2004,8(2):156-169.
[8] Hanneke D,Home J P,Jost J D,et al.Realization of a programmable two-qubit quantum processor[J].Nature Physics,2010,6:13-16.
[9] 孙聪,赵新超.旅行商问题研究及混合粒子群算法求解[J].计算机工程与应用,2009,45(25):38-40.
[10] 马良.求解最小比率TSP的一个算法[J].系统工程,1998,16(4):62-65.
[11] 马良,蒋馥.多目标旅行售货员问题的蚂蚁算法求解[J].系统工程理论方法应用,1999,8(4):23-27.
[12] 王宇平,李英华.求解TSP的量子遗传算法[J].计算机学报,2007,30(5):748-755.
[13] Nielsen M A,Chuang I L.量子计算和量子信息(一)[M].北京:清华大学出版社,2006.

