灰色支持向量机在机场吞吐量预测中的应用
徐勤兰, 樊重俊, 张 鹏
(上海理工大学管理学院,上海 200093)
货邮吞吐量是机场吞吐量的重要组成部分,是 机场运营管理的重要依据之一,是实现机场资源有效配置的基本依据.随着我国航空业的迅速发展,机场货邮吞吐量也增长迅猛,为实现机场及航空公司的有效管理,提高货邮吞吐量的预测精度越来越成为人们关注的重点.传统的预测方法按性质大致可分为两类[1-2]:定性预测法和定量预测法.定性预测法注重事物发展性质方面的预测,具体方法主要有德尔菲法、主观概率法、专家会议法,这些方法有较大的灵活性、操作简单、可靠性好,但受主观因素影响较大.定量预测法关注事物在数量上的变化,主要包括时间序列法、趋势外推法、计量经济法、重力模型法、灰色预测法、神经网络法等,但神经网络预测法具有较强的经验色彩,受网络结构复杂度和样本复杂度的影响较大,会出现泛化能力差和过学习等现象.这些传统的预测方法通常在处理线性数据时有较好的应用,但在处理非线性数据时常常不能满足人们的要求.随着人们对数据处理的精度要求越来越高,而单一的预测模型必然存在某方面的盲区,因此,利用组合预测模型进行数据处理,优势互补,提高预测精度,成为一种研究的趋势.本文重点关注灰色系统与支持向量回归机组合模型的研究以及在机场货邮吞吐量预测中的应用.
灰色系统理论是我国著名学者邓聚龙于1982年创立的一门学科,以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定系统为研究对象.GM(1,1)模型是灰色系统理论的重要组成部分,具有建模所需数据少的特点[3].支持向量机(support vector machines,SVM)是Vapnik等在统计学习理论(statistical learning theory,SLT)的基础之上提出的一种新的机器学习方法[4].它基于结构风险最小化原则来提高泛化能力,有效解决了小样本、非线性、高维数、局部极小点等实际问题,具有良好的推广性和较好的分类精确性.
将灰色系统与支持向量机组合起来得到灰色支持向量机模型,此模型既具有灰色系统在处理“小样本”、“贫信息”数据方面的优势,又具有支持向量机在处理不规则、混沌等非线性数据方面的自适应能力.
1 灰色预测模型[3]
灰色预测的实质是将“随机过程”当作“灰色过程”,“随机量”当作“灰色量”,并以灰色系统理论中的GM(1,1)模型为主进行数据分析处理.GM(1,1)模型的主要建模过程如下:
令非负原始序列为x(0),对x(0)作一次累加生成得到1-AGO序列,即
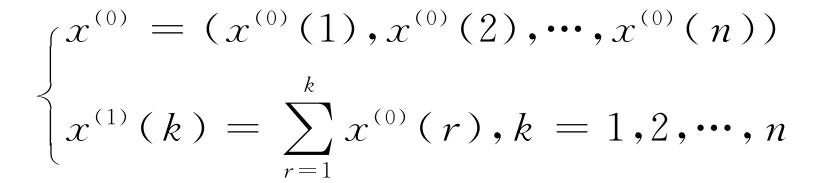
则x(0),x(1)符合灰导数条件,将x(0),x(1)各时刻数据代入灰色微分方程
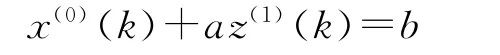
其中
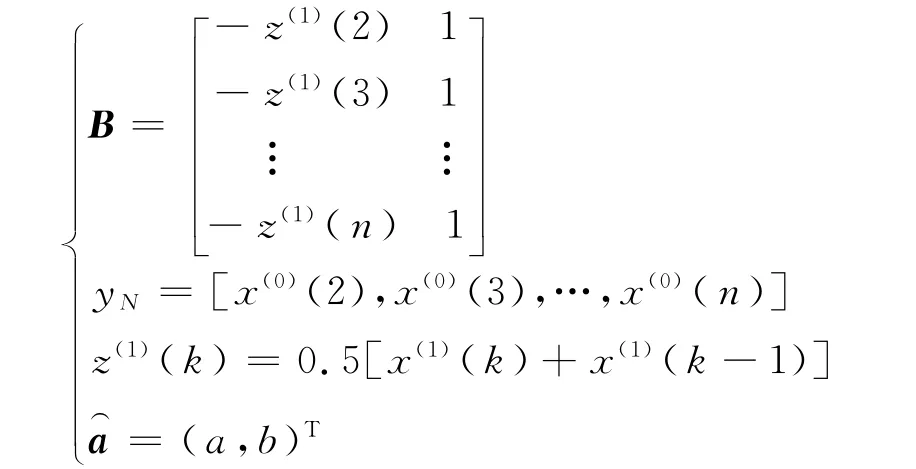
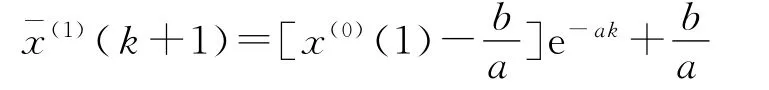
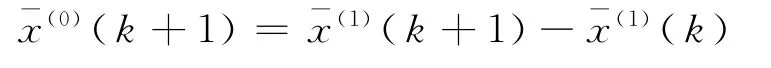
2 支持向量机模型[5-8]
支持向量机模型已在模式识别、回归分析、文章分类等领域得到了应用,并取得了较好的效果,其基本思想如下:
这时非线性回归问题的优化方程转化为
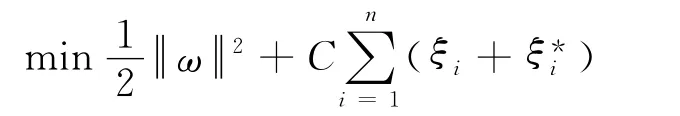
其中,ξi,ξ*i≥0,i=1,2,…,n,且约束于
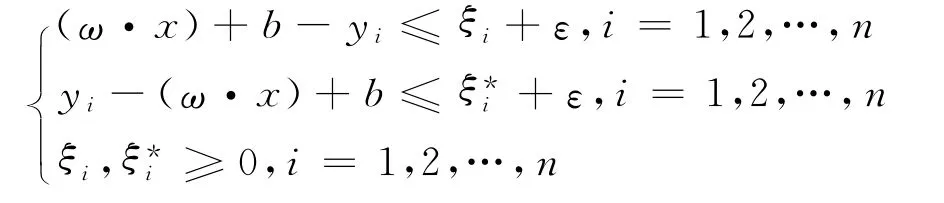
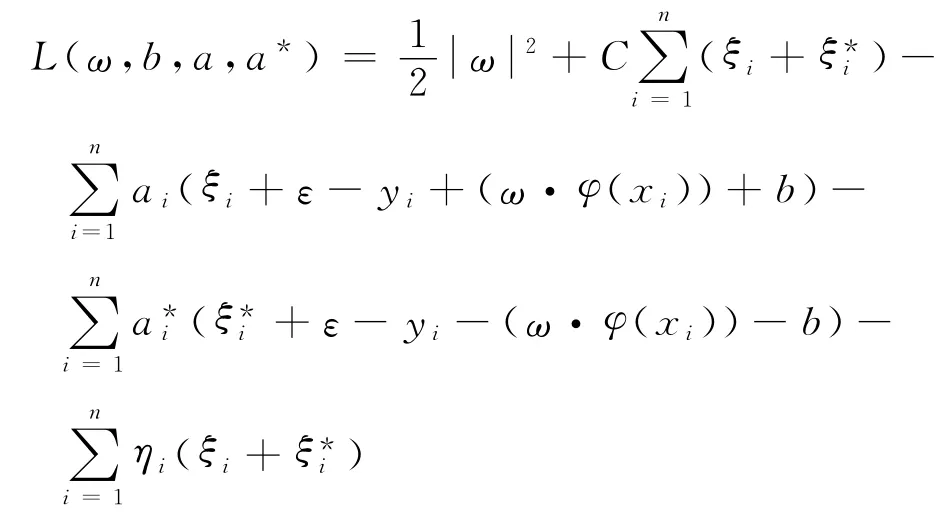
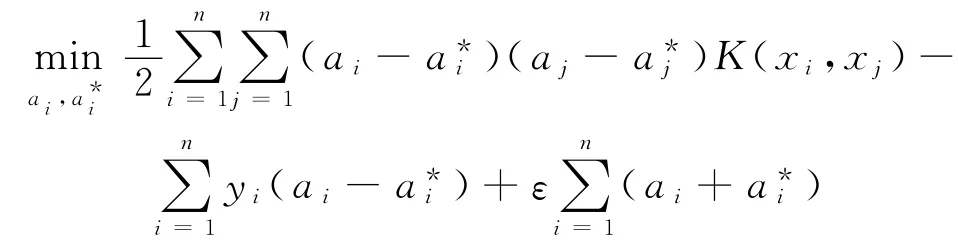
约束于
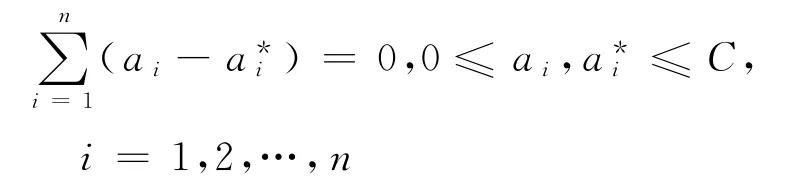
求解此对偶问题,可得到回归决策函数为
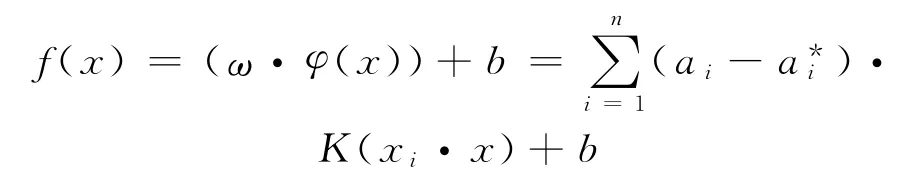
3 灰色支持向量机建模过程
机场货邮吞吐量的产生受多种因素的影响,而许多影响因素在做数据预测时不易定量处理或有些因素尚不明确,因此本文尝试结合灰色模型与支持向量机模型各自的优点,建立灰色支持向量机模型,基本思想如下:
a.设原始序列为
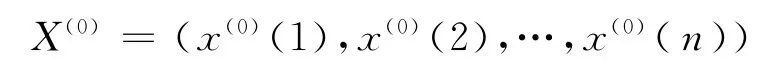
其中,x(0)(k)≥0,k=1,2,…,n,利用上述G(1,1)模型对原始序列进行分析预测,得到预测值
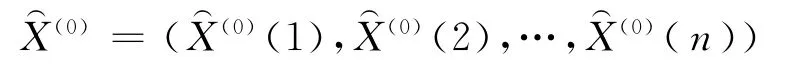
b.设原始序列值X(0)(k)与G(1,1)模型预测值X⌒(0)(k)的比值为d(0)(k),k=1,2,…,n.从比值序列中选取模型的训练样本集和测试样本集.
c.选择适当的核函数K(xi,x)及参数.
d.用支持向量机方法求解比值序列优化问题的Lagrange对偶问题,并构造回归决策函数f(x).
e.利用回归决策函数f(x),计算出比值序列d(0)(k)的预测值
4 实证研究
以上海浦东机场和上海虹桥机场2009年9月~2010年12月货邮吞吐量数据为研究对象,数据见表1.
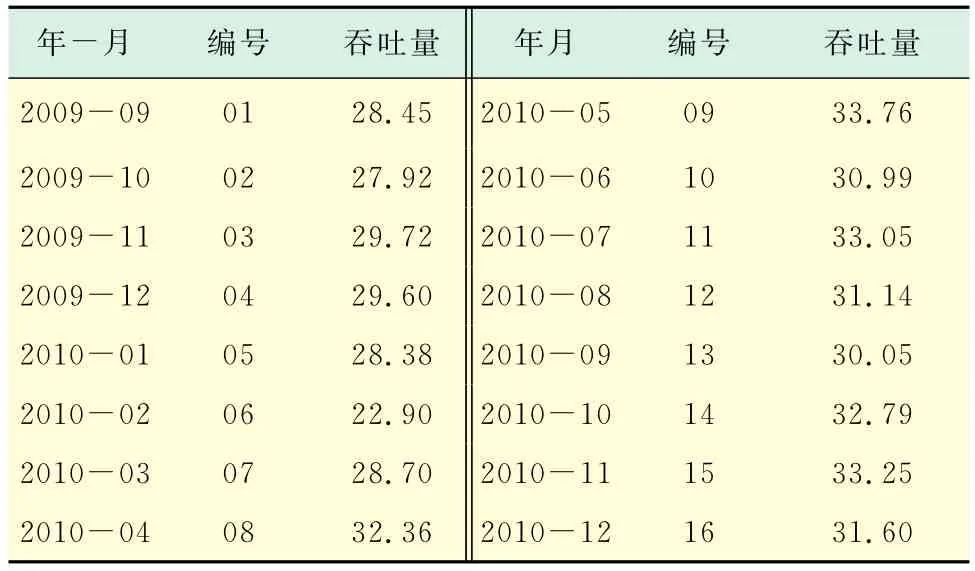
表1 2009年9月~2010年12月年上海机场货邮吞吐量Tab.1 Cargo and mail throughput of the Shanghai airport in 2009.9~2010.12 万t
首先,利用表中01~12的数据建立灰色G(1,1)模型,并利用此模型对2010年9月~2010年12月的吞吐量进行分析预测,其预测结果及误差见表2.
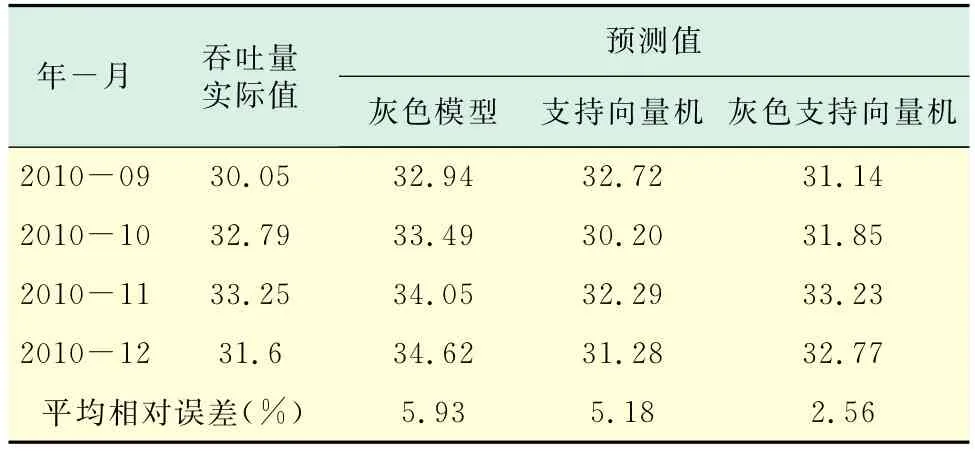
表2 模型预测值及误差Tab.2 Predictive value and error of the model万t
其次,利用支持向量机与灰色支持向量机理论建立分析预测模型,其间需要做如下工作:
a.选取训练样本与测试样本 支持向量机选取原始数据中01~12的数据作为训练样本,13~16的数据作为测试样本.灰色支持向量机选取比值序列中01~12的数据作为训练样本,并利用均值生成法处理编号为06的异常数据,13~16的数据作为测试样本.
b.选择核函数 由于径向机基函数具有较好的普适性,且在处理时间序列问题时表现一般比其它核函数更好,因此,选用径向基函数K(xi,xj)=作为灰色支持向量机模型与支持向量机模型的核函数.
c.选择最优参数 需要确定的参数有不敏感损失误差ε、惩罚系数C以及核函数参数σ.然而,对这3个参数的选择,目前尚没有较好的方法,也没有较成熟地选取理论与指导原则[9],其主要的选择算法有留一法、交叉验证法、试凑法、网格搜索法、梯度下降法和免疫算法等.本文选取计算精度较高的交叉验证法作为参数的选择算法,其基本原理为:将训练数据集分成k份相等的子集,每次将其中k-1份数据作为训练数据,而将另外一份数据作为测试数据.这样重复k次,根据k次迭代后得到的均方误差平均值来估计期望泛化误差,最后选择一组最优的参数[10].
经计算得支持向量机的最优参数为C=4.0、σ=8.0、ε=0.001;灰色支持向量机的最优参数为C=256.0、σ=0.001、ε=0.001.
最后,分别利用支持向量机与灰色支持向量机对数据进行分析预测,预测及对比结果分别见表2和图1.
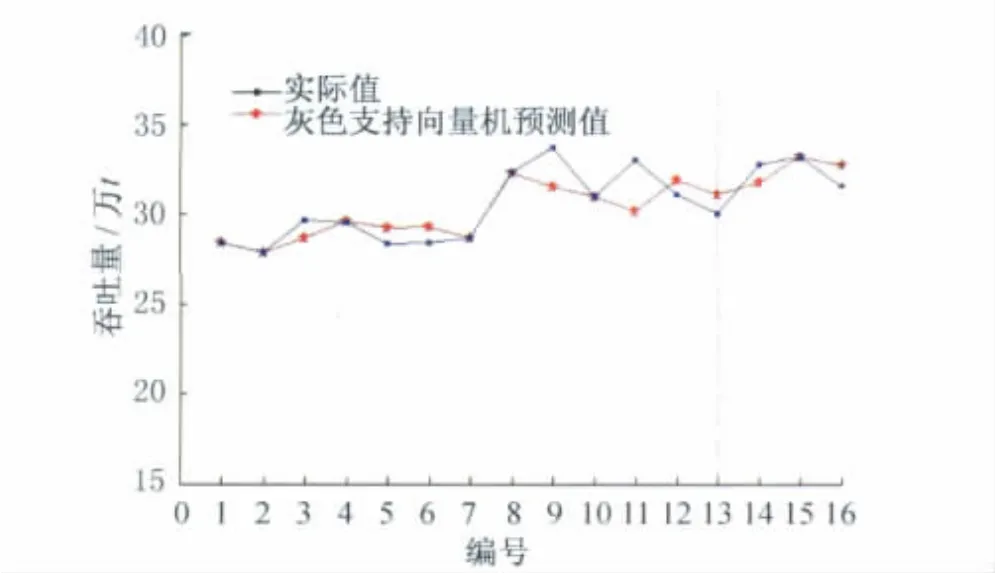
图1 灰色支持向量机分析结果与实际值的比较Fig.1 Compare gray support vector machine prediction results with the actual value
5 结束语
从结果及误差可以看出灰色支持向量机模型在分析预测机场货邮吞吐量方面明显优于灰色及支持向量机模型.灰色模型与支持向量机模型的融合弥补了单一模型在数据处理方面的缺陷,尽管组合模型中有个别数据拟合误差偏大,但从整体预测效果看,仍然优于单一的灰色模型或支持向量机模型.
由于机场货邮吞吐量的产生受多种因素影响,包括宏微观经济发展、贸易发展、资源状况等因素等,因此,预测机场货邮吞吐量时,不应仅仅考虑时间因素,也应综合考虑社会经济等综合因素,以建立更准确地预测模型,这也是以后要进一步深入研究的方向.
[1] 王芳.基于支持向量机的航段运量预测研究[D].江苏:南京航空航天大学,2007.
[2] 张慧,王喆.机场吞吐量预测方法探讨[J].中国民用航空,2008,10(94):67-68.
[3] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[4] Vapnik V.The nature of statistical learning theory[M].New York:Springer,1999.
[5] 董雁萍.支持向量机预测模型的构建及其应用[D].西安:西安理工大学,2010.
[6] 梁路宏,艾海舟,张钹.基于模板匹配与支持向量机的人脸检测[J].计算机学报.2002,25(1):22-29.
[7] Thissen U,Brakel R,Weijer A P,et al.Using support vector machines for tiem series prediction[J].Chemometrics and Intelligent Laboratory System,2003,69(1):35-49.
[8] Gavrishchaka V V,Ganguli S B.Volatility forecasting from multiscale and high-dimensional market data[J].Neurocomputing,2003,55(1):285-305.
[9] 朱家元,张喜斌.多参数装备费用的支持向量机预测[J].系统工程与电子技术,2003,25(6):701-703.
[10] 奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用,2011,47(3):123-128.

