单层倒悬链型柱面网壳的非线性稳定性研究＊

贺拥军，刘 旦，周绪红，2

（1.湖南大学土木工程学院，湖南长沙 410082； 2.兰州大学，甘肃兰州 730000）

柱面网壳因其构造简单、受力合理、体形美观、经济效果良好而得到广泛应用.相对于双层柱面网壳而言，单层柱面网壳在用钢量方面较前者节约较多，但由于其刚度较小，稳定问题显得尤为突出.近30年来，国内外学者在单层柱面网壳的稳定性研究方面取得了丰硕成果［1－6］，但是这些研究都是针对圆柱面网壳的（此类柱面网壳以圆弧拱为准线），而对其他拱准线形式的单层柱面网壳研究甚少，并且上述文献均以15m跨度圆柱面网壳作为研究对象，早已不能满足现代网壳建设的跨度要求，因此研究更大跨度下其他合理拱准线形式的柱面网壳显得十分必要.悬链线拱因在恒载作用下，拱截面只承受轴力而无弯矩，截面应力均匀，故能充分利用钢材料的抗压性能.依据悬链线拱的这种独特受力性能，选用悬链线拱作为柱面网壳的横向准线，便形成了一种新的柱面网壳结构——倒悬链型柱面网壳.本文针对24m跨度单层倒悬链型柱面网壳结构，首先对比分析了其常见的几种网格形式的稳定性能，初步确定了一种较合理的网格布置形式；然后进一步与单层圆柱面网壳进行了整体稳定性对比分析；最后从大规模参数分析入手，较全面系统地研究了单层倒悬链型柱面网壳的静力稳定性，包括长宽比、矢宽比、杆件截面尺寸、初始几何缺陷、荷载不对称分布等对极限荷载的影响，以期为该结构形式的应用提供理论指导和参考依据.

1 计算模型及分析方案

结构计算模型采用单层倒悬链型柱面网壳，单层倒悬链型柱面网壳即由倒置的悬链曲线作为柱面网壳的拱准线.考虑两端支承点等高单索的自重作用，可推导出等截面单索在自重作用下的几何形状曲线（即悬链线），其几何曲线方程如下：式中：f为单索中点垂度；l为单索跨度；C为常数，如图1（a）所示.

图1 单层倒悬链型柱面网壳常见类型Fig.1 Common categories of inverted catenary single－layer cylindrical reticulated shells

根据柱面网壳网格形式类型，本文单层倒悬链型柱面网壳选用如下3种常用的网格形式：矩形网格单向斜杆Ⅰ型、矩形网格单向斜杆Ⅱ型以及三向网格，如图1（b）所示.

本文利用通用有限元软件ANSYS，仅考虑结构几何非线性的影响，进行网壳结构承载力的全过程跟踪分析.分析中结构杆件均采用BEAM189梁元，网壳节点假定为刚接.

结构模型两纵边三向铰支，两端部设加劲立体拱形桁架.网壳波宽B均取24m；矢宽比f／B＝0.40，0.35，0.30，0.25，0.20；长宽比L／B＝1.0，1.5，2.0，2.5，3.0.在初始几何缺陷分析中，将网壳最低阶特征屈曲模态作为最不利初始几何缺陷分布模式，考虑初始缺陷值分别为r＝L／1 200，L／600和L／300三种情况，对于部分算例分析了更多不同大小缺陷对极限荷载的影响.活载p可能满跨均布或半跨均布，共考虑了活载p与均布恒载g的4种比例：p／g＝0，1／4，1／2，1.0.网壳杆件均采用圆钢管，截面尺寸选用Ф108×4.5.

2 网壳整体稳定性能对比分析

本节对单层倒悬链型柱面网壳和单层圆柱面网壳进行全过程跟踪分析，得到各自的荷载位移全过程曲线，对比分析结构刚度及承载力提高情况.

2.1 不同网格形式单层倒悬链型柱面网壳稳定性对比分析

取结构长宽比为2.0，矢宽比分别为0.40，0.35，0.30，0.25，0.20，对上述3种常见网格形式的单层倒悬链型柱面网壳进行极限分析，得到相应的极限荷载见表1，同时还给出了矢宽比为0.30时的荷载位移全过程曲线，如图2所示.

表1 不同网格形式倒悬链型柱面网壳极限分析结果Tab.1 Calculation results of the inverted catenary cylindrical reticulated shells with different grid configurations kN

由表1可以发现，相同矢宽比下，单层倒悬链型柱面网壳斜杆Ⅱ型与三向网格型的极限荷载相差不大，前者仅比后者略小；斜杆Ⅰ型的极限荷载在矢宽比较大（f／B≥0.3）时较前两者都要大，且相比提高有10%左右，而当矢宽比较小时，3种网格形式的单层倒悬链型柱面网壳极限荷载均十分接近.

图2 3种常见网格形式倒悬链型柱面网壳荷载位移全过程曲线对比Fig.2 Comparison of complete load－deflection curve between the three common grid configurations of inverted catenary cylindrical reticulated shells

由图2所示荷载位移全过程曲线可以看出，单层倒悬链型柱面网壳斜杆Ⅰ型的刚度相比斜杆Ⅱ型和三向网格型的刚度虽然稍低一些，但斜杆Ⅰ型网壳却表现出了更好的延性，按照规程（JGJ 61－2003）［7］规定，网壳结构位移值达到最大限制值B／400时，斜杆Ⅱ型和三向网格型单层倒悬链型柱面网壳已发生脆性失稳破坏，而斜杆I型单层倒悬链型柱面网壳却仍保持着良好的整体稳定性与延性.

由上可知，斜杆I型单层倒悬链型柱面网壳相比斜杆Ⅱ型和三向网格型单层倒悬链型柱面网壳具有更好的极限承载能力以及整体稳定性能.

2.2 单层倒悬链型柱面网壳与圆柱面网壳稳定性对比分析

同样取结构长宽比为2.0，矢宽比分别为0.40，0.35，0.30，0.25，0.20，对斜杆Ⅰ型单层倒悬链型柱面网壳、斜杆Ⅰ型圆柱面网壳以及三向网格圆柱面网壳进行极限分析，得到相应的极限荷载（见表2），图3给出了矢宽比为0.30时3种网壳的荷载位移全过程曲线.

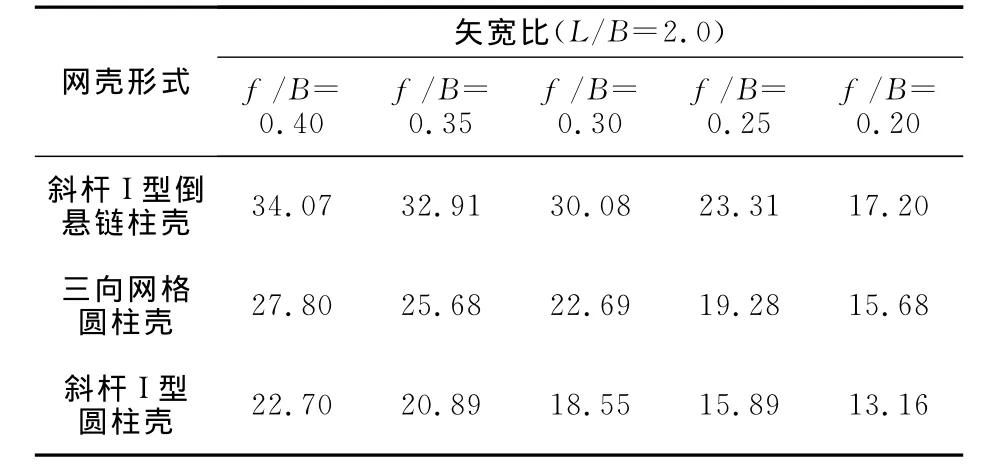
表2 倒悬链型柱面网壳与圆柱面网壳极限分析结果Tab.2 Calculation results of the inverted catenary cylindrical reticulated shells and cylindrical reticulated shells kN

由表2可以发现，三向网格圆柱面网壳的极限荷载要高于斜杆Ⅰ型圆柱面网壳，而斜杆Ⅰ型单层倒悬链型柱面网壳的极限荷载较斜杆Ⅰ型和三向网格圆柱面网壳都有较大提高，其提高率在矢宽比为0.30时取得最大，且分别最大提高了62%和32%.

图3 倒悬链型柱面网壳与圆柱面网壳荷载位移全过程曲线对比Fig.3 Comparison of complete load－deflection curve between inverted catenary cylindrical reticulated shells and cylindrical reticulated shells

由图3可以看出，在相同的极限荷载时，斜杆Ⅰ型圆柱面网壳的位移比三向网格圆柱面网壳大，而三向网格圆柱面网壳的位移又要比斜杆Ⅰ型单层倒悬链型柱面网壳的大.可见，单层倒悬链型柱面网壳整体刚度相比单层圆柱面网壳均有较大提高，而对于单层圆柱面网壳，三向网格圆柱面网壳又要比斜杆Ⅰ型圆柱面网壳刚度大，与文献［8］结论一致.

综合前面的分析可知，3种常见网格形式的单层倒悬链型柱面网壳，以斜杆Ⅰ型的整体稳定性能最好，且相比单层圆柱面网壳，斜杆Ⅰ型单层倒悬链型柱面网壳的刚度以及极限承载能力都得到了较大的提高.因此下文将以斜杆Ⅰ型单层倒悬链型柱面网壳为例，研究不同条件下结构的失稳模态及极限荷载，并就极限荷载进行了一系列的参数分析.

3 屈曲模态

大量计算分析表明，单层倒悬链型柱面网壳达到极限荷载发生失稳时，可能会出现如下一些屈曲模态，如图4所示.

图4 屈曲模态Fig.4 Bucking modes

1）网壳中部形成大面积凹陷，两侧被挤压而向外隆起，截面呈3个半波凹陷形式，如图4（a）所示；

2）网壳两侧中间向内凹陷，两侧底部被挤压而向外凸起，截面呈两边对称的变形形式，如图4（b）所示.

上述两种屈曲模态中，以第一种失稳模态最为常见，结构绝大多数情况下呈现出这种形式的屈曲；网壳结构仅在矢宽比大于0.2且长宽比为1.0的情况下，因周边对壳面具有很强的约束作用，才发生第二种形式的失稳.分析同时发现当荷载不对称分布时，网壳的屈曲模态仅向活荷载布置一侧略移，如图4（c）所示.

由上可见，单层倒悬链型柱面网壳的失稳一般首先发生在结构中部区域，网壳中部成为结构失稳的薄弱环节.经分析可发现，若在网壳中部增设横向立体加劲肋予以加强，则网壳整体稳定性能将得到较大提高，此时结构失稳模态如图4（d）所示.

4 几何参数分析

4.1 矢宽比及长宽比对极限荷载的影响

本节主要分析随矢宽比、长宽比的改变，宽度为24m的单层倒悬链型柱面网壳极限荷载的变化规律，图5为分析所得结构极限荷载与矢宽比及长宽比的关系曲线.

图5 极限荷载与长宽比及矢宽比关系Fig.5 Relationship between ultimate loads and length－span ratios and raise－span ratios

由图5可以看出，长宽比、矢宽比对网壳极限承载力的影响具有良好的规律性：相同矢宽比下，结构极限荷载随长宽比的增大而迅速减小；相同长宽比下，结构极限荷载随矢宽的增大而增大.同时可以发现，长宽比、矢宽比对单层倒悬链型柱面网壳极限承载力都具有较大影响，且相对矢宽比的影响，长宽比的影响更为显著.在实际工程设计中，对长宽比较大的单层柱面网壳，为改善其稳定性能，常沿长度方向加肋.由图5易知单层倒悬链型柱面网壳在长宽比超过1.0后结构极限承载能力急速下降，因此建议沿单层倒悬链型柱壳长度方向肋与肋的间距或肋与柱壳两端的距离应小于1倍网壳横向宽度.进一步分析发现，较大长宽比的网壳沿长度方向按上述原则（取肋间距为1倍网壳横向宽度）加肋以后，结构极限承载力的确得到了较大提高，其极限荷载仅稍低于长宽比为1.0的网壳.

4.2 杆件截面尺寸对极限荷载的影响

取结构矢宽比为0.3，分别取杆件截面为Ф89×4，Ф108×4.5，Ф127×4.5，Ф140×4.5进行分析，得到结构极限荷载随杆件截面的变化关系如图6所示.图6中以等代刚度作为关系曲线的横坐标来表示网壳杆件截面的大小，其中B和D分别为等代薄膜刚度和等效抗弯刚度，B和D的具体计算方法见文献［7］.

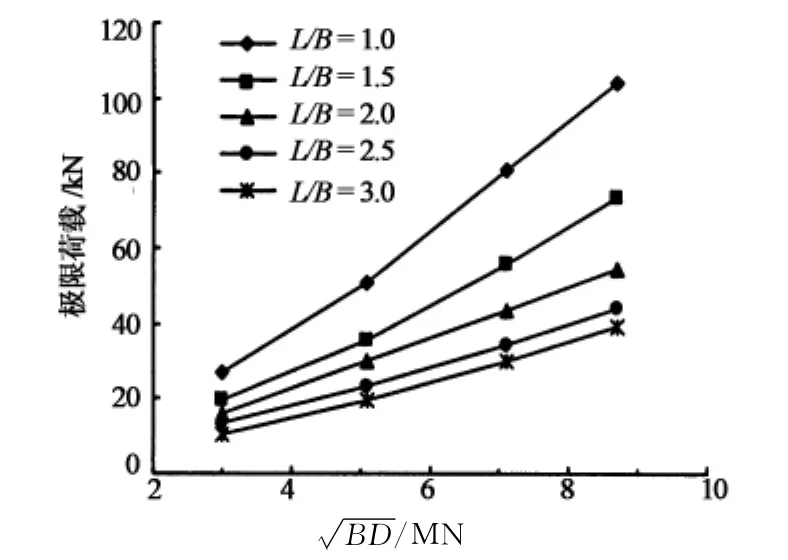
图6 结构极限荷载与杆件截面关系Fig.6 Relationship between ultimate loads and cross－section of the elements

由图6可以看出，随着杆件截面的增大，刚度的提高，网壳极限承载力随截面刚度的变化更具有规律性，大致呈线性增长关系.

5 初始几何缺陷对极限荷载的影响

初始几何缺陷的存在往往会使结构屈曲模态发生改变，进而导致网壳极限承载能力的降低.针对这一影响，本文对每一例网壳均进行了初始缺陷（r＝L／1 200，L／600，L／300）影响分析.

分析结果统计显示（由于篇幅限制，此处不列出具体数据），当初始缺陷为L／1 200时，网壳极限荷载降低率平均值为16%，最高达27%；初始缺陷为L／600时，平均值为27%，最高可达52%；初始缺陷为L／300时，平均值为34%，最高可达57%.由此可见初始几何缺陷对单层倒悬链型柱面网壳极限承载力的影响比较显著.同时还应当指出，当引入缺陷进行极限分析时，网壳屈曲模态与其相应的特征值最低阶屈曲模态相一致.

为进一步研究缺陷对结构极限承载力的影响规律，选取矢宽比为0.25，长宽比为2.0的单层倒悬链型柱面网壳，分别考虑7种大小不同的初始几何缺陷（r＝0，2，4，6，8，10，12cm）进行分析，图7为网壳极限荷载随缺陷值变化的曲线.

图7 不同缺陷时的全过程曲线及极限荷载变化曲线Fig.7 Complete load－deflection curve and ultimate load curve of shells with different initial imperfections

由图7可以看出，在开始缺陷值较小（r≤L／300）时，网壳极限荷载随缺陷增大急速下降.当缺陷值超过L／300（r＝8cm）后，极限荷载随缺陷增大变幅不大，曲线趋于平缓，按照规程（JGJ 61－2003）［7］规定选取L／300作为圆柱面网壳极限荷载计算的初始缺陷值，对于单层倒悬链型柱面网壳来说，同样也是合理的.

6 荷载不对称分布对极限荷载的影响

对每例单层倒悬链型柱面网壳按4种竖向荷载比例（p／g＝0，1／4，1／2，1.0）的不对称布置进行极限分析，并以p＋g来定义极限荷载.为节约篇幅，图8仅给出了矢宽比为0.30时单层倒悬链型柱面网壳完善结构以及非完善缺陷（r＝L／600）结构极限荷载随不同比例不对称荷载的变化曲线.活荷载／恒荷载（p／g）（a）f／B＝0.30，r＝0活荷载／恒荷载（p／g）（b）f／B＝0.30，r＝4cm

图8 极限荷载随不同比例不对称荷载变化曲线Fig.8 Curves of ultimate loads under unsymmetrical distribution of loads

由图8可知，完善结构的极限承载能力因荷载不对称而降低，但降低的幅度并不大，分析结果统计显示，完善结构极限荷载最大仅降低28%.对于存在初始缺陷的不完善网壳，结构的极限承载能力并没有因荷载不对称而降低，反而有所上升，可见结构存在初始缺陷时，荷载不对称分布对网壳极限荷载并没有表现出耦合降低作用，而是起到了有利作用.

综上可知，在竖向不对称荷载作用下，结构极限荷载变化幅度并不大，单层倒悬链型柱面网壳对不对称荷载作用并不敏感.

7 结 论

本文主要得出以下结论：

1）单层倒悬链型柱面网壳常见3种网格形式中，以斜杆Ⅰ型的整体稳定性能最好，且相比单层圆柱面网壳，斜杆Ⅰ型单层倒悬链型柱面网壳的刚度及极限承载能力也都得到了较大的提高.

2）长宽比和矢宽比对单层倒悬链型柱面网壳稳定性能都存在显著影响并具有良好的规律性，且相对矢宽比、长宽比对网壳的影响更为明显.同时建议用以提高网壳稳定性能的横向立体加劲肋间距应小于1倍网壳横向宽度.

3）截面等效刚度对单层倒悬链型柱面网壳极限荷载的影响几乎呈线性关系.

4）初始缺陷对于单层倒悬链型柱面网壳极限承载力影响比较显著，按初始缺陷为L／300考虑，网壳极限荷载降低率平均值为34%，最高可达57%.

5）结构对竖向不对称荷载作用不敏感.

［1］ YAMADA S，TAKEUCHI A，TADA Y，et al.Imperfectionsensitive overall buckling of single－layer latticed domes［J］.Journal of Engineering Mechanics，2001，4：382－386.

［2］ KATO S，YAMAUCHI Y，UEKI T.Buckling load of elliptic paraboloidal single layer reticulated roofs under uniform load［J］.International Journal of Space Structures，2005，20（2）：91－106.

［3］ 沈世钊，陈昕，张峰，等.单层柱面网壳的稳定性［J］.空间结构，1998，4（2）：17－28；4（3）：53－55.SHEN Shi－zhao，CHEN Xin，ZHANG Feng，et al.Stability of single－layer lattice vaults［J］.Spatial Structures，1998，4（2）：17－28；4（3）：53－55.（In Chinese）

［4］ 张峰.单层柱面网壳非线性稳定性分析［D］.哈尔滨：哈尔滨建筑大学建筑与土木工程学院，1997.ZHANG Feng.Nonlinear stability analysis of single－layer cylindrical reticulated shells［D］.Harbin：Architecture University of Harbin，College of Architecture and Civil Engineering，1997.（In Chinese）

［5］ 陈军明，陈应波，李秀才.单层柱面网壳结构的非线性稳定性研究［J］.武汉理工大学学报，2003，25（4）：51－54.CHEN Jun－ming，CHEN Ying－bo，LI Xiu－cai.Study on nonlinear stability of single－layer cylindrical reticulated shells［J］.Journal of Wuhan University of Technology，2003，25（4）：51－54.（In Chinese）

［6］ 曹正罡，孙英，范峰，等.单层柱面网壳弹塑性稳定性能研究［J］.土木工程学报，2009，42（3）：55－59.CAO Zheng－gang，SUN Ying，FAN Feng，et al.Elasto－plastic stability of single－layer cylindrical reticulated shells［J］.China Civil Engineering Journal，2009，42（3）：55－59.（In Chinese）

［7］ JGJ61－2003网壳结构技术规程［S］.北京：中国建筑工业出版社，2003.JGJ61－2003Technical specification for latticed［S］.Beijing：China Architecture and Building Press，2003.（In Chinese）

［8］ 张文福，王秀丽，尹德钰.空间结构［M］.北京：科学出版社，2005：103－105.ZHANG Wen－fu，WANG Xiu－li，YIN De－yu.Spatial structures［M］.Beijing：Science Press，2005：103－105.（In Chinese）