长周期光纤光栅模式与耦合系数的研究＊

谢 中，冯双磊，周艳明，李 科，马扬昭

（湖南大学物理与微电子科学学院，湖南长沙 410082）

长周期光纤光栅（LPG）具有插入损耗小、带宽宽、后向反射低、制作简单、成本低而且比Bragg光栅的灵敏度更高等优点［1］，已广泛应用于通信、传感等领域.长周期光纤光栅的周期比光纤布拉格光栅的周期大得多，在几十到几百微米之间.这样的结构使前向传输的纤芯基模与同向传输的各阶次包层模之间发生耦合.在透射谱中，一些波长符合长周期光纤光栅相位匹配条件的模的强度大为减弱，就形成了一系列的损耗峰［2］.长周期光纤光栅包层模与纤芯模之间的耦合系数是影响损耗峰峰值的重要因素之一.关于耦合系数已有大量的研究，其中有文章［3－4］报道，包层模与纤芯模之间的耦合系数随波长增大而减小.随着全光网络的提出、光器件设计理论和制备工艺的发展、以及对器件工作性能和能量消耗等要求的提高，减小器件尺寸、提高集成度，将光子器件与微电子、光电子器件在纳米尺度上混合集成已成为必然趋势，这就要求光波导线宽度向亚波长和纳米尺寸发展.本文针对这一发展趋势，对半径较小的光纤长周期光栅的耦合系数进行了研究.运用耦合模理论和常用的3层光纤模型和Math－CAD计算得出了在不同光纤参数下包层模与纤芯模之间的耦合系数随波长变化的规律，对耦合系数随波长的变化进行了全面的数值分析.计算模拟的结果表明：与以前研究结果［3－4］不同，包层模与纤芯模之间的耦合系数随波长的增大而增大.当改变光纤其他参数时包层模与纤芯模之间的耦合系数随波长变化亦有不同的规律.这些结果可为今后长周期光纤光栅器件微型化设计提供参考.

1 长周期光纤光栅纤芯模和包层模有效折射的分析

1.1 纤芯基模特征方程

纤芯基模特征方程［5－6］如下：

式中：V＝（2π／λ）a1，为归一化频率；b＝（－）／（－），为归一化有效折射率；λ为光波波长；a1为光纤纤芯半径；n1和n2分别为光纤纤芯、包层的折射率；为纤芯基模的有效折射率；J0，J1和K0，K1分别为0阶、1阶第一类贝塞尔函数和0阶、1阶第二类虚宗量贝塞尔函数，解方程（1）可得出纤芯基模的有效折射率.

1.2 包层模的本征方程

包层模的本征方程如下：

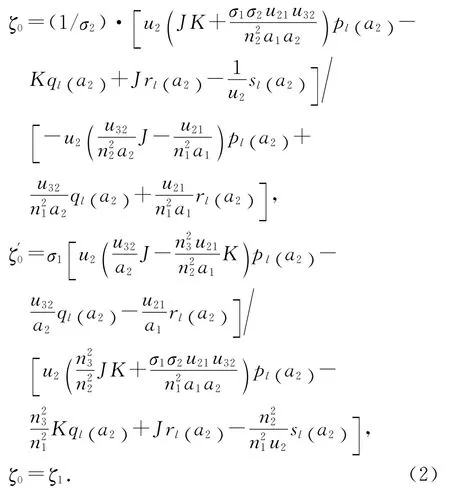
方程中的各参数参看文献［6－7］，解超越方程（2）可得出一阶各次包层模的有效折射率.

图1为一阶前20次包层模有效折射率随波长的变化曲线.计算采用的光纤参数：纤芯折射率n1＝1.458，包层折射率n2＝1.45，纤芯半径a1＝2.625μm，包层半径a2＝62.5μm，包层外折射率n3＝1.

图1 有效折射率随波长的变化Fig.1 The effective refractive index with wavelength

从图1中可知一阶各次包层模的有效折射率随波长的增加而减小，而且模次越大的模对应的有效折射率随波长减小得越快，另外奇次和奇次包层模、偶次和偶次包层模有效折射率的纵向间距随波长的增大而增大.

2 一阶各次包层模耦合系数的研究

本文用三层光纤模型和耦合模理论研究阶跃单模光纤中写入的均匀长周期光纤光栅的纤芯基模与一阶各次包层模之间的耦合.纤芯基模与一阶各次包层模耦合的耦合系数公式为［6］：

式中：σ（z）为纤芯平均折变量，对于均匀的长周期光纤光栅σ（z）为常数；表示总功率为1W所表征的一阶v次包层模式的归一化常量，可以通过解光纤归一化功率模型得出［8］：

式中：Pco，Pcl，Pex分别为某一包层模式在纤芯、包层、环境层中的功率；，表示磁场幅角方向、径向分量的复共轭；，表示电场幅角方向、径向分量，这些分量均与有关.求出的代入式（2）即可求得耦合系数的值.

2.1 波长对耦合系数随模次变化的影响

图2为在上述光纤参数下计算得出的不同波长时耦合系数随包层模模次的变化.

图2 不同波长下耦合系数随模次的变化Fig.2 The coupling coefficient of different wavelengths with mode number

从图2中可知，奇次包层模（HE模）的耦合系数远大于偶次包层模（EH模）的耦合系数，且偶次包层模耦合系数随模次的变化很小.各波长下奇次包层模的耦合系数随模次先增大后减小，随着波长的增大奇次模的耦合系数随模次增大得越来越慢，波长为1.52μm，1.60μm时耦合系数随模次先增大后减小，另外最大耦合系数对应的模次随波长的减小而增大.因为一阶低偶次模和一阶高次模的能量相对较小，所以下文分析长周期光栅的模式耦合时可只考虑纤芯基模与一阶低奇次包层模之间耦合，而忽略纤芯基模与其他次包层模（一阶低偶次包层模和一阶高次包层模）之间的耦合［9］.

2.2 光纤参数对耦合系数随波长变化的影响

影响长周期光纤光栅包层模耦合系数的光纤参数主要有纤芯和包层的半径a1和a2，纤芯和包层的折射率n1和n2，包层外介质的折射率n3（设n3＝1）.把以上光纤参数代入式（3），通过数值计算得出耦合系数随波长变化的情况，光纤初始结构参数取值同前.研究长周期光栅透射谱时一般只考虑前5个奇次包层模和纤芯基模的耦合，因此计算时只提取了模次v＝1，3，5，7，9次包层模的耦合系数，波长范围为1.2～2.0μm.图3（a）为初始结构参数下耦合系数随波长变化的曲线，由图可知，v＝1，3，5次包层模的耦合系数随波长的增大而增大；v＝3，5次模的耦合系数随波长而增大得越来越慢；v＝7，9次包层模的耦合系数则随波长的增大先增大后减小.

当纤芯折射率n1＝1.46，其他光纤参数为初始结构参数时，耦合系数随波长变化如图3（b）所示，由图中可知v＝1，3，5，7，9次包层模耦合系数随波长的增大而增大；v＝7，9次包层模的耦合系数随波长的增大变化得越来越慢，且各次模对应的耦合系数比图3（a）要小约0.05.

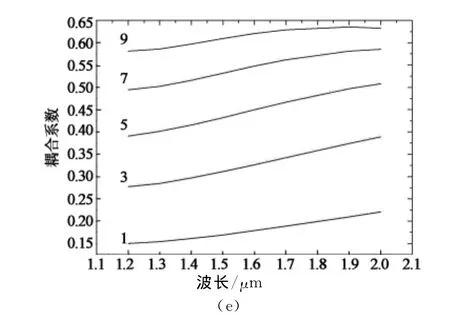
图3 不同光纤参数下耦合系数随波长的变化Fig.3 The coupling coefficient with wavelength in different optical fiber parameters

图3（c）显示了包层折射率n2＝1.453，其他光纤参数为初始结构参数时，包层模耦合系数随波长变化的关系，图中v＝1包层模的耦合系数随波长增大一直增大且增大得越来越慢；v＝3，5，7次包层模的耦合系数随波长增大先增大后减小，且增大比减小的慢；模次v＝9的耦合系数随波长的增大不断减小，且各次模的耦合系数比图3（a）中的大约0.1

图3（d）为纤芯半径a1＝4.15，其他光纤参数为初始结构参数时，耦合系数随波长变化的规律.图中各次包层模的耦合系数随波长的增大先减小后增大，这与上述3种情况下各次包层模耦合系数随波长变化的规律恰好相反，而且耦合系数随波长减小比增大的快.

图3（e）为用文献［3］中光纤参数计算得出的包层模耦合系数随波长变化曲线.图中v＝1，3，5，7，9次包层模的耦合系数随波长增大而增大，这与文献［3］中v＝1，3，5，7，9次包层模的耦合系数（即交流耦合系数）随波长增大而减小的研究结果不同，原因是文献［3］应用的耦合系数的计算公式［10］与本文应用的耦合系数的计算公式［3］不同.经软件模拟仿真与运用公式计算结果进行对比，作者发现运用文献［6］中公式计算所得的长周期光纤光栅包层模耦合系数更为合理.

2.3 耦合系数对光栅透射谱的影响

设光栅长度均为2cm，折射率调制均为0.000 2，依照图3中各光纤参数，运用OptiGrating4.2模拟的光栅透射谱如图4所示，图4（a），（b），（c），（d），（e）.分别对应图3（a），（b），（c），（d），（e）.对长周期光栅透射谱而言，包层模耦合系数越大，损耗峰波长在该模次的透射率就越小，即损耗峰峰值就越大.从图4（a）中很明显看出7次模对应的损耗波长的透射率最小，这是因为图3（a）中7次模对应的损耗波长的耦合系数比其他模次对应的损耗波长的耦合系数都大，图3（c）中3次模在波长为1.5μm处的耦合系数比1次模和5次模在波长分别为1.3μm和1.95μm处的耦合系数都大.

图4 不同光纤参数下均匀长周期光纤光栅透射谱Fig.4 The transmission spectrum of LPG in different optical fiber parameters

由以上计算模拟结果可知光纤参数对耦合系数随波长变化的规律有很大影响，耦合系数的大小又直接影响到光栅透射谱损耗峰的峰值，因此选取合适的光纤参数对长周期光纤光栅的设计至关重要.

3 结 论

本文着重研究了小芯径长周期光纤光栅的一阶低奇次包层模的耦合特性.基于耦合模理论，对一阶低奇次包层模有效折射率、耦合系数及光栅的透射谱进行了计算模拟.结果表明，不同波长下包层模最大耦合系数对应的模次随波长的增大而减小，包层模与纤芯模之间的耦合系数随波长的增大而增大.当改变光纤其他参数时，包层模与纤芯模之间的耦合系数随波长变化亦有不同的规律.这些结果对进一步研究长周期光纤光栅的透射谱特性及今后长周期光纤光栅器件微型化设计有重要参考价值.

［1］ JAMES S W，TATAN R P.Optical fiber long－period grating sensors：characteristics and application［J］.Meas Sci Technol，2003，14：R49－R61.

［2］ 张自嘉.光纤光栅理论基础与传感技术［M］.北京：科学出版社，2009：138.ZHANG Zi－jia.Long optical fiber grating theoretical basis and sensor technology［M］.Beijing：Science Press，2009：138.（In Chinese）

［3］ 崔春雷，刘伟平，黄红斌，等.长周期光纤光栅包层模特性及其对传输谱的影响［J］.光子学报，2005，34（10）：1569－1572.CUI Chun－lei，LIU Wei－ping，HUANG Hong－bin，et al.Cladding modes characteristic and its effects on transmission spectrum of long period fiber gratings［J］.Acta Photonica Sinica，2005，34（10）：1569－1572.（In Chinese）

［4］ 黄桂岭，赵启大，刘松，等.长周期光纤光栅透射谱与结构参数关系的研究［J］.光电子·激光，2007，18（5）：519－522.HUANG Gui－ling，ZHAO Qi－da，LIU Song，et al.Study of the relation between the transmission spectra and the structural parameters for a long－period fiber grating［J］.Journal of Optoelectronics，Laser，2007，18（5）：519－522.（In Chinese）

［5］ GLOGE D.Weakly guiding fibers［J］.Appl Opt，1971，10：2252－2258.

［6］ ERDOGAN T.Cladding－mode resonances in short and longperiod fiber grating filters［J］.J Opt Soc Am A，1997，14（8）：1760－1773.

［7］ ERDOGAN T.Cladding－mode resonances in short and long－period ber grating fiters：errata［J］.J Opt Soc Am A，2000，17（11）：2113.

［8］ PERAL E，CAPMANY J.Generalized bloch wave analysis for fiber and waveguide grating［J］.Light－wave Technology，1997，15（8）：1295－1302.

［9］ 饶云江，王义平，朱涛，等.光纤光栅原理及应用［M］.北京：科学出版社，2006：260－266.RAO Yun－jiang，WANG Yi－ping，ZHU Tao，et al.Long period fiber grating principle and application［M］.Beijing：Science Press，2006：260－266.

［10］何万迅，施文康，叶爱伦，等.长周期光纤光栅模式与耦合的研究［J］.光子学报，2003，23（3）：302－306.HE Wan－xun，SHI Wen－kang，YE Ai－lun，et al.Modes and couplings of long period fiber grating［J］.Acta Optica Sinica，2003，23（3）：302－303.（In Chinese）