瑞利索莫菲衍射与物理光学积分的应用比较

梁 彬 白 明 金 铭 苗俊刚

(北京航空航天大学电子信息工程学院，北京 100191)

近年来，随着微波技术的发展，无线电系统的工作频率逐渐升高，使得传统基于无线电波理论体系和光学理论体系之间的界限逐渐模糊.特别在处理毫米波、亚毫米波的各种电磁场问题时，人们开始尝试利用光学领域中的理论和方法来解决，并出现了准光学［1－4］等交叉学科以适应新要求的分析方法体系.

相干电磁场传播的衍射计算一直以来在不同的领域有着不同的理论和处理方法.除了波长或频率的巨大差别，光学领域与无线电领域分别采用不同的衍射积分公式处理具有相同物理过程的电磁波衍射问题.在光学理论体系中，瑞利索莫菲(RS，Rayleigh-Somerfield)标量衍射理论是处理光场传播的基本理论［5－6］.而在电磁波的相对低频波段，即无线电波频段，计算电磁场的传播问题时，采用的则是出发点不同的物理光学计算方法［7－11］.需要说明的是，这里的物理光学，不是对光学的描述，而是经典的无线电波领域处理衍射的矢量积分方法.

尽管上述两种电磁场计算方法各自已经非常成熟，针对准光学电磁计算技术的发展的需要，本文对光学RS标量衍射积分和物理光学积分方法进行了对比和分析.首先讨论二者依据不同出发点得到的最终积分公式在形式上的一致性与区别，然后结合数值仿真的算例，讨论RS积分公式在处理高频微波波段电磁场传播中的应用.

1 物理基础

1.1 RS标量衍射积分

RS标量衍射积分是光波频段经典的衍射计算方法，是被广泛采用的计算和分析光学传播的基本方法，其典型应用是计算薄屏遮挡后光的衍射场.RS衍射积分公式的基础是单色波标量场满足亥姆霍兹(Helmholtz)方程［12］，在推导过程中，构建特定的空间格林函数:

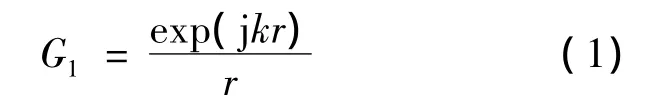
利用格林定理的数学关系得到最终的积分方程.与基尔霍夫衍射理论不同的是，RS衍射理论所选取的格林函数消除了基尔霍夫衍射理论中的不自洽性，但二者没有本质的区别，只在数学上有不同的处理方法.已经证明，两者只在衍射距离在波长量级上解才有差别［13］.总之，RS积分公式作为标量衍射积分理论，可以得到相当精确的衍射结果.

1.2 物理光学积分

物理光学积分方法源自斯特拉顿-朱兰成(SC，Stratton-Chu)积分方程［7］，是处理无线电波波段电磁散射问题的重要和经典的方法.SC方程也被称为场方程的直接积分，物理上是将电磁场的真实场源(电荷、电流和磁荷、磁流)与电场或磁场通过一个积分方程联系起来，可以通过求解积分方程得到电磁场的精确解.作为一种典型的高频近似算法，在散射体尺寸远大于波长时［9］，物理光学法用切向平面来近似积分中的等效源分布，从而通过积分公式求解电磁场的分布.在SC方程推导过程中，场源与电磁场之间通过位函数连接在一起，其中使用了空间格林函数:

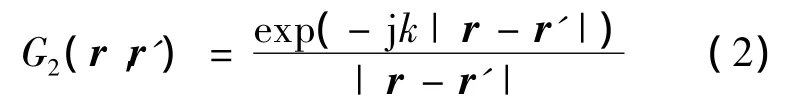
这一空间格林函数从而在交变场中将电流、磁流与磁矢位、电矢位联系了起来.

1.3 二者的比较

物理概念上，两种积分方法都源自格林函数，即通过积分求理想点源在各特定边界条件的传播解.而区别在于，二者采用了形式不同的格林函数，因此两种方法的数学形式有所不同.但是，其中最重要的区别在于物理光学法的辐射源是物理上实际存在的矢量电(磁)流源，而RS积分则以自由空间电磁波的场分布为次级波传播的波源.事实上自由空间的电磁波可以根据等效原理等效为电(磁)流源，因此在自由空间电磁波情况下，无线电波波段的物理光学积分法与RS衍射积分法从不同的出发点应该得到相同的电磁波计算公式.另一方面，物理光学积分比RS积分有着更一般的适用范围.不仅在矢量与标量的区别上，特别在当电场与磁场不满足空间波阻抗或等相位关系时，物理光学积分可以分别计算电场和磁场对波传播的贡献，然后再相干叠加，而RS积分方法对单一场分量进行计算将不能得到正确的结果.

2 数学形式

尽管二者在自由空间电磁波传播情况下的物理概念上有必然的统一，但具体公式形式上仍有需要注意的差别.本文以自由空间中电磁场的传播问题为例进行说明.考虑平行平面间的电磁场传播:由已知的平面场分布得到传播后其它位置处的平面场分布［14］，如图1所示.本文将利用RS积分公式和物理光学积分公式分别来进行处理该衍射问题，以作对比.

图1 平行平面场点位置关系示意图

首先采用RS衍射积分方法计算上述口面电磁场分布.由于这是标量积分，将针对某一切向场分量(如Ex或Ey)的电磁场分布进行计算，具体RS衍射积分公式为

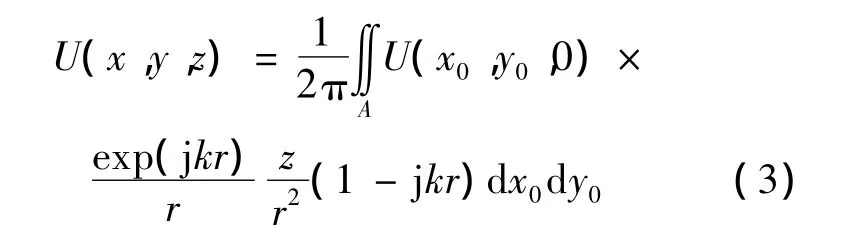
若采用物理光学积分公式，根据等效原理，将已知口面处的切向电场分布等效为表面磁流，进而利用SC方程积分求解，可以得到

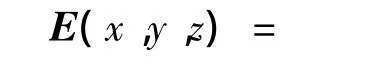
对式(4)进行矢量展开得到各分量的积分公式

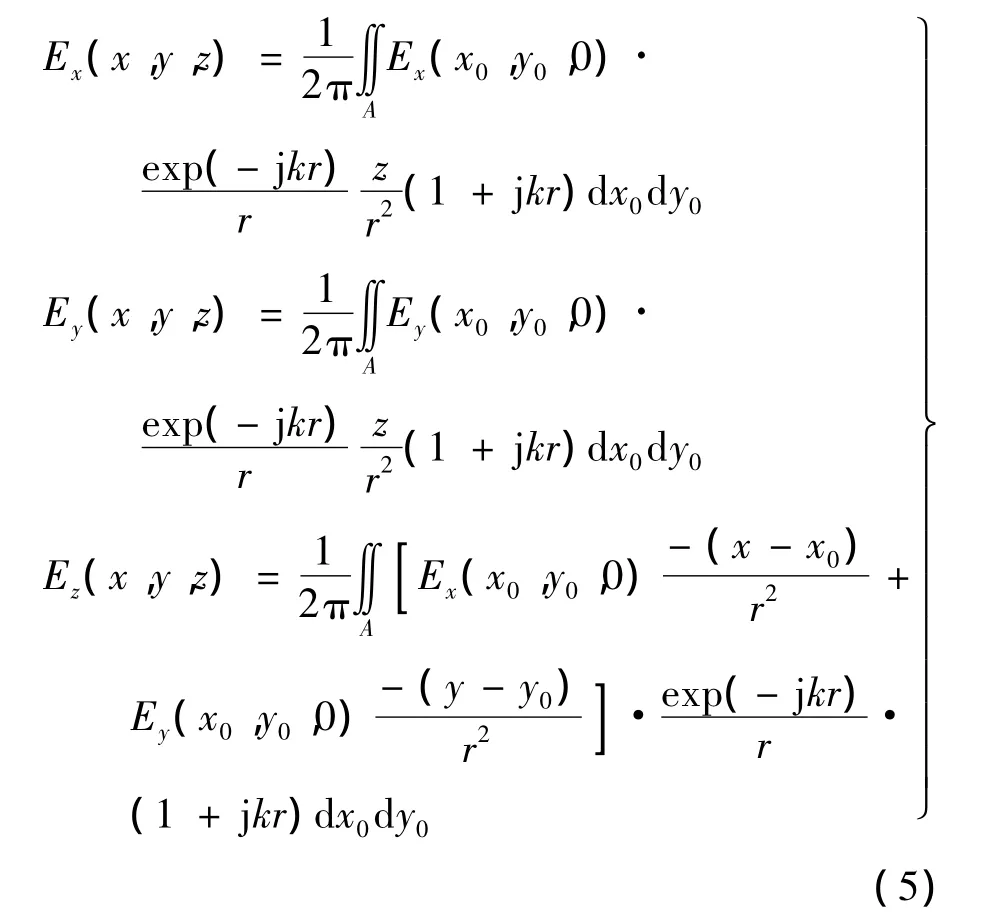
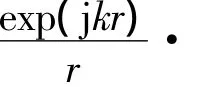
在数学推导上，造成二者最终差别的原因是二者使用的格林函数中点源波传播方向的约定不同，但是没有本质的区别.

3 实际应用的比较

以高斯波束的传播为例，定义最小束腰处的高斯分布，以向前传播一定距离处的场分布的解析解作为源分布，在此基础上分别应用RS衍射积分公式和物理光学积分公式做进一步的传播计算，如图2所示.

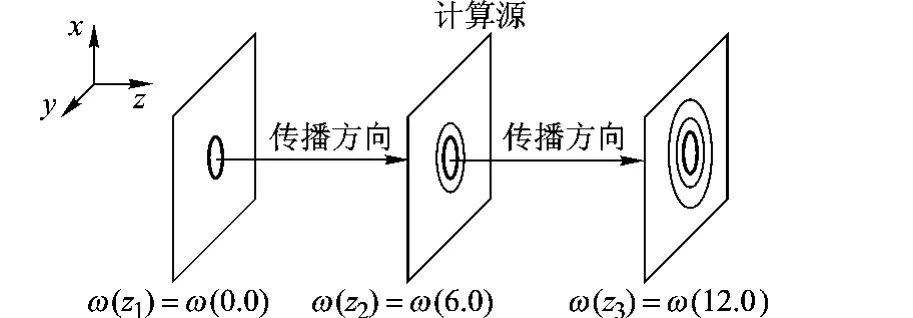
图2 以高斯波束传播为基准的仿真示意图(单位:m)

图2中源平面和计算目标平面平行于坐标平面xoy，计算参数选择为:频率f=10.65GHz(波长λ≈0.028m)，传播距离 6.0m(约为 213λ)，高斯馈源口面大小为103λ×103λ.设一个切向场分量(以Ex为例)为高斯基模分布，另一个切向场分量为0.z=0处高斯波束束腰为 ω(0)=7.1λ，采样间隔d s=λ/3.5.不失一般性，以下只针对切向场分量Ex进行仿真计算，同时选取高斯波束传播的解析解作为参考.

图3给出了高斯波束传播至z=6.0m处解析解的场分布.按照图2的模型以此为计算源，分别使用式(3)和式(5)，来计算波束传播至z=12.0m处的Ex分量场分布，计算结果如图4和图5所示.

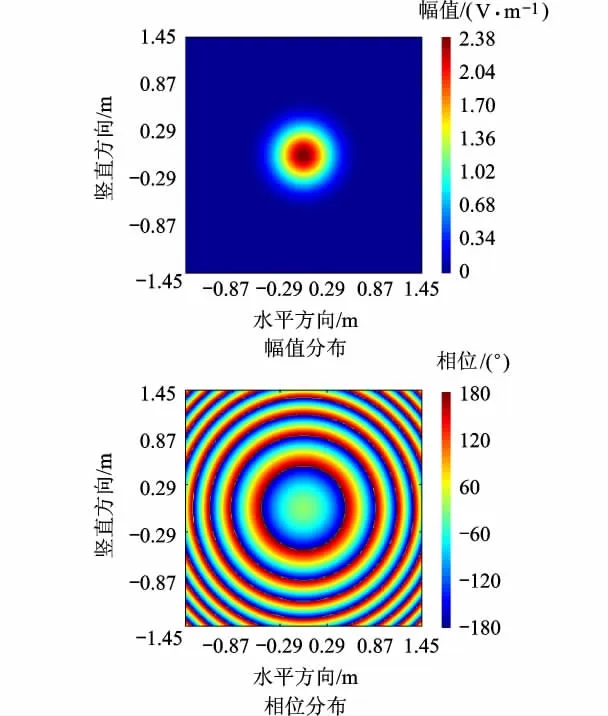
图3 高斯波束传播至z=6.0m处的解析解

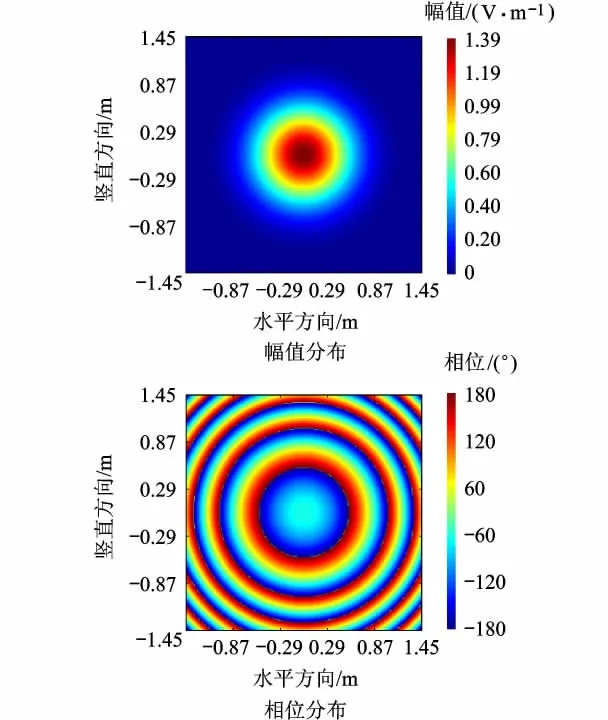
图4 物理光学积分公式计算z=12.0m处的场分布

图5 衍射积分公式计算z=12.0m处的场分布

两种不同方法的积分计算，目的都是得到z=12.0m处的场分布.然而通过计算结果与图6和图7所示的高斯波束传播解析解对比发现:物理光学积分公式完成了预期的任务，而RS衍射积分公式则是进行了一次“倒推”的计算，即由z=6.0m处的场分布倒推得到了z=0.0m处的场分布，而不是由z=6.0m处继续传播到z=12.0m处.分别对比图4与图6，图5与图7的场分布可以看出，通过两种积分方法计算求得的电磁场和解析解具有非常高的一致性.

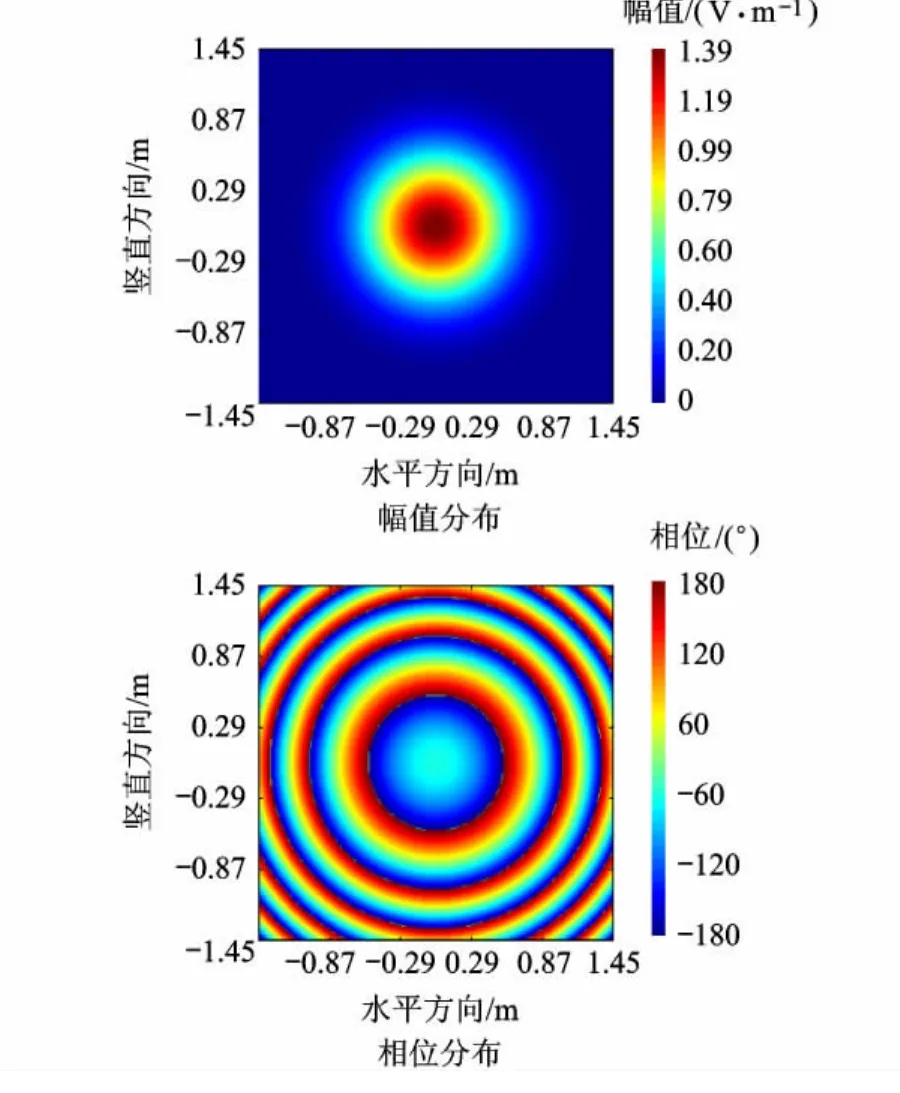
图6 高斯波束传播至z=12.0m处的解析解

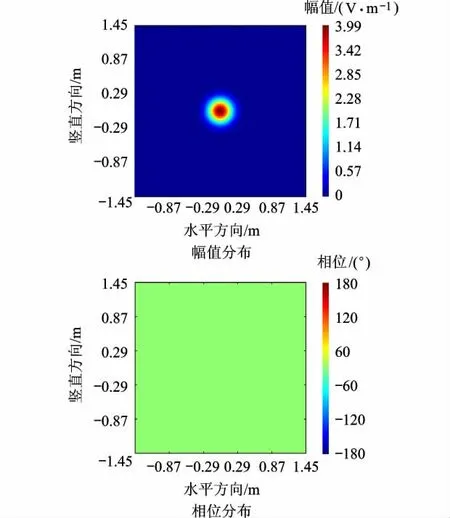
图7 高斯波束在z=0.0m处的解析解

由上述计算结果可以看出，在两种不同积分方法的应用中遇到了一个关于传播方向和计算方向的问题.在计算中，假设的传播方向是沿+z轴，而设定的计算方向也是沿+z轴，显然期望计算方向与假设的传播方向相一致，以得到想要的结果.在运用物理光学积分公式时，这种一致性是满足的;而在使用RS衍射积分公式时发现，实际的计算方向和设定的传播方向并不一致，即实际计算是沿着与设定的波束传播方向相反的方向进行的.也就是说，在使用RS衍射积分公式时，没有达到“往前传播”的计算目的，反而实现了“往后倒推”的计算.从本质上讲，造成这一差异的关键在于二者使用了不同形式的空间格林函数:

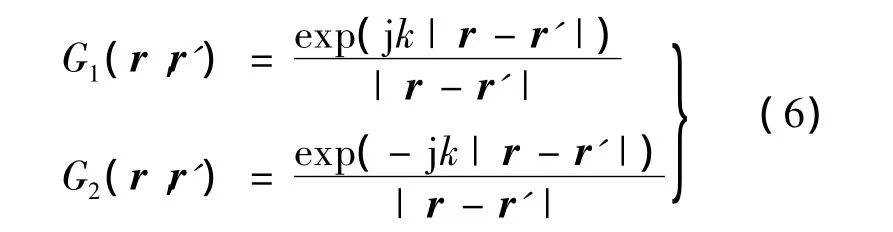
从而将RS衍射积分和物理光学积分的使用区别起来.二者的一致性是指它们都可以模拟电磁波的传播，但前提是要界定方向:这里认为衍射积分可以处理类似于倒推运算的“逆”传播，而物理光学积分则给出了电磁场“正向”传播的准确结果，如图8所示.

在使用衍射积分公式时所体现出的“倒推计算”的效果，具有重要的实用价值.例如，在确定反射镜天线系统的定向干扰源时，可以以天线口面的测试数据出发，通过倒推计算将干扰源从天线系统中“分离出来”.同时如上文中所提到，这两种积分公式在处理平行平面间的电磁场传播时所出现的卷积形式，可以使用快速傅里叶变换来加速计算，从而可以提供一种快速的计算分析手段［7，14］.

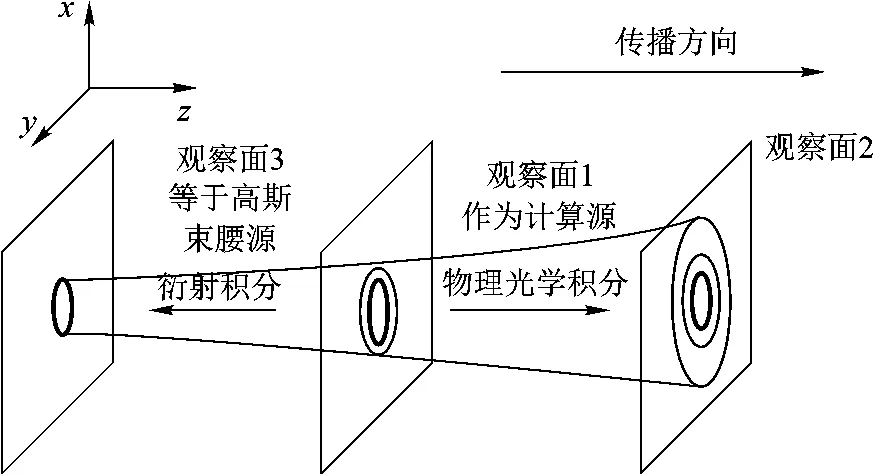
图8 衍射积分和物理光学积分计算电磁波传播的区别

4 结论

尽管物理光学积分公式和瑞利索莫菲衍射积分公式从建立的物理概念和推导过程上并不十分相近，但其最终的积分公式却有着一致的形式，数学上的区别在于采用了不同形式的空间格林函数.而从二者处理高斯波束传播的仿真算例中可以看出，物理光学可以用于“正向”的口面场传播计算，而衍射积分方法则可以用于“倒推”的口面场传播计算，这为天线系统分析等领域提供了一种方便的分析方法，具有一定的工程意义和应用价值.

References)

［1］ Goldsmith P F.Quasi-optical techniques［J］.Proceedings of the IEEE，1992，80(11):1729 －1731

［2］ Martin D H，Bowen JW.Long-wave optics［J］.IEEE Trans MTT，1993，41(10):1676 －1690

［3］ Martin D H.Millimeter-wave optics and quasi-optical antenna design［C］//Eighth International Conference on Antennas and Propagation.London:IEE，1993:894 －899

［4］ Davis J G，Truscott W S.Multiple reflection suppression algorithm for terahertz quasi-optic systems［J］.Electronics Letters，2010，6(1):52 －54

［5］ Li Junchang，Fan Zebin，Fu Yunchang.The FFT calculation for fresnel diffraction and energy conservation criterion of sampling quality［C］ //Tatsuo Okada.Lasers in Material Processing and Manufacturing.Bellingham，WA:SPIE，2002:180 －186

［6］李俊昌，陈劲波，樊则宾，等.衍射的基尔霍夫传递函数及瑞利索莫菲传递函数［J］.光电子和激光，2002，13(1):87－89 Li Junchang，Chen Jinbo，Fan Zebin，et al.The Kirchhoff transfer function and Rayleigh-Sommerfeld transfer function of diffraction［J］.Journal of Optoelectronics and Laser，2002，13(1):87 －89(in Chinese)

［7］何国瑜，卢才成，洪家才，等.电磁散射的计算和测量［M］.北京:北京航空航天大学出版社，2006:224－226，364－368 He Guoyu，Lu Caicheng，Hong Jiacai，et al.Electromagnetic scattering computations and measurements［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2006:224 －226，364 －368(in Chinese)

［8］ Liu Daqing，Wang Haogang，Li Huan.Tackling the slow attenuation of the spectral-domain green’s function in sommerfeld integrals［C］ //International Conference on Microwave and Millimeter Wave Technology.Piscataway，NJ:IEEE，2010:110 －112

［9］ Pouliguen P，Hémon R，Damiens J F.Physical optics for large scale electromagnetic scattering problems［C］//Proceedings of the Fourth European Conference on Antennas and Propagation.Piscataway，NJ:IEEE，2010:1 －4

［10］ Legault SR.Refining physical optics for near-field computations［J］.Electronics Letters，2004，40(1):71 －72

［11］ Cariou R.3D near field far field correction using the approximations of the physical optic［C］//Antennas and Propagation Society International Symposium.Piscataway，NJ:IEEE，2009:1 －4

［12］邓小玖，李国祥.平面孔的远场矢量衍射理论及其标量近似［J］.合肥工业大学学报，2000，23(6):999 －1002 Deng Xiaojiu，Li Guoxiang.The vector theory and its scalar approximation of the diffraction at a plane aperture in the far-field［J］.Journal of Hefei University of Technology，2000，23(6):999－1002(in Chinese)

［13］谢敬辉，廖宁放，曹良才.傅里叶光学与现代光学基础［M］.北京:北京理工大学出版社，2007:65－70 Xie Jinghui，Liao Ningfang，Cao Liangcai.Fundaentals of Fourier optics and contemporary optics［M］.Beijing:Beijing Institute of Technology Press，2007:65 －70(in Chinese)

［14］ Shen Fabin，Wang Anbo.Fast-Fourier-transform based numerical integration method for the Rayleigh-Sommerfeld diffraction formula［J］.Applied Optics，2006，45(6):1102 －1110