基于导频辅助的定时与载波同步环路设计
晏 辉 张忠培
(电子科技大学通信抗干扰国防重点实验室,成都 611731)
同步技术是接收机中的一项关键技术[1].由于相干通信系统必须在进行同步后才能正确地解调数据,因此同步模块的性能直接影响接收机的性能.数字接收机中的同步模块主要包括载波与定时同步.定时同步用以估计由于采样时钟造成的时偏,通过内插或匹配滤波的方式得到最佳采样点消除由时偏而产生的码间干扰.定时同步依照是否采用导频可分为数据及非数据辅助两类.非数据辅助的方式不采用导频,频带利用率高,如Gardner[2-3]及模平方和法[4].但这一类算法的同步速度慢,不适用于要求快速同步的突发通信系统.而采用数据辅助的方式可以克服这一缺点.文献[5]提出了一种最大似然定时同步算法.该算法通过将匹配滤波器采用多相实现的方式达到了把匹配及内插滤波器合二为一的效果.
载波同步是另外一类非常重要的同步模块.用以补偿由于收发两端晶振的频率漂移而造成的载波频率及相位的失调.载波同步算法同样也可分为数据及非数据辅助两类.非数据辅助的载波同步方法采用锁相环的方式实现载波同步.而数据辅助的载波同步算法则包括很多经典的算法.如最大似然、Kay[6]和 Fitz[7]法等.传统的导频都是在帧头连续放置.文献[8]定性地证明了载波同步时最优导频的放置方式为前后各一半的方式.为了实现接收机的低复杂度,本文采用文献[9]提出的一种相关函数法进行载波同步,并使用最优导频的方式来降低其估计误差.
文献[2-9]都是单独讨论定时或者载波同步.文献[10]讨论了非数据辅助的联合同步,但因为没有采用导频,所以需要采用编码辅助的方式以工作在低信噪比条件下.本文提出了一种数据辅助的联合同步算法,具体的组织结构如下:首先给出系统模型,推导了联合同步的最大似然估计原理;然后讨论了匹配滤波器的多相实现形式;接着介绍了最优导频结构,分析了载波同步的实现形式;第4节为性能仿真;最后为全文总结.
1 系统模型
图1给出了基于导频辅助同步算法的系统模型.信息比特流经过调制后与导频符号进行复用.调制后的帧长为L,导频长度为N,因此每帧的长度K=L+N.假设系统的符号周期为T,将复用后的符号流进行上采样并进行成型滤波.成型滤波器采用能量归一化的根升余弦滤波器,其单边滤波器托尾周期为LgT.实际实现时需要进行时间截断,平移及采样操作.然后对信号进行数模转换变成模拟信号.模拟信号经过加性高斯白噪声信道后由于收发两端晶振的不一致,会在射频前端引入频偏与相差,然后对信号进行采样引入采样时偏.此时得到的数字信号受到了频偏及时偏的影响,采样周期Ts=T/M,M表示采样因子.接收信号可以表示为
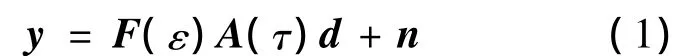
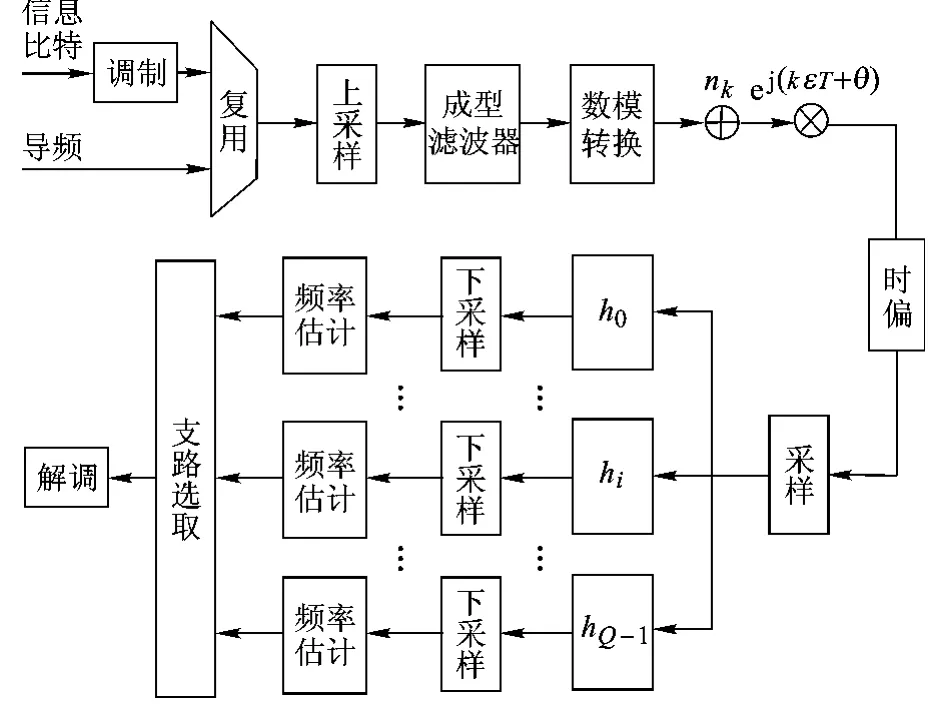
图1 系统模型
其中
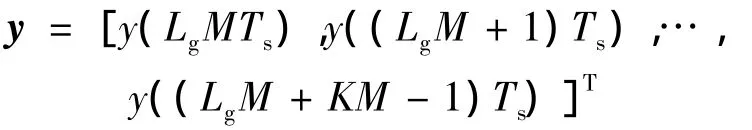
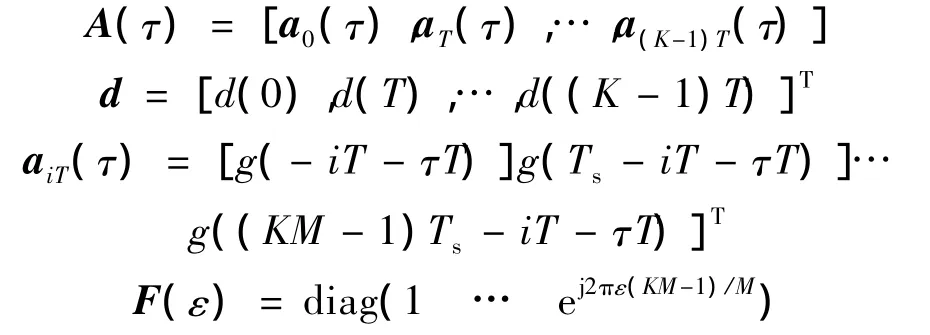
其中,ε及τ分别表示归一化的频偏及时偏;向量d表示发送的符号.去掉无关项,则似然函数可以表示为

事实上,A的列向量满足正交性,即
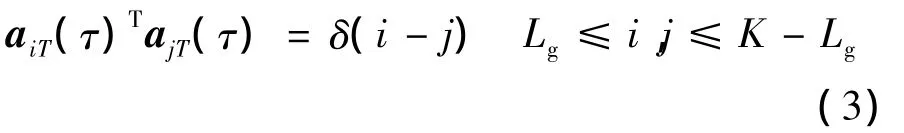
因此当 K≫Lg时,A(τ)HA(τ)≈I.所以式(2)可等效为
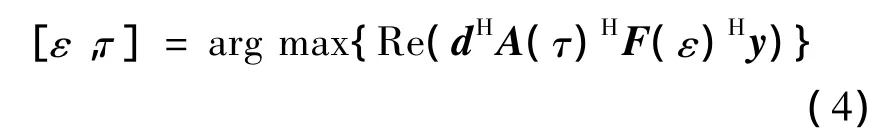
由式(4)可看出,要想同时获得时偏及频偏的最大似然估计值不仅需要进行二维搜索,而且还需要大量的过采样数据,复杂度太高.因此为了满足工程实现需求,需要对式(4)进行简化.
2 定时环路
先对接收信号进行并行匹配滤波,然后下采样进行速率转换.由M样本/符号变为1样本/符号,再进行频率估计.这样就避免了二维搜索以降低复杂度.依照文献[5]可知,并行匹配滤波器由Q个支路实现.第i条支路上多相滤波器的实现形式为

其中,-LgM≤l≤LgM;i=0,1,…,Q -1;iT/Q 代表时偏.定义Q为内插因子,很显然Q越大则精度越高,但复杂度也越大.注意每一路滤波器的长度都为2LgM+1,但每一路滤波器的输出控制相位不同.这是因为虽然每一路都要进行M倍下采样,但其采样的起始相位不同.这个相位与每个支路上对应的滤波器有关.控制相位具体的求法为:对任意一路滤波器hi,计算其与自身的卷积,找出最高峰值所在的下标Ii.表1给出了当Q=8,M=4时,各路峰值下标的取值.对于第i个支路而言匹配滤波后信号zi=hi*y,然后从第Ii个位置开始进行M倍下采样得到输出信号ri为
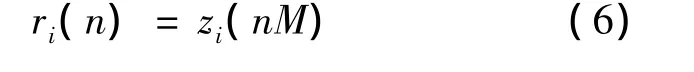
3 载波同步环路
因为ri中含有频偏信息,可以利用数据辅助的方式对其进行估计.导频的设计就成为其中的关键问题,这是因为导频结构会直接影响到频率估计算法的精度与范围.最优导频结构的定义为:当帧长K与导频长度N给定时,能使同步参数CRB(Cramer-Rao Bound)界最小的导频放置方式.文献[8]定性地证明了载波同步时最优导频的放置方式为前后各一半,称为PP(Pre-Postamble)结构.因此本文也采用这种最优导频方式,具体实现形式如图2所示.

图2 最优导频结构图
在无噪声情况下,前后两端数据经过匹配滤波后相同,因此可以利用前后两端的导频数据进行相关运算求出频率估计量.一种简单的方式是依照下式进行频率估计[11]:
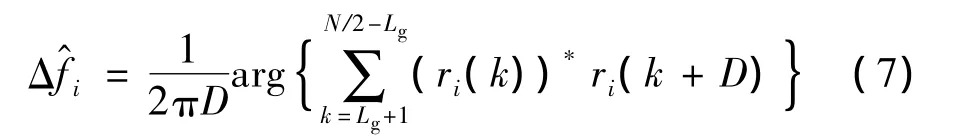
通过式(7)可看出,频率估计量的计算没有用到每段导频中的前后Lg个数据.这是因为考虑到滤波器的拖尾效应,每个匹配滤波器的输出分别与前后Lg个数据有关.因此这些数据起到保护间隔的作用,保证前后导频段中间的数据相同.通过文献[9]的分析可知这个估计量的方差较大.因此本文采用一种对相关函数求和的方法进行频率估计.该方法首先对导频序列P对接收信号进行去除相位操作,将其变为全1序列,然后再计算相关函数.具体表达式为
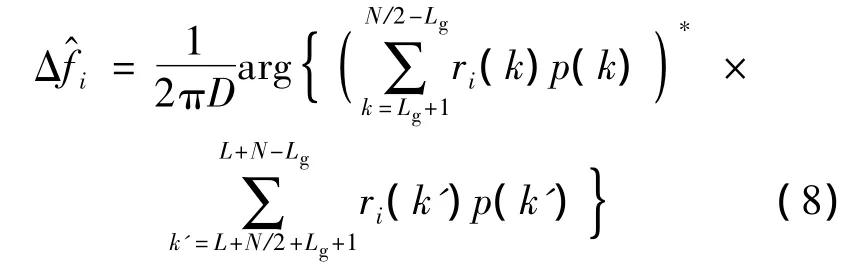
文献[9]给出了在信噪比等于ρ时估计方差的理论表达式等于:
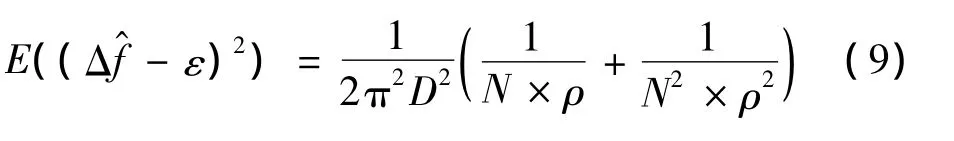
4 仿真及讨论
本文采用BPSK(Binary Phase Shift Keying)调制,滚降因子为0.35.数据长度L=2 000,仿真帧数1万,接收机过采样倍数M=4.
分别用复乘法及加法次数来衡量系统运算复杂度.假设N远大于Lg和M,并注意本文提出的导频结构实际参与运算的导频长度为N-4Lg.当采用式(4)对应的最大似然准则时需对频偏及时偏空间分别进行B点和Q点离散化.针对特定的时偏及频偏值,式(4)需要的乘法及加法次数为

而采用本文所提结构需要的乘法及加法次数为
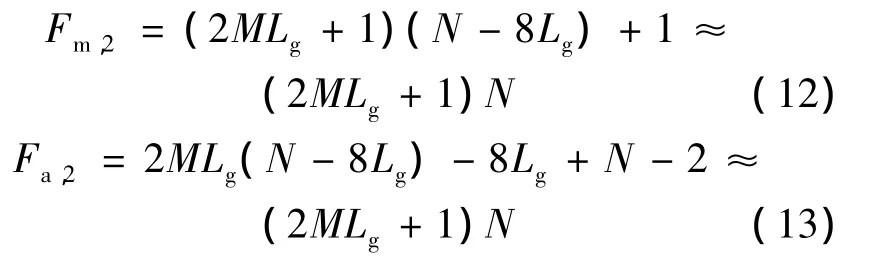
因此总的乘法及加法运算次数的比值为
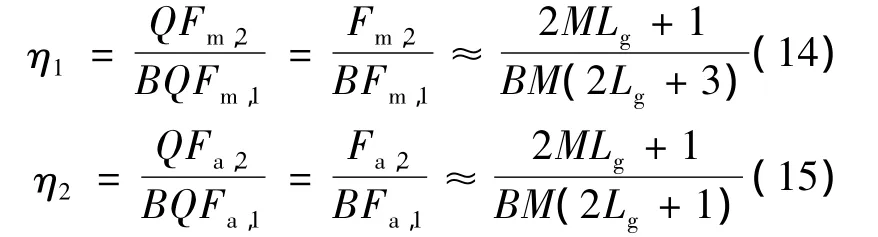
图3 对比了 N=60,τ=0.125,ε =10-4时,不同Q值对应的系统均方误差曲线图.可见,随着Q的增加,时偏的估计性能也逐步得到改善;而当Q≥32时,时偏估计的性能改善不明显;另外当Q≥16时,系统频偏的估计性能趋于稳定,不会随着Q增加而改善,即内插因子对频偏的估计性能影响较小,并且频偏实测与理论方差基本一致.
图4 给出了 τ =0.125,ε =10-4,Q=16,N 取不同值时系统估计性能图.可以看出时偏及频偏估计性能都会随着导频长度的增加而显著改善.即导频长度对同步参数估计精度有较大影响.
图5给出了不同N及Q情况下对应的误码率曲线图,并与理论误码率曲线进行了对比.可以看出,当N一定时,随着Q的增加,误码率性能得以改善.但当Q大于一定值时,系统的误码率基本上趋于理想同步;另一方面,当Q保持定值时,误码率的性能也会随着N的增加而得以改善.同样地当N大于一定值时系统性能趋于理想同步.
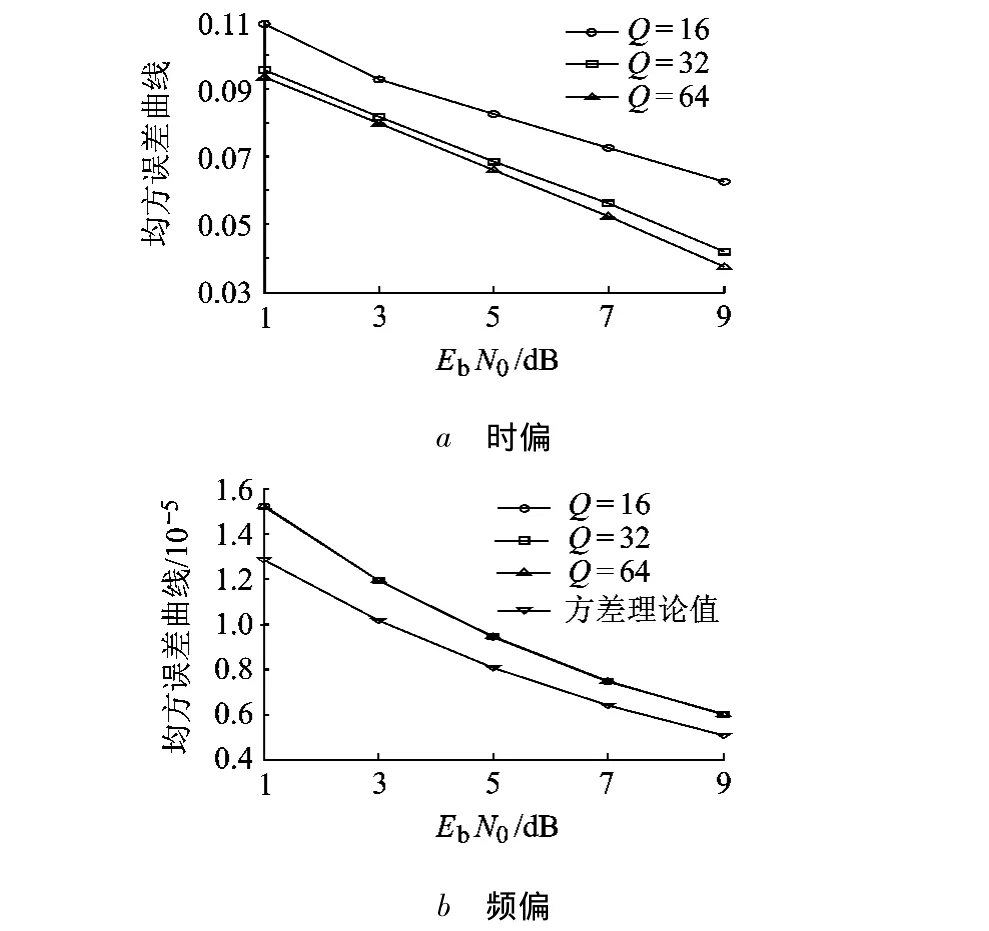
图3 N=60,不同Q对应的系统均方误差曲线

图4 Q=16,不同N对应的系统均方误差曲线
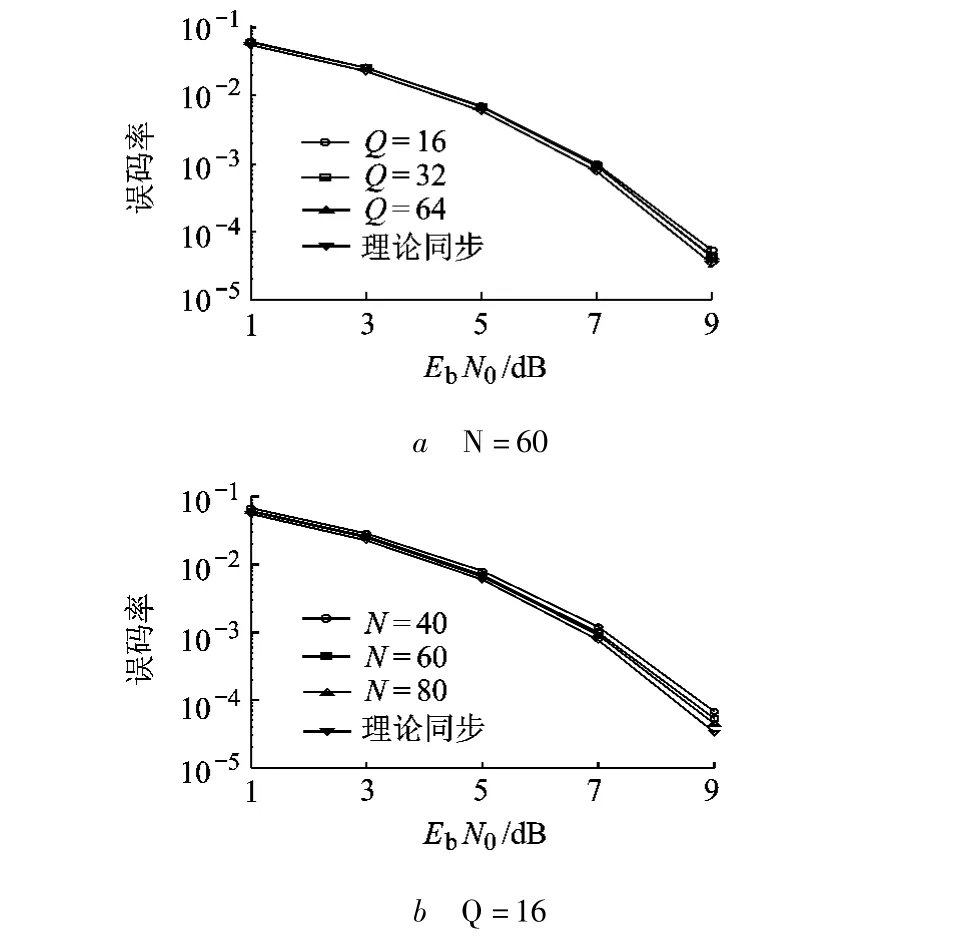
图5 两种不同情况下误码率曲线图
5 结论
本文提出了一种基于数据辅助的联合定时与载波同步算法.将运算复杂度高的最大似然问题分解成两个一维估计问题.总结全文可得到以下结论:
1)时偏估计精度主要受到内插因子Q和导频数N的影响,增加Q及N可分别提高时偏的估计精度,而频偏的估计精度主要受导频数N的影响;
2)当N和Q增大到一定值时系统的估计性能趋向于理想同步.
因此针对不同的性能要求,可合理地设置参数以满足工程需求.
References)
[1] Mengali U,Andrea A.Synchronization techniques for digital receiver[M].New York:Plenum Press,1997:1 -20
[2] Gardner F M.Interpolation in digital modems-part I:fundamentals[J].IEEE Trans Commun,1993,41(3):501 -507
[3] Erup L,Gardner F M,Harris R A.Interpolation in digital modems-part II:implementation and performance[J].IEEE Trans Commun,1993,41(6):998 -1008
[4] Oerder M,Meyr H.Digital filter and square timing recovery[J].IEEE Trans Commun,1988,36(5):605 -612
[5] Harris F J,Rice M.Multirate digital filters for symbol timing synchronization in software defined radios[J].IEEE Journal on Selected Areas in Communications,2001,19(12):2346 -2357
[6] Kay S.A fast and accurate single frequency estimator[J].IEEE Trans Acoust Speech Signal Processing,1989,37(12):1987 -1990
[7] Fitz M P.Further results in the fast estimation of a single frequency[J].IEEE Trans Commun,1994,42(2/3/4):862 - 864
[8] Yeqiu Ying,Mounir Ghogho.Optimal pilot placement for frequency offset estimation and data detection in burst transmission systems[J].IEEE Comm Letters,2005,9(6):549 - 551
[9]晏辉,唐发建,张忠培.一种基于低码率LDPC码得编码与导频联合辅助载波同步算法[J].电子与信息学报,2011,33(2):470-474 Yan Hui,Tang Fajian,Zhang Zhongpei.A joint assisted carrier synchronization algorithm with code and pilot based on low rate LDPC code[J].Journal of Electronics and Information Technology,2011,33(2):470 -474(in Chinese)
[10] Fu Honyi,Yen Kai,Yuen Sam Kwok,et al.A low complexity iterative symbol timing estimator for turbo receivers[C]//International Conference on Information,Communications and Signal Processing.Singapore:IEEE,2007:1 -5
[11] Godtmann S,Hadaschik N,Steinert W,et al.A concept for data aided Carrier frequency estimation at low signal-to-noise ratios[C]//International Conference on Communications.Beijing:IEEE,2008:463 -467

