SBAS 卫星信号的Viterbi 译码优化方案
林木龙,易清明
(暨南大学 电子工程系,广州510632)
1 引 言
SBAS(Satellite-based Augmentation System )是利用地球同步卫星(GEO)作为媒介,提供差分GPS 校正值和完好性数据的系统[1]。其数据速率由250 bit/s经由卷积编码后变换为500 bit/s, 用于与1 kHz的GPS C/A 码历元保持同步并向用户广播。SBAS 卫星信号采用(2,1,7)卷积编码,是遥测信道编码在卫星通信系统中的一种典型应用。
另一方面,用户接收到卫星信号后,必须经过正确译码恢复出卫星信息,才能顺利进行导航校正。对于SBAS 信号,传统的方法就是直接进行Viterbi 译码。考虑到实际应用中,用户需要接收多个SBAS 卫星信号,假如等接收齐500 bit的数据后才开始译码,硬件的实时性就比较差。因此,本文研究了一种优化的Viterbi 译码方案,在不降低译码性能的前提下,尽可能地满足实时性要求,并可以为硬件节省资源。
2 卷积码编码原理
卷积码是一种性能优越的信道编码,由于具备较强的纠错能力,在各种数字系统中得到了广泛应用。其一般的表示形式为(n, k,N),即由k 位信息输入编码为n 位输出,N 为编码约束长度,R =k/n是编码效率,对应的编码器有2N-1种状态。卷积编码后的n bit数据不仅与当前时刻的k 个信息比特有关,还与前N-1 个时刻的信息比特有关。编码过程中相互关联的码元有N×n 个,纠错能力随着N 的增加而增强,误码率则随着N 的增加而下降。
SBAS 卫星信号采用的是(2,1,7)卷积编码,其移位寄存器有6 级,编码器示意图如图1 所示。其中,生成多项式分别为G1=(1111001)2=(171)8,G2=(1011011)2=(133)8。

图1 SBAS 信号卷积编码示意图Fig.1 Convolutional code for SBAS signal
每输入一个比特,通过6 级移位寄存器中对应G1、G2 路径处理后,输出2 bit的码组,于是SBAS 信号250 bit/s的输入转化为了500 bit/s的输出。移位寄存器共有6 位,存储的是前6 bit的输入值,对应的状态有(000000 ~111111)64 种,当前输入的比特为0或1 将决定状态间不同的跳转,对应的2 bit输出则是由当前的输入比特及移位寄存器的状态共同决定的,即每一次2 bit 输出不仅与当前的1 bit输入有关,还与之前的6 bit输入有关。用十进制来表示状态,比如i=0 ~63 对应表示状态S 0 ~S 63,则可以用下面的公式来表示编码时寄存器状态的跳转:

式中, i 表示当前状态, %表示取模,b0 表示输入的比特值0 或1,j 为跳转后的状态。如输入b0 为0,则S 0 和S 32 转移到S0 状态,b0 为1 则有S0 和S32 转移到S 1 状态。
限于篇幅,下文以(2,1,3)的卷积编码为例,并通过直观的网格图来描述其编码过程。图2 表示的是6 bit输入对应的可能路径,其中实线表示输入0时所走的分支,虚线表示输入1 时所走的分支,编码时只需从起始状态开始依次选择路线并读出输出即可。假设从a 状态开始,输入为[1 0 1 1] ,则可由图2 中读出输出为[11 10 10 01] 。
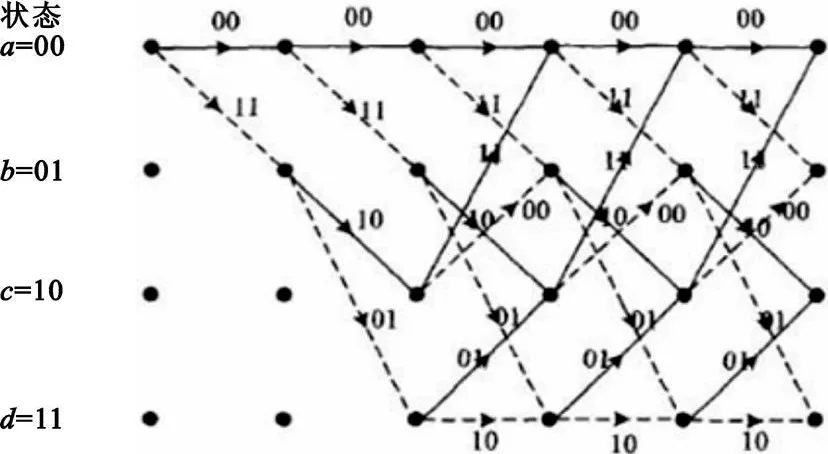
图2 (2, 1,3)卷积编码网格图Fig.2 Lattice of(2,1,3)convolutionanl code
3 Viterbi 译码原理及其优化处理
3.1 Viterbi 译码基本原理
卷积码的译码方式有门限译码、序列译码和Viterbi 译码[2]。Viterbi 译码具有最佳性能,本文对其进行研究并作优化处理,用于实现对SBAS 卫星信号的卷积码进行译码。
Viterbi 译码采用最大似然译码算法,即在所有可能的码字序列中选取一条使得似然函数极大的码字序列作为发送码的估计。仍以图2 为例,图中共有2k(N-1)=4 种状态,每个状态有2 条支路到达,也有2 条支路引出。前N-1 条连续支路的路径互不相交,即最初的2N-1条路径各不相同,当接收到第N 条支路时,每条路径都有2 条支路延伸到第N 级上,而第N 级上的每2 条支路又都汇聚到一个状态[3]。通过比较每个状态到达的2 条路径的汉明距累加值,丢弃汉明距较大的路径同时保持较小那条,最终到第N 级只剩下2N-1条路径,称之为幸存路径。在此过程中,挑选的路径及其汉明距累加值都需要保存下来。另外,由于每个状态引出2 条支路,故其后各级的延伸也都增加1 倍,但经过汉明距累加值的比较选择后,丢弃了较大的那一半,剩下的路径总数保持常数。简单来看,Viterbi 译码的过程就是一个“加、比、选”的过程,最终结果便是选择一条汉明距最小的发送路径,即路径度量最大的路径。
3.2 优化处理
标准的译码算法要求路径回到初始的全零状态,这必须在传输中最后添加N-1 个0,从而损失了(N-1)/(N+L -1), L 为输入序列长度。虽然加大L 值可以减少这种资源损失,但用于寄存路径及其度量值的存储器也随之成正比增大,同时译码延迟也会加大,故必须作出一些折衷考虑。
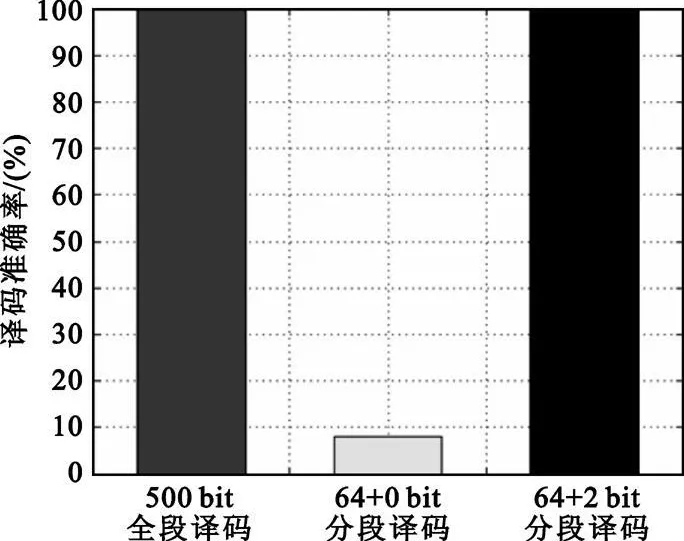
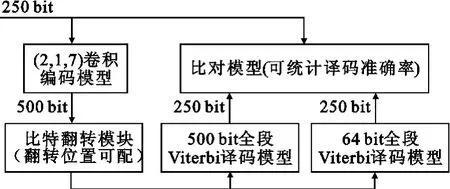
另外,对于SBAS 信号500 bit/s的数据量,若等接收齐全部信息再进行译码,中间会浪费不少时间,特别是硬件同时处理几个信号的时候。因此考虑通过截断译码器路径存储的方法,达到一边接收一边开始译码的目的,从而提高处理效率,但这样的处理显然其译码性能会有所下降。考虑到卷积码前后时刻码字的相关性,由截断造成的性能下降可以通过利用下一段数据包含的信息来补偿。经验表明,若x(每条幸存路径最近的x(x 从理论上分析,截断后的当前段码流传递给下一段截断码流的初始状态主要有两种方式:传递汉明距累加值和传递最佳路径的终止态。前者是将当前码流译码结束时保留的2N-1条路径对应的2N-1个汉明距累加值作为下一段码流译码的初始汉明距;后者则仅仅把2N-1条路径中最佳路径的终止态保存下来,作为下一段译码序列的初始态。显然,保留最佳路径终止态的方式可以大大节省硬件资源。举个例子,SBAS 信号有64 个状态,假如存储一条路径的汉明距需8 bit,存储一个状态需6 bit, 硬件同时处理5 个SBAS 信号,则传递汉明距累加值的方式需要64×8×5=2 560 bit,而最佳状态只有一个,仅需1×6×5=30 bit,这样直接可以节省2 000多个寄存器。 因此,本文根据应用的需求,对SBAS 信号的Viterbi 译码进行有性能补偿的分段处理,以期达到和500 bit全段译码相当的译码效果,同时能够减少时间和资源消耗。 在Matlab 环境下,针对1 s的数据量(即500 bit)进行Viterbi 译码。为了在较短时间内尽快处理数据,采取以“64 bit输入-32 bit输出”为单元的分段译码方式。为了确定这种分段译码方式的性能,需要通过与全段译码的性能作对比参考。具体的建模仿真思路如图3 所示。 图3 SBAS 信号Viterbi 译码建模仿真框架Fig.3 SBAS signal Viterbi decoding model 将250 bit 输入建立的(2,1,7)卷积编码器模型,输出的500 bit序列码,经过翻转位置可设定的比特翻转模块后,同时送给500 bit全段译码器和64 bit分段译码器,最后把两者的译码结果均与起始的250 bit原码比对,比较译码准确度。其中,比特翻转模块可实现500 bit序列中任意个数,任意位置处比特数值的翻转操作,目的是在译码器的输入序列当中引入错误,以500 bit全段译码的纠错能力为基准,来检测64 bit分段Viterbi 译码处理的纠错能力。 整个仿真体系中, 比对模型的做法是将随机100 次的译码结果分别同250 bit原码比对,记录下每次比对过程中错误译码的比特个数diff(1),diff(2),diff(3), …,diff(100),以及100 次译码无法全部译对的次数T ,统计出的译码准确率η定义如下: 仿真过程的具体做法是:针对比特出错的情况对64 bit进行比特补偿,即译码64+b,但输出只取前32 bit,b 为下一段64 bit开头部分的比特数,对于最后一段不够64 bit的情况,该模型对其单独处理,否则不足64 bit部分会被默认添0,导致最后译码出现几比特错误。 针对500 bit 全段译码纠错能力限度的测试,采用的是遍历1 ~500 bit位置的方法,在比特翻转模块中分别设定0 bit错误、任意1 bit错误、任意连续2 bit错误、任意连续3 bit错误、任意连续4 bit错误、任意连续5 bit错误、任意连续6 bit错误,测试结果如表1 所示。 表1 500 bit 全段译码纠错能力测试说明Tab le 1 Decoding error-correcting ability for 500 bit 由信道编码定理可知,卷积码中增大约束长度可以降低误码率,但约束长度不能取得很大,因此Viterbi 译码不可能使错误概率任意小。对于连续6 bit错误的情况,整段序列都无法保证100%能完全纠错,说明已经到了正确译码的纠错极限。同时,由表1 可知,对于连续5 bit错误以内的情况,500 bit全段序列译码仅在后面的30 bit范围内译码纠错较差。同样,对于每段64 bit的后面几个比特处,译码纠错能力也较差,但通过补偿的方法,达到和全序列译码一样的译码效果。下面给出本文的处理方法(加补偿和不加补偿两种情况)与500 bit全段译码的对比结果,见图4 ~7。 图4 最后52 bit 分段序列的不同处理结果Fig.4 Different processing results for the last 52 bit 图5 单比特错误译码结果Fig.5 One bit error decoding result 图6 连续2 bit 错误译码结果Fig.6 Two successive bit error decoding resu lt 图7 连续3 bit 错误译码结果Fig.7 Three successive bit error decoding result 上述结果相应的比特错误配置在分段序列的衔接处附近,其他位置的比特错误不用补偿也有相当的译码纠错能力。连续4 bit、5 bit错误的情况与连续3 bit错误结果类似,仿真图不再给出。仿真结果表明,对于全段译码能正常纠错的所有情况,分段加性能补偿的处理方法能够获得与之同等的译码性能,同时减少了译码过程的存储容量,这对于SBAS信号Viterbi 译码器的硬件设计具有很好的参考意义。当然,这里仅是优化方案在算法级的仿真,真正应用到硬件上还需进行充分的验证与仿真。 [1] Kaplan E D.GPS 原理与应用[M] .寇艳红, 译.北京:电子工业出版社, 2008. Kaplan E D.Understanding GPS Princip les and Applications[M] .Translated by KOU Yan -hong.Beijing:Publishing House of Electronics Industry, 2008.(in Chinese) [2] 韩可,邓中亮,施乐宁.(2,1,7)卷积码Viterbi 译码器FPGA实现方案[J] .现代电子技术,2007(15):90-92,96. HAN Ke, DENG Zhong-liang, SHI Le-ning.Imp lement method with FPGA for Viterbi decoder of(2, 1, 7)convolutional code[ J] .Modern Electronics Technique, 2007(15):90-92,96.(in Chinese) [3] 仇佩亮.信息论与编码[M] .北京:高等教育出版社,2006. QIU Pei-liang.Information theory and coding[M] .Beijing:Higher Education Press,2006.(in Chinese)3.3 仿真模型
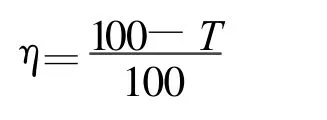
4 仿真结果