虚拟试验三维随机路面的建模
薛劲橹,王红岩,迟宝山
(装甲兵工程学院 机械工程系,北京 100072)
车辆动力学和运动学分析、构件的疲劳寿命预测、车身结构优化等研究过程所需要的各种载荷,都是在各种路面激励作用下产生的.车辆试验的路面包括两类:第一类是有确定外形的路面;第二类是符合国家公路等级标准的随机路面.在虚拟试验中,一般按照标准等级公路统计特性模拟随机路面,现有的随机路面主要是考虑纵向不平度(本文为x方向)的二维路面,忽略实际路面各单道差异,这样的路面条件必然给虚拟试验带来误差,因此本文对三维随机路面建模进行研究.
1 利用谐波叠加法建立三维随机路面
在虚拟试验环境中,一般用路面不平度功率谱密度逆推路面不平度.用标准谱逆推路面不平度的方法主要有傅氏逆变换法、白噪声法、谐波叠加法等,本文采用谐波叠加法生成三维随机路面.谐波叠加法的主要思想是将路面不平度函数表示成若干具有随机相位的正弦函数之和,其数学基础严密,适用于模拟任意类型随机路面,具有良好的适应性和较高的精确度.
单道位移功率谱密度的标准拟合表达式为[1]

式中:f为空间频率,m-1;Gd(f0)为路面不平度系数,m3,不同的路面等级对应的Gd(f0)值如表1,f0为空间参考频率,f0=0.1m-1;W 为分级路面谱的频率指数,W=2.
根据实际统计特性,路面不平度为平稳高斯过程[2],因此任意单道路面不平度均可由一系列具有随机相位的正弦函数叠加而成,即


表1 路面不平度分级标准Tab.1 Grade standard of road roughness
将频率上、下限f1,f2划分为长度是Δf的n个小区间,即f=(f2-f1)/Δf;每个小区间的中间值为fmi(i=1,2,…,n),即fmi=(fi+fi+1)/2.令fmi=fi,对应的谱密度值为Gd(fmi),Gd(fmi)可按式(1)计算;用Gd(fmi)代替Gd(f)在整个小区间内的值,则式(2)中的方差为

各个正弦函数分量为

将对应于各个小区间的正弦函数叠加,就得到二维随机路面不平度函数如下:

若建立三维路面,则路面不平度函数为

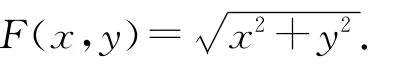
f1,f2的取值应能够覆盖车辆悬置质量部分和非悬置质量部分的固有频率,而固有频率因车而异,所以在分析不同车辆时应选取相对应的频率范围.
基于以上基本理论,本文利用MATLAB编程建立100m×4m的三维随机路面,如图1所示.由图1可知,E级路面不平度高程基本在-0.2~0.2m范围内.

图1 E级三维随机路面Fig.1 3Dstochastic road of grade E
2 路面不平度功率谱估计及相关性验证
本节通过单道不平度功率谱估计和各单道不平度相关性分析对多道随机路面谱进行验证.
2.1 基于Welch算法的功率谱估计
采用基于周期图法改进的Welch算法,对建立的随机路面模型进行功率谱估计.周期图法的基本思想是对随机信号x(n)的N点观察数据xN(n)进行傅氏变换,取其幅值的平方并除以N,作为对x(n)真实的功率谱S^(ejω)的估计,即

式中:ω为路面不平度频率;X(ejω)为xN(n)的博立叶变换.
Welch算法中,把xN(n)分成L段,对每段数据加窗后分别求功率谱密度,然后取平均值.Welch算法允许分段时数据交叠,即增大段数L,这样可以更好地改善数据方差特性,使得到的功率谱密度曲线更加平滑,但过多的分段又会使功率谱密度曲线的分辨率降低,而选择合适的窗函数可以减小频谱的泄漏,改善分辨率.经过反复对比计算,本文选择的窗函数为hanning窗,每个数据段重叠30%.
计算结果与标准等级路面功率谱密度分级图对比如图2所示,其中粗实线为建立的B级随机路面功率谱密度曲线.由图2可知,利用谐波叠加法生成的随机路面谱,与标准路面谱拟合程度较好.
2.2 相关性分析
各单道不平度的相关性即不同单道中频率为f的分量线性相关的程度[3].任取三维随机路面两条单道不平度的功率谱密度分别为Gd1(f)和Gd2(f),其互功率谱密度为Gd12(f),两单道不平度的相干函数为
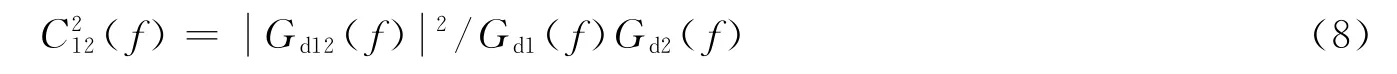
如图3所示为相干函数曲线,由图可知,由谐波叠加法生成的三维随机路面各单道间相关性很小,这是谐波函数各分量随机相位引起的.

图2 B级路面模型功率谱密度与标准谱对比Fig.2 Contrast between stochastic road of grade B and standard

图3 路面不平度相干函数Fig.3 Coherence function of road roughness
3 三维随机路面模拟软件的编制
将三维随机路面应用到动力学分析软件中,需建立相应的路面模型文件.路面模型由一系列空间三角形组成,其核心是两部分:路面节点(NODES)和路面单元(ELEMENTS).NODES是4列数组,由节点序号及该节点的x,y,z坐标构成;ELEMENTS是5列数组,由3个节点序号及该单元的静摩擦系数和动摩擦系数组成.
设三维随机路面沿纵向(车辆行驶方向)有m个节点,沿横向有n个节点,将三维随机路面投影到水平面上即为m×n点阵,将每个正方形单元划分为两个三角形单元,如图4所示.
生成NODES,将节点按照箭头“↑”所指方向排序,箭头的顺序按照从(1)到(m),即按照先纵向再横向的顺序;ELEMENTS将节点连成三角形网格,再将所有的三角形网格排序.三角形网格的连接方法如图5所示,排序也按照箭头所指方向和从(1)到(m)的顺序,其中第4列和第5列的元素为1,说明每个单元的静摩擦系数和动摩擦系数为1.排序后的NODES和ELEMENTS如图5所示.
本文编写的NODES和ELEMENTS生成算法为通用算法,只需给定纵向及横向的节点数即可生成相应的路面模型.动力学分析软件中生成的三维随机路面如图6b所示,为便于观察,选取不平度变化较大的F级路面为例.
由对比可见,三维随机路面与二维路面相比,体现了纵向、横向两个方向路面高程变化.
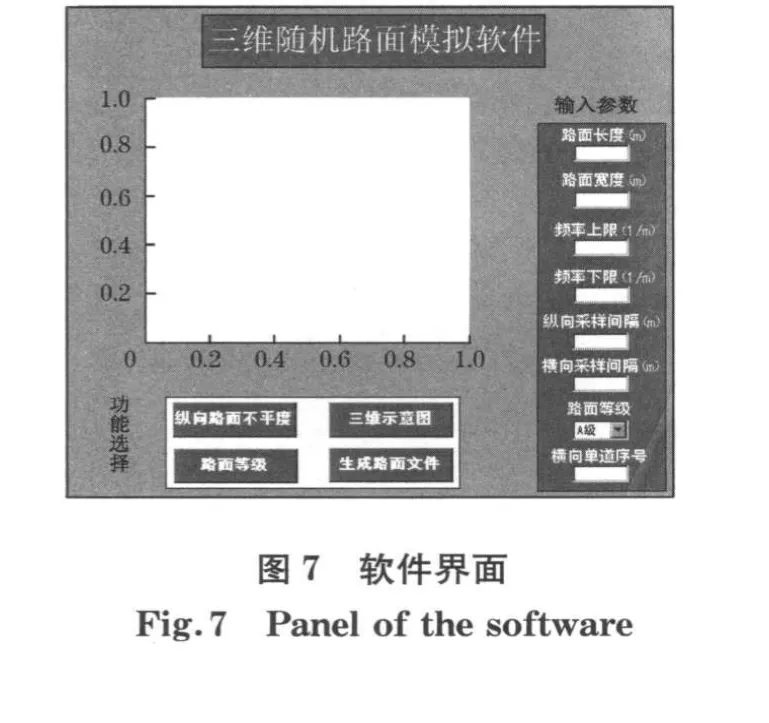
利用MATLAB图形用户界面设计工具GUI编制三维随机路面模拟软件,软件界面主要由三部分组成:参数输入部分,功能选择部分以及示意图显示部分.输入参数后,可以生成相应的路面不平度曲线、三维路面示意图以及路面功率谱密度与标准谱密度的对比示意图.此外,利用该软件还可直接生成“.rdf”格式的路面文件,用于动力学分析软件中.软件界面如图7所示.



4 随机路面激励虚拟试验
建立履带车辆动力学模型,分别利用二维和三维随机路面进行车辆直驶虚拟试验.车速为15km·h-1,仿真时间8s,路面等级为D级.设置车辆初速为4m·s-1,截取之后的匀速行驶仿真结果(1~8s的数据)进行分析.由于第一负重轮所受路面不平度冲击载荷较大,将左右两侧第一负重轮作为研究对象.
4.1 垂向位移
如图8所示,实线和虚线分别为车辆在两种路面模型直驶时,左右两侧第一负重轮质心垂向位移随时间变化曲线.
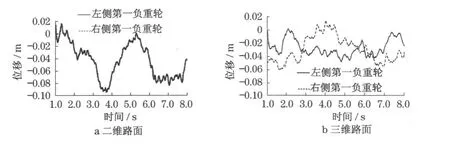
图8 第一负重轮垂向位移Fig.8 Vertical displacement of first roadwheel
由图8可知,车辆在二维路面直驶两侧支重轮位移变化完全相同,而三维随机路面与之相比可以较好地模拟两侧受路面垂向激励的差别.
4.2 侧向
图9a所示三维随机路仿真结果中,支重轮质心侧向加速度曲线震荡较为剧烈,而二维随机路面仿真结果几乎为一条直线,如图9a中粗虚线所示.将二维随机路仿真结果放大,如图9b所示,可见其加速度幅值与三维路面仿真结果相差约4个数量级.图a中较大的负重轮侧向加速度主要由三维路面不平度引起,而图b中细微的加速度变化主要是数值模拟误差造成的.

图9 第一负重轮侧向加速度Fig.9 Latitudinal acceleration of first roadwheel
图10a和b分别为图9a和b的功率谱密度曲线,二者峰值相差约7个数量级.功率谱密度反映了路面激励的能量输入,侧向加速度功率谱密度峰值出现在35Hz左右.
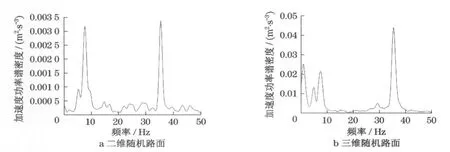
图10 侧向加速度功率谱密度Fig.10 Power spectral density of latitudinal acceleration
5 结论
(1)本文利用谐波叠加法生成三维随机路面,通过车辆虚拟试验结果,可以看出该三维随机路面可以模拟车辆垂向和侧向两个方向的载荷作用,较二维随机路面有较大改进.
(2)采用Welch经典周期图法对路面不平度进行功率谱估计,结果与标准路面谱拟合度较高,又对不同单道路面不平度的统计特性进行了相关性分析.
(3)编制了三维随机路面模拟软件,通过该软件,可直观地读取路面不平度曲线、三维随机路面示意图以及路面不平度功率谱密度与标准谱拟合图,并可直接生成适用于动力学分析软件的路面文件.
[1]长春汽车研究所.GB 7031—1986车辆振动输入路面平度表示方法[S].北京:中国标准出版社,1986.Changchun Automobile Research Institute.GB 7031—1986Vehicle vibration—describing method for road roughness[S].Beijing:China Standards Press,1986.
[2]SCHIEHLEN W,HU B.Spectral simulation and shock absorber identification[J].International Journal of Non-Linear Mechanics,2003,38(2):161-171.
[3]喻凡,林逸.汽车系统动力学[M].北京:机械工业出版社,2005.YU Fan,LIN Yi.Vehicle system dynamics[M].Beijing:China Machine Press,2005.

