用中考的眼光审视相似三角形的教学

✿五常市万宝中学 刘 玉

相似三角形是初中几何的一个重要内容，学好相似三角形不仅能使我们对图形相似有更深刻的认识，也能使我们以前学过的全等三角形的知识得以巩固和提高.正是由于相似三角形具有很强的综合性，在各种考试中，常常以图形的相似，尤其是相似三角形的知识点进行考查.

一、中考命题趋势

相似三角形在近年来各省、市的中考试题中所占的比例较高，主要考查三角形相似，线段的倍分，及等积式、等比式，求线段的比、面积的比等.其中求线段的比、面积的比，常以选择题、填空题的题型出现；论证线段的倍分、等积式、等比式，常以证明和说理题型出现；以相似图形为背景，探究函数解析式及其函数最值等问题，常以解答题的形式出现，这种题型知识性、综合性强，方法灵活，常以此来构筑中考压轴题.

二、中考复习建议

1.注重基础知识.本部分的重点是相似三角形的判定与性质，应用相关定义和定理进行证明是本部分知识的难点.复习时教师要注意引导学生分析证明思路，引导学生进行转化，帮助学生克服难点.

2.注意联系实际.相似是生活中常见的现象，在复习中，要通过复习相似的相关知识，从实际生活中发现数学问题，运用数学知识解决实际问题.

3.重视知识间的联系.在中考综合题中，经常涉及有关相似的内容，所以在复习中，要注意把相似与圆、函数等内容联系起来.

4.重视数学思想方法的渗透.本部分主要涉及的数学思想方法有类比、转化、分类讨论等，复习时要充分注意数学思想方法的渗透.

5.把握好复习难度.复习时不要过分追求难题的训练，要注重基础知识的理解和掌握，根据学生掌握知识的实际情况，由易到难，循序渐进.

三、中考考点透视

考点1：考查三角形相似

如下图，先把一矩形ABCD纸片对折，设折痕为MN，再把B点叠在折痕线上，得到△ABE.过B点折纸片使D点叠在直线AD上，得折痕PQ.

（1）求证：△PBE∽△QAB；

（2）你认为△PBE和△BAE相似吗？如果相似给出证明，如果不相似，请说明理由；

（3）如果沿直线EB折叠纸片，点A是否能叠在直线EC上？为什么？

分析：（1）利用有两个角对应相等的两个三角形相似可以证明△PBE∽△QAB；（2）△PBE和△BAE中，有一对相等的角即∠ABE＝∠BPE＝90°，只要再证得两个三角形夹相等角的两边对应成比例即可.

证明：（1）∠PBE+∠ABQ＝180°-90°=90°，

∵∠PBE+∠PEB=90°，∴∠ABQ=∠PEB.

又∵∠BPE=∠AQB=90°，∴△PBE∽△QAB.

（2）△PBE和△BAE相似.

∵∠ABE＝∠BPE＝90°，∴△PBE∽△BAE.

（3）如果沿直线EB折叠纸片，点A能叠在直线EC上.

由（2）得∠AEB＝∠CEB，又AB⊥BE，

∴EC和AE能重合，从而点A能叠在直线EC上.

解析：与相似三角形有关的问题，要善于寻找、发现相等的角.得出两角相等的有效途径主要有：公共角相等、对顶角相等、同角（或等角）的余角（或补角）相等、高线（或垂直）有直角相等.另外，应用“两边对应成比例且夹角相等的两个三角形相似”来判定两个三角形相似时，所需要的对应边之间的比例式，往往通过证明另两个三角形相似，根据相似三角形的对应边成比例得到.

考点2：考查相似三角形的判定与性质

例2：（1）如下图，⊙O的直径AB为10 cm，弦AC为6 cm，∠ACB的平分线交AB于E，交⊙O于D.求弦AD、CD的长.

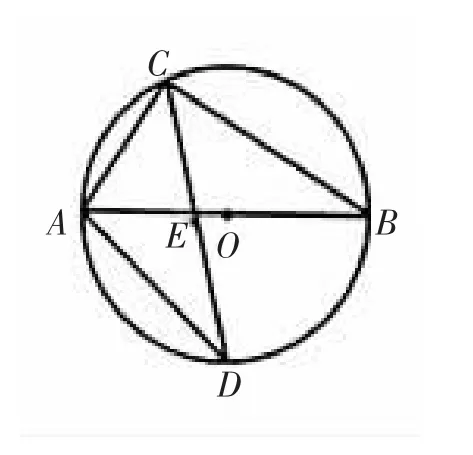
分析：由于AB是⊙O的直径，∠ACB的平分线交AB于E，所以连接BD后，可知△ABD为等腰直角三角形，从而可求出BD的长.由问题可知，图形中的所有线段均可求长，由于CD是∠ACB的平分线，所以可通作辅助线构造相似三角形求得AE或BE的长，再利用△DAE∽△DCA或△ACD∽△ECB，或△ADE∽△CBE均可求得CD的长.

解：∵AB是直径，∴∠ACB=90°.

于是在Rt△ABD中，

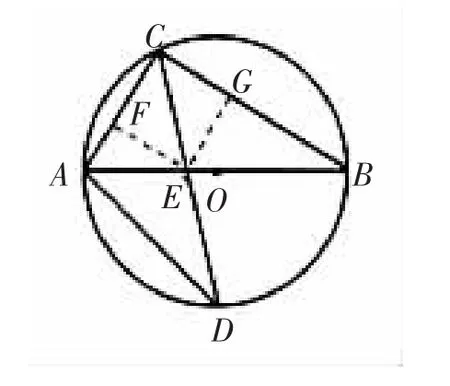
如下图，过E作EF⊥AC于F，EG⊥BC于G，F、G是垂足，

则四边形CFEG是正方形.

设EF=CF=x，

∴△DAE∽△DCA，

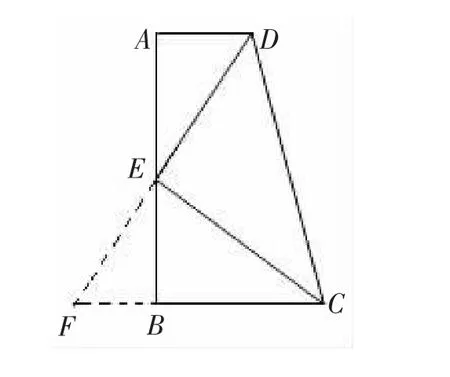
（2）如下页上图，在直角梯形ABCD中，AD∥BC，∠B= 90°，E为AB上一点，且ED平分∠ADC，EC平分∠BCD，则下列结论中正确的有（ ）.

A.∠ADE=∠CDE B.DE⊥EC

C.AD·BC=BE·DE D.CD=AD+BC

解析：由ED平分∠ADC可知∠ADE＝∠CDE，故A正确；由AD∥BC得∠ADC＋∠BCD＝180°，又∵∠EDC＝·∠ADC，∠ECD＝∠BCD，∴∠EDC＋∠ECD＝90°，∴DE⊥EC，故B正确；易证△ADE∽△BEC，∴AD∶BE＝DE∶EC，∴AD·EC＝BE·DE，故C不正确；延长DE交CB的延长线于点F，易证△ADE≌△BFE，得AD＝BF，∴CD＝CF＝BC＋BF＝AD＋BC，故D正确.因此，本题应选A、B、D.

解析：本题是一道多选题，是近年来在中考数学中出现的一种新题型.本题考查的知识点较多，有平行线的性质，角平分线定义，全等三角形的判定和性质，等腰三角形的性质，相似三角形的判定和性质等，能否熟练应用这些定理是解题的关键.

考点3：考查相似三角形在位似图形中的应用

例3：如图，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB的顶点都在格点上，请在网格中画出△OAB的一个位似图形，使两个图形以O为位似中心，且所画图形与△OAB的位似比为________.

分析：位似图形一定是相似图形，但相似图形不一定是位似图形.本题可根据位似图形及相似三角形的知识求解，应注意所画三角形的顶点要在格点上.

解：如图，△OA′B′即为△OAB的位似图形，位似比为2∶1.

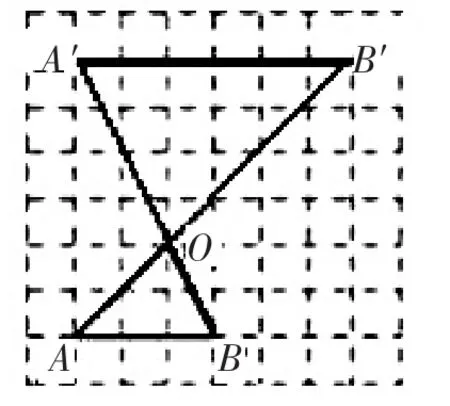
解析：本题考查了位似图形的概念以及基本作图。解答时要注意审题，顶点要画在格点上.需要提醒的是在进行位似变换时，要注意分两种情况解答：一种是位似图形有位似中心同侧，另一种是位似图形在位似中心的异侧.本题之所以画△OAB的位似图形时只画一个，是因为同侧的位似图形，顶点不在格点上，不合题意，故没有画出.

考点4：考查相似三角形中的条件探究型问题

例4：如下图，在矩形ABCD中，AB＝4，AD＝10，直角尺的直角顶点P落在AD上（点P与A、D不重合），一直角边经过点C，另一直角边与AB交于点E.（1）当∠CPD＝30°时，求AE的长；（2）是否存在这样的点P，使△DPC的周长等于△AEP周长的倍整数？若存在，求出DP的长，若不存在，请说明理由.

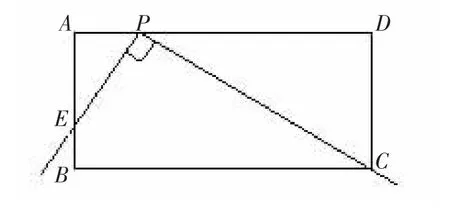
分析：（1）当∠CPD＝30°时，可算出PD、PC的长，后可得AP的长，在Rt△APE中可利用三角函数或相似求出AE的长；（2）属于一个条件探究性问题，可先将结论作为条件来探索，如能得到合理的结论，则说明存在，反之则不存在.

解：（1）在Rt△PCD中，

（2）假设存在满足条件的点P，设DP＝x，则AP＝10-x,由Rt△AEP∽Rt△DPC知=2，所以=2，解得x＝8，此时AP＝2，AE＝4，符合题意.