多TMD控制下超高层建筑风振响应的快速算法及其应用*

李小康 谢壮宁 王湛

(华南理工大学亚热带建筑科学国家重点实验室，广东广州510640)

作为一种能量耗散装置，调谐质量阻尼器(Tuned Mass Damper，TMD)可用来增加结构的总阻尼从而抑制结构振动，目前在大型复杂土木结构的风振控制中获得较为广泛的应用.TMD的设计制作有赖于对 TMD风振控制效果的精确计算，因此TMD风振控制计算引起了结构风工程界的广泛关注［1-6］.目前，对高层建筑TMD风振控制机理与计算方法的研究已趋成熟，但相关工作主要集中在顺风向控制，针对横风向风振控制的研究较少.尽管就控制机理本身，横、顺风向并无本质差别，但由于荷载形成机理的差异导致横风向气动荷载要远比顺风向复杂，目前尚无法类似于顺风向给出统一的表达形式.风洞试验作为唯一可精确获取结构横风向气动荷载的有效手段被广泛应用，但针对试验数据的风振控制计算分析则少有研究.随着结构高度超过200m，结构横风向响应逐渐超越顺风向成为控制风向，因此对横风向风振控制的计算研究更具实际意义和工程价值.

针对任意复杂形式的大型空间结构，文中提出一种多调谐质量阻尼器(MTMD)风振控制的快速算法，该方法计算效率高、内存消耗少，属于一种精确算法，使得需要大量计算的单调谐质量阻尼器(STMD)参数分析成为可能，同时也可进行更为复杂的 MTMD风振控制的精确计算分析.文中以439m高的深圳京基金融中心(KFT)为背景进行风致响应及控制的计算，分析了STMD的频率、阻尼比和质量等参数对风振控制效果的影响，并对不同形式MTMD的控制效果进行详细的分析计算和讨论.

1 方法概述

受l个TMD控制的高层建筑，其风振反应的运动方程可表示为

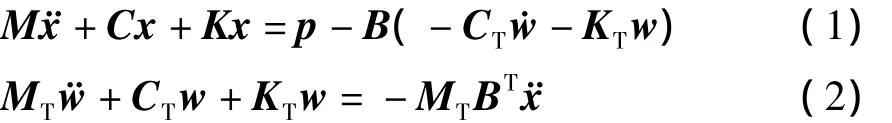
式中:M、C、K分别是结构系统的质量、阻尼及刚度矩阵;MT、CT、KT分别表示TMD系统的质量、阻尼及刚度矩阵;B为N×l阶TMD系统的位置指示矩阵，bji=δjk(i=1，2，…，N);x为结构位移向量;w为TMD相对位移向量;p为气动力向量.

令x=Φq，其中Φ表示结构模态矩阵(N×r阶)，q为前r阶模态响应向量，由振型分解法可得受控结构在模态坐标下的运动方程:

式中，ζs、ωs分别为前r阶结构模态阻尼比和模态频率矩阵，ζT、ωT分别为l阶TMD阻尼比和频率矩阵(均为对角阵)，g=ΦTp为广义力向量，，Mp=ΦTMΦ为模态质量矩阵.

对式(2)进行简单处理，TMD运动方程可写为

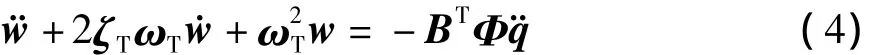
对于式(3)，由于方程右边第二项的存在，使得受TMD控制下的结构运动方程不能简单地转化至频域内进行求解，常用的办法是将式(3)中方程右边的第二项移动至方程的左边，将变化后的式(3)与式(4)共同组成另一方程组进行求解，但当式(3)中结构多阶模态参与响应贡献时，组装后方程组再次出现需要解耦的问题.尽管目前对于高层建筑的风振控制计算可进行适当简化，采用一阶模态响应近似估算结构总响应［4］，但这种处理会影响其普适性，尤其是对于大型复杂空间结构(也包括考虑横、顺、扭耦合作用的超高层建筑)，仅考虑一阶模态显然是不够的.

采用文献［7-8］中的基本思想推导结构在受TMD控制下的结构运动方程.假定pu、qu、gu、xu和wu分别为气动力p、模态响应q、广义力g、响应x和w的截尾函数矢量，同样xu=Φqu，则有

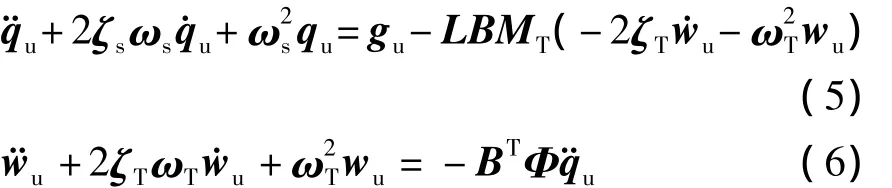
由于截尾函数矢量pu满足绝对可积条件，可对其进行傅里叶变换，有

式中，i为虚数单位;t、ω分别表示时间和圆频率变量，Pu是ω和截尾函数的截取时间长度T0的函数.同样，Gu、Qu和Wu分别表示gu、qu和wu的傅里叶变换，其表达式类似于式(7).可以证明［9］，当p为平稳随机过程时，其功率谱密度矩阵Sp为

式中，上标*表示共轭.由此，式(5)、(6)在频域内可表示为

记

hs=(-ω2+2ζsωsωi)-1(为r阶对角阵，表示无TMD控制的结构广义坐标的频响函数矩阵)，

由式(10)得

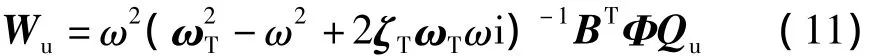
代入式(9)，有

经分析可知，式(12)中括号项的逆阵是存在的，记

它实际为TMD控制下的结构主坐标频响函数矩阵，由此式(12)可简述为

由式(7)及gu定义可知:

同时令

则TMD控制下的结构风致响应x的功率谱函数矩阵Sx可采用下式计算:

对于TMD系统本身，将式(15)代入式(11)，并定义

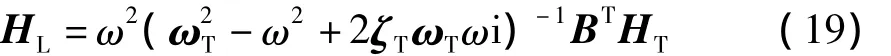
则TMD系统响应表示为

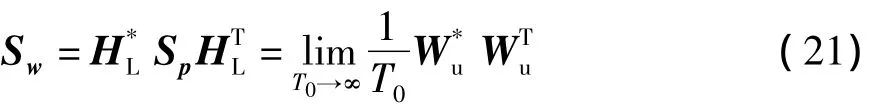
分别对结构系统和TMD系统的功率谱函数进行积分，即可获得响应协方差矩阵:同样其功率谱函数矩阵可采用下式进行计算:

由上可以看出，在无TMD控制时，方程(1)中位置矩阵B为零矩阵，方程(1)退化为无TMD控制的运动方程，可见文中算法适用于任意复杂形式的结构风致响应及TMD控制计算，属于对HEM算法［7］的扩展.同时注意到有无TMD控制的结构响应计算仅在于系统频响函数之间的区别，与无TMD控制的结构频响函数矩阵hs相比，受TMD控制的结构频响函数矩阵hT并不是对角阵，但作为一确定性矩阵而言对计算效率基本不存在影响.

特别需要指出的是，如果采用传统完全二次型组合方法进行风振控制计算，仍然会出现3个3维矩阵相乘的问题，其谱矩阵的存储需要非常大的内存空间，计算也颇为耗时，即便可勉强计算下去，计算效率也令人难以忍受［8］.

2 实例验证及分析

2.1 KFT结构特征及风洞试验简介

KFT工程的基本建筑外形如图1所示，塔楼主立面(南北立面)基本为等宽度圆弧收缩曲面，两边有1.8m悬挑翼板.图1(b)中西侧立面(东西两侧立面相同)为圆锥形平面，立面上设置遮阳构件，塔楼顶部高度为439m，从上至下依次设置5个设备层和避难层，其编号及高度如图中标注.图1(c)给出了塔楼基本平面布置及风洞试验坐标系.KFT模型采用有机玻璃制作，几何缩尺比为1∶450，模型总高度为0.976m，试验详细信息可见文献［10］.KFT风致响应计算中取结构前12阶模态进行响应计算，结构前3阶模态周期分别为7.52、7.19和3.92s，分别对应x、y和扭转方向，结构的模态阻尼比分别取为3.5%和1.5%，用于位移和结构顶部加速度计算.

2.2 STMD参数分析

在结果分析之前，定义以下基于顶部加速度的减振系数βa和顶部位移的减振系数βd:

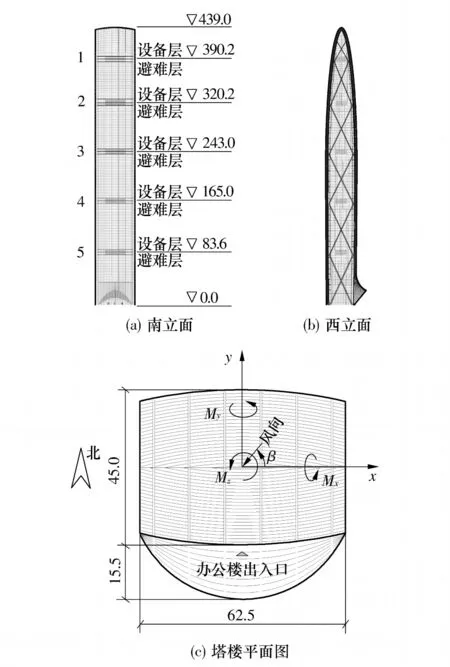
图1 建筑示意图及参考坐标系(单位:m)Fig.1 Building drawing and definition of coordinate system (Unit:m)

式中，σa，T和σa分别为10年重现期受控和不受控的结构顶部加速度标准差，σd，T和σd为100年重现期受控和不受控的结构顶部位移响应标准差.由定义可知，βa和βd越小，减振效果越好.为表述简洁，下文出现的加速度响应均为10年重现期结果，位移响应均为100年重现期结果.

首先考虑STMD情况，对受控情况下的结构风致响应进行计算，分析STMD各参数对控制效果的影响.结果包含结构系统各自由度位移、加速度及等效静风荷载响应和TMD系统的位移、加速度响应等，限于篇幅，文中仅给出横风向响应结果.

在频率比固定不变的情况下，首先考察ξT对控制效果的影响，结果如图2所示，其中质量比UT分别取值为0.005、0.010、0.015，对应实际质量为520、1039、1559t，频率比fT/f0=1(STMD频率fT与结构受控横方向第1阶固有频率f0之比，f0=0.139)，ξT取值范围为0～0.1.

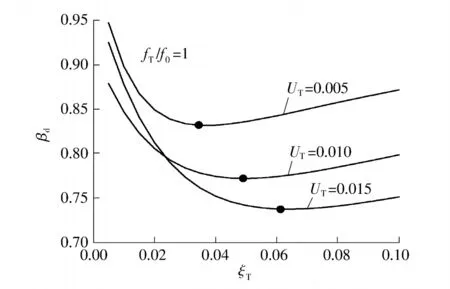
图2 减振系数随STMD阻尼比的变化Fig.2 Vibration reduction of coefficient with.STMD damping ratio

由图2可见:随ξT增加，βd呈现先减小后增大的趋势;当ξT太小以致接近零时，控制效果最差;存在一个ξT最优值，当ξT超过最优值继续增大时，位移的控制效果反而降低，但变化幅度并不显著，特别是随着UT的增加，反映控制效果的参数βd变化曲线趋于平缓，且由图2可以看出，随着UT的增加，ξT最优值也逐渐增加，当UT取0.015时，最优的ξT接近0.06.

在保证一定控制效果的条件下，实际TMD设计中宜取较大的ξT以保证TMD本身有足够的能量耗散性能而不至于由于过度的振荡产生疲劳破坏而使TMD失效，当然TMD本身还会有限位装置防止这种情况发生.因此根据图2，在文中后续的计算分析中，均按照ξT=0.065进行计算.

图3给出了STMD控制下结构均方根位移响应随STMD频率比fT/f0的变化情况，fT/f0取值范围为0.1～2.0.

图3 减振系数随STMD频率比的变化Fig.3 Vibration of reduction coefficient with STMD frequency ratio

由图3可见:(1)随UT的增加，βd逐渐减小，STMD的控制效果增加;UT=0.015时，βd最小为0.723，但在实际工程中多方面因素限制了TMD质量不可能过大，同时过度增加质量会影响整体结构的动力参数指标，使得计算结果失真.(2)在ξT不变的前提下，随着fT远离结构固有频率值，βd增加，控制效果减弱;fT在结构固有频率附近时，控制效果最佳，但由于阻尼的影响，最佳控制效果的fT略小于结构固有频率f0.(3)βd对fT的变化较为敏感，当fT/f0小于0.5或大于1.5时，βd均接近1;STMD的控制效果仅在较小的fT范围内较好.

图4给出了结构受控前后结构顶部位移响应的功率谱密度在不同坐标系统下的比较结果，为了直观起见，图中功率谱密度的变量改用频率f表示，竖线表示结构第2阶固有频率为0.139 Hz(对应结构横风向第1阶频率).由图可见，横风向响应的共振部分远大于背景部分，在TMD作用下，响应的共振部分被抑制，处于共振区(结构固有频率附近范围)的响应功率谱密度函数值急剧减小，使得结构风致响应显著降低.由图4可以清晰地看出，TMD装置只能控制其对应模态频率附近的功率谱密度值.

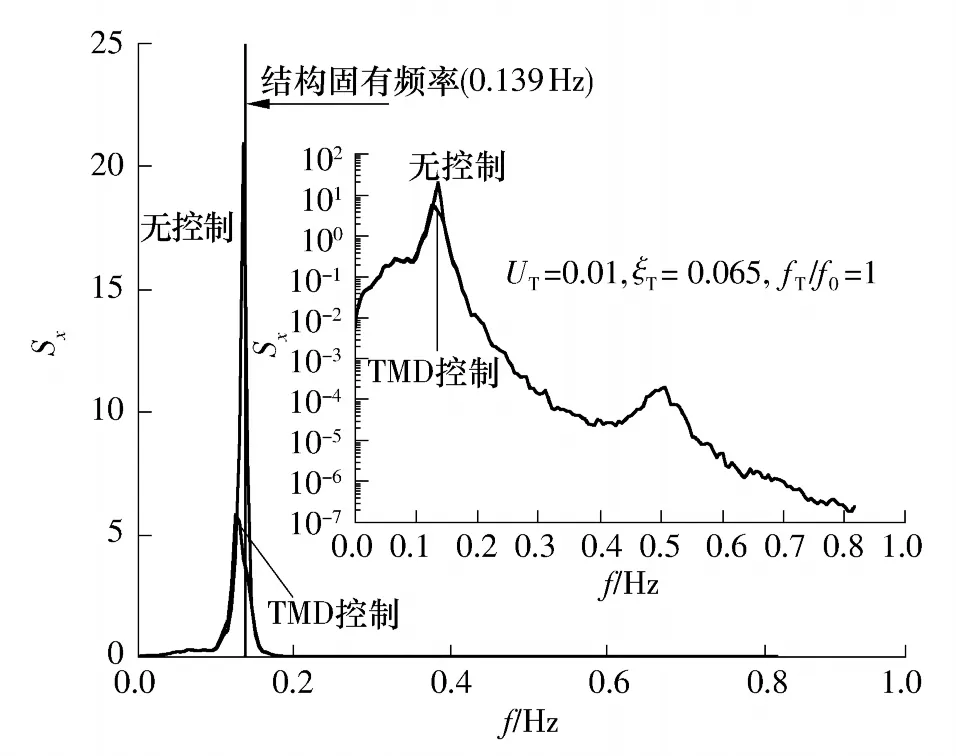
图4 结构顶层位移响应功率谱密度函数Fig.4 PSD of displacement response at the top floor of the building

2.3 MTMD参数分析

2.3.1 不同楼层MTMD的控制效果

由于超高层建筑的风振响应一般是一阶振型控制的，故在理论上将STMD置于结构顶层可以获取最佳的控制效果，但实际应用中在某些情况下，受空间、安装和结构等方面的限制，必须采用每个TMD相比更小的MTMD方式.

以KFT工程为例，改用3个质量相同的TMD，安装在在1、2、3号设备层(见图1)上，TMD的总质量比UT仍然取为0.01，每个TMD的fT/f0=1，ξT= 0.065，采用文中方法计算其控制效果，结果见表1.注意比较是基于TMD总质量一致的原则也即表中的3种控制策略的TMD总质量比是一致的，均为0.01.由表1可见，仅在设备层1安装TMD的控制效果最佳(即STMD)，βa=0.686，βd=0.778，在3个设备层均设置有TMD时，βa=0.734，βd=0.820，加速度和位移的控制效果比单个TMD方案差些，但差别不大，只有0.048和0.042.

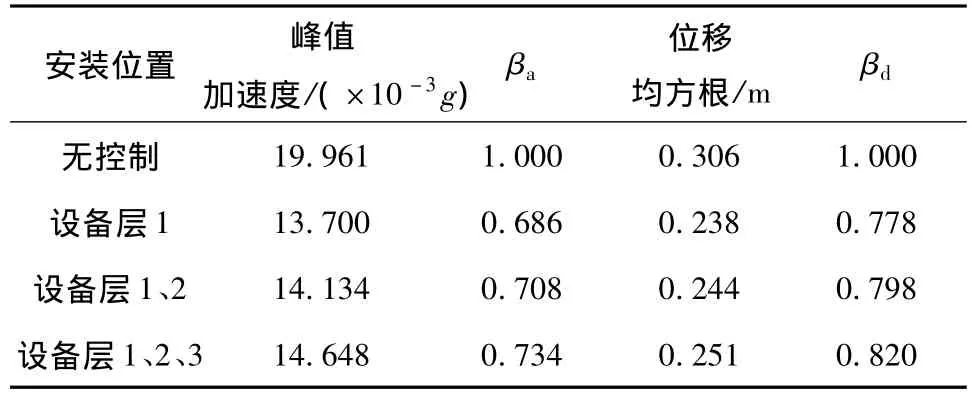
表1 不同楼层MTMD作用下结构顶部的横风向响应Table 1 Across-wind response at top with MTMD on different fcoors

虽然MTMD的控制效果不如STMD，但MTMD系统中每个TMD的体积和重量相对较小，更易于安装、实现，从整个系统上考虑，其可靠度也更好，当MTMD中某个TMD出现故障时，其它TMD依然可保持工作状态且能够取得一定的控制效果.考虑以上3个小TMD构成MTMD，在1、2、3号设备层布置3个相同的TMD，计算不同工作状态时的控制效果见表2.其中每个TMD的参数为:ξT=0.065，UT= 0.0033，fT/f0=1，工况栏中的数字表示参加工作的TMD所在的设备层号(没出现号码表示该TMD失效)，如1/2表示只有1、2设备层的TMD参加工作而3号设备层TMD失效.

表2 不同工况MTMD作用下结构顶部横风向响应Table 2 Across-wind response at top with MTMD in different experimental cases

计算结果表明，尽管MTMD中单个TMD出现故障导致控制效果有所减弱，但其他层TMD仍可起到较好的控制作用.例如，第3设备层的TMD失效时，βa=0.754，βd=0.840;即便是控制效果最好的第1设备层TMD失效，βa和βd仍有0.819和0.889，较无控制工况也分别降低了0.181和0.111.

2.3.2 MTMD频率的影响

MTMD系统中可通过对每个TMD设置不同的频率进一步扩大其控制范围.在KFT设备层1、2、3上布置不同频率的TMD组成MTMD系统，第1、2和3设备层的TMD的fT/f0分别取为1.10、1.02和0.94，UT=0.0033，ξT=0.065.同时分析在不同结构周期情况下对顶部加速度的控制效果并和STMD (fT/f0=1，UT=0.001，ξT=0.065)情况做比较，结果见图5.

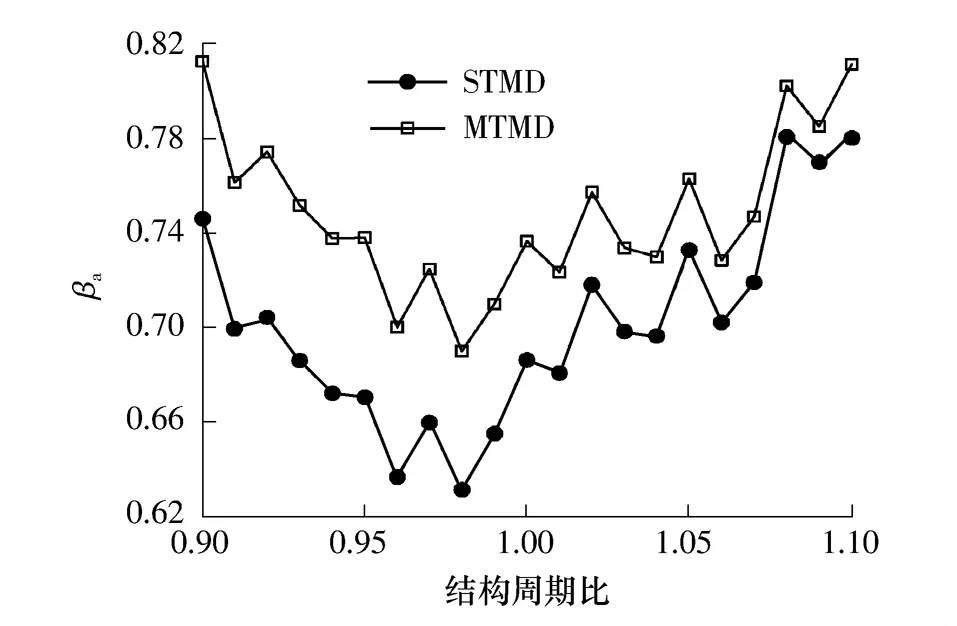
图5 减振系数随结构周期的变化Fig.5 Vibration of reduction coefficient with structural natural period

由图5可见，当结构周期比在0.90～1.10之间变化时，总的看来两种控制方式的效果随周期比变化的趋势是一样的，但MTMD的控制效果要略差于STMD的控制效果.

2.3.3 受控结构阻尼的影响

实际上，结构参数中阻尼的不确定性会远高于结构频率，假定结构周期不变，分析以上STMD和MTMD在不同结构阻尼比ζs下的结构顶部加速度的控制效果，结果见图6.

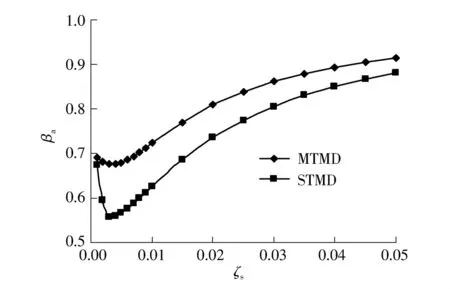
图6 减振系数随结构阻尼比的变化Fig.6 Vibration of reduction coefficient with structural damping ratio

由图6可见，在ζs＞0.003时，两种控制方案的βa均随ζs的增加而单调增加，控制效果在ζs=0.003时最好，但由于实际结构的模态阻尼比不可能小于0.003，因而图中ζs的较小值并没有太大的实际借鉴意义，可以认为结构阻尼比越小控制效果越好.

2.3.4 不同频率MTMD的全风向控制结果

以上TMD控制方法的研究主要针对0°风向角(横风向)进行，实际工程中需要对36个风向角的控制效果进行综合评判，以图5中选用的MTMD系统为例，采用文中快速算法计算KFT工程36个风向角的加速度响应，并与无控制的结果进行比较，结果见图7.

图7 全风向角下顶部峰值加速度Fig.7 Peak acceleration of structure at all azimuths

由图7可知，MTMD作用时0°和180°风向角附近(横风向)结构顶部峰值加速度比无控制时显著降低，无控时顶部最大峰值加速度为0.0229g，出现在350°风向角，主要是由于上游地王大厦的干扰引起［10］，由《高层建筑混凝土结构技术规程》［11］可知，该峰值加速度值不能满足规范中有关高层住宅舒适度的规定(不大于0.015 g)，仅满足办公要求(不大于0.025 g)，而采用MTMD控制之后，可将该风向角峰值加速度进一步降低至0.0156g，减少约32%，这也是受控结构全风向的最大峰值加速度.而在90°和180°风向角附近(顺风向)，由于MTMD并不控制该方向风致振动，受控前后响应差距不大.图7还表明，在MTMD控制下，所有风向角的结构顶部峰值加速度响应均比无控时要小.

3 结论

文中提出的多TMD风振控制响应的快速算法理论上属于一种精确算法，且计算效率高，可对任意复杂形式的空间结构进行风振控制计算.

单TMD的控制效果对TMD频率比较敏感，最佳频率比略小于1;最优的TMD阻尼比和TMD质量有关，随TMD质量的增大而增大，考虑到阻尼的耗能作用，建议采用0.065的TMD阻尼比.

在总质量相同的条件下，采用在不同楼层设置TMD方式的减振效果只比在顶层设置TMD的效果减少5%左右，两者的控制效果随结构频率和阻尼的变化规律也保持一致.

采用MTMD方案的全风向角计算结果表明，在MTMD的控制下，结构顶部峰值加速度的最大值下降30%左右，基本满足规范中高层住宅和办公的舒适度要求.

［1］ Xu Y L，Kwok K C S，Samali B.The effect of tuned mass dampers and liquid dampers on cross-wind response of tall/slender structures［J］.Journal of Wind Engineering and Industrial Aerodynamic，1992，40(1):33-54.

［2］ Ricciardelli F.A linear model for structures with tuned mass dampers［J］.Wind and Structures，1999，2(3): 151-171.

［3］ Rana R，Soong T T.Parametric study and simplified design of tuned mass dampers［J］.Engineering Structures，1998，20(3):193-204.

［4］ 瞿伟廉，陶牟华，Chang C C.五种被动动力减振器对高层建筑脉动风振反应控制的实用设计方法［J］.建筑结构学报，2001，22(2):29-34. Qu Wei-lian，Tao Mu-hua，Chang C C.Practical design method for effect of five kinds of passive dynamic absorbers on fluctuation wind-induced vibration response control of tall buildings［J］.Journal of Building Structures，2001，22(2):29-34.

［5］ Li Chunxiang.Performance of multiple tuned mass dampers for attenuating undesirable oscillations of structures under the ground acceleration［J］.Earthquake Engineering and Structural Dynamics，2000，29(9):1405-1421.

［6］ 唐意，顾明.某超高层建筑TMD风振控制分析［J］.振动与冲击，2006，25(1):16-19. Tang Yi，Gu Ming.Analysis on control of wind induced vibration of a super-tall building with TMD［J］.Journal of Vibration and Shock，2006，25(1):16-19.

［7］ 谢壮宁.风致复杂结构随机振动分析的一种快速算法——谐波激励法［J］.应用力学学报，2007，24(2): 263-266. Xie Zhuang-ning.New rapid algorithm for wind-induced random vibration of complex structures［J］.Chinese Jour-nal of Applied Mechanics，2007，24(2):263-266.

［8］ 李小康，谢壮宁.大跨度屋盖结构风振响应和等效静风荷载的快速算法和应用［J］.土木工程学报，2010，43(7):29-36. Li Xiao-kang，Xie Zhuang-ning.Efficient algorithm and application for the wind-induced response and equivalent static wind load of large-span roof structures［J］.China Civil Engineering Journal，2010，43(7):29-36.

［9］ 杨位钦，顾岚.时间序列分析与动态数据建模［M］.北京:北京理工大学出版社，1988.

［10］ 谢壮宁，石碧青，倪振华，等.深圳京基金融中心气动抗风措施试验研究［J］.建筑结构学报，2010，31 (10):1-7. Xie Zhuang-ning，Shi Bi-qing，Ni Zhen-hua，et al.Experimental study on reduction of wind loads on Shenzhen Kingkey Financial Tower by aerodynamic strategy［J］. Journal of Building Structures，2010，31(10):1-7.

［11］ GB 50010—2010，高层建筑混凝土结构技术规程［S］.