带回流线的全并联直供系统研究

杜 川，黄彦全，谭红岩

0 引言

随着国民经济和对外贸易不断扩大，对铁路运量的要求也持续提高，载运量的不断增加和列车运行速度的提高使牵引网负荷电流和网络损耗增大，同时也使部分既有线供电臂末端电压水平过低，影响电力机车的正常运行和铁路运输的经济性[1]。

提高电气化铁路运能这一问题可以从两方面入手：一方面大力发展运载能力强的高速铁路，另一方面则对既有线路进行扩能改造[2]。目前国内的高速铁路主要采用AT 供电方式[3]。该方式具有供电质量高，牵引网阻抗小，供电距离长等优点，但也存在牵引变电所设施较多、土建工程较大的不足[4]。直接供电方式在国内电气化铁路中得到广泛应用，寻找一种投资少、效率高的全并联直接供电方式是具有很高使用价值的研究课题。本文在参考已有全并联AT 供电方式的基础上，对带回流线的全并联直接供电方式的电流分布、电压损失以及全并联方案进行分析。

1 带回流线的全并联直供牵引网络

不失一般性，以图1 所示带回流线的复线全并联直供牵引网电流分布作为后续的分析模型。假设钢轨对地漏导为零，忽略导线的分布电容以及横向连接线的阻抗，并认为所有导体都为均质导体且对地绝缘[5]。简化后的全并联直接供电牵引网等值电路模型如图2 所示。

图1 带回流线的复线全并联直供牵引网电流分布示意图

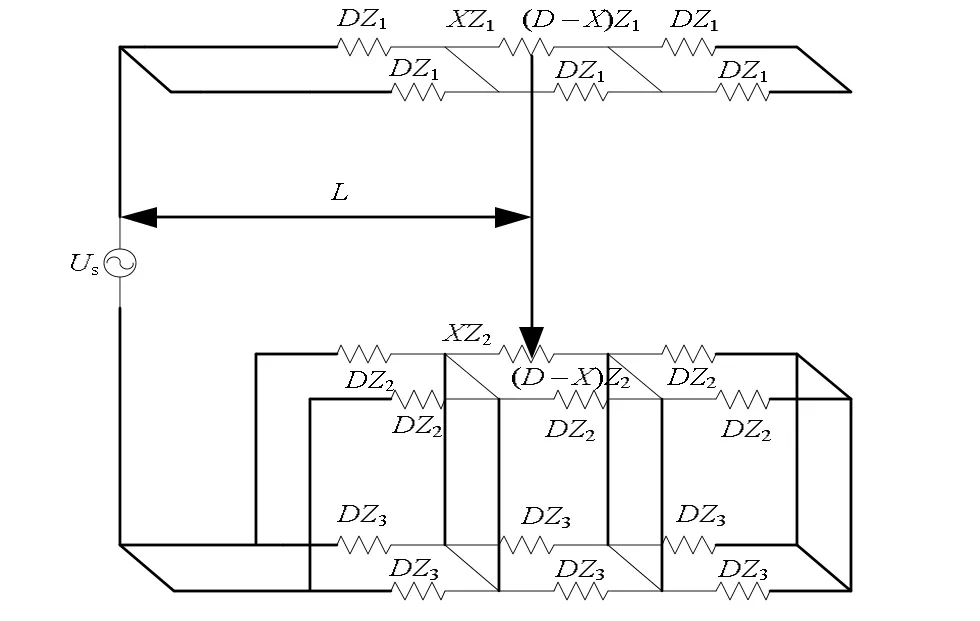
图2 带回流线的复线全并联直供牵引网等值电路图

1.1 带回流线的全并联直供牵引网电流分配

带回流线的全并联直接供电系统牵引网各电流分布如图1 所示，上行和下行的接触线、钢轨、回流线分别形成3 个闭合回路，其回路电压方程可表示为

对机车受流点和回流节点可以列以下方程：

根据并联区末端广义节点，列节点电流方程：

对下行牵引网可列网孔电压方程：

当机车取流I 为已知时，可由式（1）、式（2）、式（3）、式（4）得到电流分布模型如下：

式中，Z1、Z2、Z3分别为接触线、钢轨、回流线消去互阻抗后的等值单位阻抗；D 为单个并联区间的长度；X 为机车取流点与前一个全并联点的距离。

1.2 带回流线的全并联直供牵引网电压损失

当机车运行在如图2 所示位置时，将机车负荷看成一个电流源，则牵引网等值电路如图3 所示[6]。

对电路进行化简可以得到牵引网阻抗为

当供电臂内只有1 列车运行时，该列车对牵引网造成的压损为

图3 牵引网等值电路图

假设每一并联区间内都有1 列车取流，由于上下行都是通过连接线并联起来的，因此同列机车无论是在上行还是下行，都可视为在同一位置取流，对牵引网造成的电压损失也就相同[7]。

设2 列机车在同一供电臂取流，分别表示为A机车和B 机车，取流值为I1、I2。A 车到牵引变电所的距离为L1，距前一个并联点的距离为X1；B车到牵引变电所的距离为L2，距前一个并联点的距离为X2，且A 车比B 车更靠近变电所。

当2 列机车不在同一个全并联区间内，则A车取流对B 车取流点造成的压损为

B 车取流对A 车取流点造成的压损为

不失一般性，假设第K 列车取流为Ik，则其自身取流造成的压损为

第I 车取流对K 车取流点造成的压损为

由此可以得到一个一般性结论，当供电臂内有N 列机车取流时，任意一列机车M 取流点的牵引网电压损失为

显然牵引网电压最低点出现在供电臂最远处机车取流点，且最低电压值与负荷取流分布以及全并联次数有关。下面通过仿真做进一步分析。

2 仿真分析

本文利用Matlab/Simulink 仿真软件，结合实际牵引网供电系统进行仿真。假设供电臂长度为24 km；选择交直交机车作为负荷模型，其单车功率为5 MV·A，功率因数0.97；牵引网模型采用级联的方式，其参数如表1 所示。

表1 牵引网参数一览表

设上行最多分别有3 列机车取流，距牵引变电所分别为8，16，24 km；下行机车负荷与上行完全相同。对上下行分开供电、首末端并联供电和全并联供电3 种不同的供电方式以及不同的上下行负荷分布进行仿真计算，所得结果如表2 所示。

表2 不同供电方式下牵引网最大电压降一览表

对比分析表2 仿真结果可以看出：如果上下行负荷完全相同，则3 种工况下的牵引网最大压降相同；随着上下行负荷分布的不同，全并联供电方式对牵引网最大压降的减少明显优于另2 种方式，并且当上下行负荷分布越不相同，全并联供电对牵引网电压的改善越明显。

当仅上行有机车取流而下行无机车取流时，对并联点数量的不同进行仿真，可以得到仿真曲线图4。由图4 看出：牵引网最低电压与并联点数量有直接的关系，一般情况下，并联点数量越多，越能改善牵引网电压水平，但是并联点数量过多时，牵引网压损改善趋势迅速减小。从仿真结果来看，并联点数量一般取该供电臂最大负荷数量为最佳。

当上行只有1 列机车取流时，对机车负荷位置以及并联点位置的不同进行仿真，可以得到仿真曲线图5。由图5 可以看出：全并联对牵引网电压损失的改善是随负荷取流点变化以及并联点位置的变化而变化的，并且当并联点位置与负荷取流点恰好重合时，对牵引网压损的改善效果最佳，并联点位置与负荷取流点距离越远，其效果越差。

图4 上行有不同负荷时牵引网最低电压与并联点数量曲线图

图5 上行有不同单车负荷时并联点位置与牵引网最低电压关系曲线

3 结束语

本文从理论上分析了带回流线的全并联直供式系统电流分布以及牵引网电压损失，仿真验证了全并联对降低牵引网压损的有效性，并从仿真结果出发，定性得出并联点次数与牵引网压损的变化趋势，并联点位置的选择与牵引网最低电压之间的关系，为直供式系统的全并联方案选择提供了参考。

[1] 曹建猷.电气化铁道供电系统[M].中国铁道出版社，1993.

[2] 王进.高速铁路牵引供电调度仿真系统的牵引变电所仿真与实现[D].西南交通大学研究生学位论文，2004.

[3] 李群湛，贺建闵.牵引供电系统分析[M].西南交通大学出版社，2006.

[4] 邓云川.关于山区电气化铁道牵引供电系统问题的讨论[J].电气化铁道，2004，2 万公里论文集：188-191.

[5] 喻奇，吴江涛.客运专线牵引供电系统电气特性的仿真研究[J].电气化铁道，2010，（5）：11-13.

[6] 王猛.AT 所全并联供电方式牵引网电压损失分析[J].电铁信息网讯，2007，（2）：86-93.

[7] 邢晓乾.带加强导线的全并联直接供电技术的研究[D].西南交通大学研究生学位论文，2011.