基于CAFE的铝双辊连续铸轧凝固微观组织

陈守东， 陈敬超， 黄 攀， 吕连灏， 王 鹏， 彭 平

(1.昆明理工大学稀贵及有色金属先进材料教育部重点实验室云南省新材料制备与加工重点实验室，昆明650093;2.昆明理工大学材料科学与工程学院，昆明650093)

凝固过程对液态金属成型有重要的影响［1，2］。凝固过程直接决定金属的微观组织，而微观组织又对材料的性能起到重要的作用和影响。研究凝固过程主要是通过控制各种工艺参数和凝固参数(如温度梯度、浇注温度、铸轧速率、形核过冷度等)以达到控制凝固微观组织形成的过程，进而提高材料的各种综合性能。采用铸轧实验观察和测量不同铸轧工艺条件下铸轧出的板带材金相组织来研究铸轧工艺参数对凝固微观组织形成及演变的影响规律，则需要大量的人力、物力和时间。随着计算机模拟技术和模拟凝固数学模型的发展，这种耦合的数学模型可以时时更新凝固材料因温度等外界条件而变化的物性参数，而实现对凝固过程逼真的模拟。采用数值模拟研究凝固过程不仅高效和经济，而且可以有效方便地预测工艺参数和凝固参数变化对凝固微观组织的影响。通过模拟可以减少连续铸轧凝固过程的缺陷和优化凝固微观组织，达到提高最终产品质量的目的。

铝双辊连续铸轧是一种全新的薄板带材生产工艺［3］，液态金属可以不经过热轧直接铸轧生产出薄板带材。它将连续铸造和热轧有机地结合起来，一方面可以实现连续冷却和凝固，另一方面可以提高材料的塑性成型能力。双辊薄带连铸技术是冶金及材料领域的一项前沿技术，其特点为:简化生产工序，缩短生产周期，减少设备投资，降低生产成本，具有巨大的技术和经济潜力。

随着计算机仿真技术的不断发展，开发出多种模拟凝固微观组织的数学模型，主要有:确定性模型、随机性模型和相场法［4］。确定性方法可以把凝固过程中的物质守恒方程和形核长大模型很好地耦合在一起，因考虑了宏观偏析和固态传输而更接近实际的凝固过程。确定性法未考虑晶粒生长过程中的一些随机现象，如形核随机分布、随机晶体取向等而无法模拟预测凝固过程中枝晶的生长和形貌［5～7］。相场法采用统一的控制方程，不区分固液相、固液界面及跟踪固液界面［8～15］，模拟晶粒三维长大有其独特优势，但是计算量大，计算效率低，不能准确模拟双辊连续铸轧的凝固过程。随机性方法可以将能量方程与形核长大耦合起来，更适合模拟预测柱状晶的形成以及柱状晶向等轴晶的转变过程，主要有蒙特卡罗法和元胞自动机法。MC法基于能量最小原理计算晶粒生长概率，缺乏对晶粒生长物理机制的考虑，没有明确的物理背景，无法实现定量模拟。CA法数值计算处理方便，容易和各种物理过程结合。模拟时，宏观温度场与微观形核生长模型耦合在一起，CA模型可以与有限元方法结合起来计算温度场和凝固微观组织;采用随机方法建立形核模型，采用枝晶尖端生长动力学建立晶粒长大模型;采用双重网格划分:宏观温度场的计算采用较粗的网格，微观的晶粒长大则采用细的网格;CA法具有较强物理基础，主要用于模拟晶粒生长的竞争机制、晶粒结构以及形态的演变过程［16～22］。

本研究采用CAFE法对双辊连续铸轧纯铝凝固微观组织进行了模拟，同时研究了铸轧工艺参数和金属凝固参数对凝固微观组织的影响规律。

1 数学模型

1.1 控制方程［23］

(1)质量守恒方程

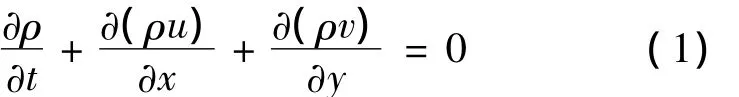
(2)动量守恒方程

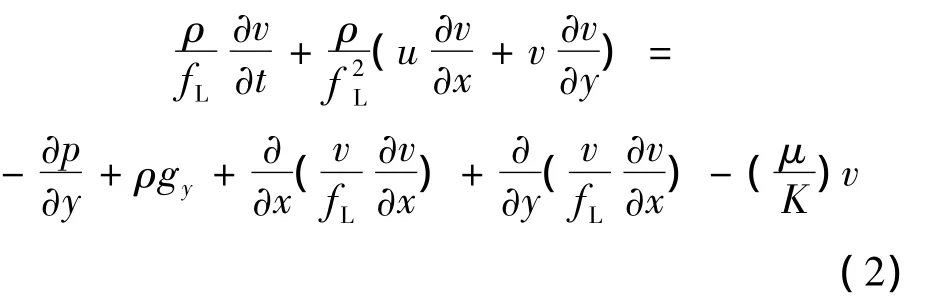
(3)能量守恒方程

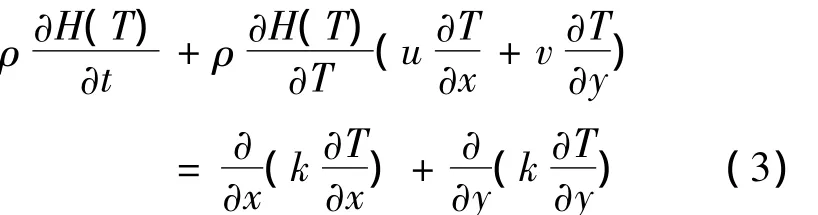
其中，

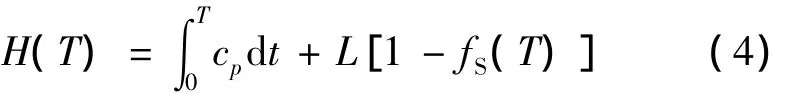
式中:u，v分别为x和y方向上的速率分量，m·s-1; fL为液相率;fS为固相率;p为压力，Pa;gy为y方向上重力分量，m·s-2;ρ为密度，kg·m-3;μ为绝对黏度，Pa·s;k为热传导率，W·m-1·℃-1;K为渗透率，m2;cp为比热容，J·kg-1·K-1;t为时间，s;L为凝固潜热，J·kg-1;T为节点温度，℃;H为焓，J·mol-1。

1.2 形核模型

鉴于双辊薄带连续铸轧金属凝固的特点，考虑到形核过冷度的影响和形核的连续性以及液相流动等因素的影响，采用Rappaz等［4］提出的基于高斯分布的异质形核模型描述双辊薄带连铸凝固过程中柱状晶前沿液相中等轴晶形核密度随过冷度的变化规律。双辊薄带连铸凝固过程中柱状晶前沿液相中等轴晶粒随过冷度的增大而增加的晶粒密度可由连续形核分布公式dn/d(ΔT)来描述。基于高斯分布的连续形核模型为

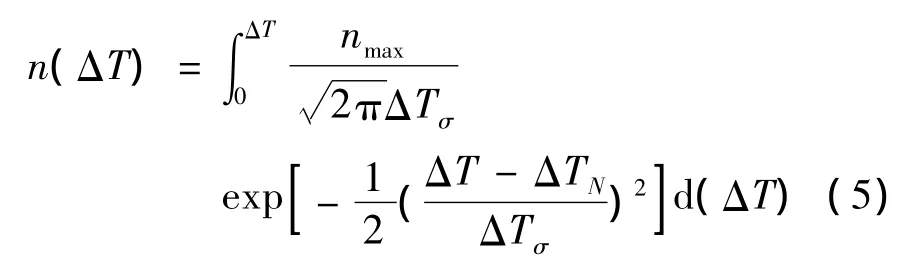
式中:n(ΔT)为过冷度ΔT下的形核密度;nmax是总的初始潜在形核质点密度;ΔTN，ΔTσ分别为形核过冷度的平均值和方差，可由差热分析(DTA)实验确定。双辊表面形核和液相内部体积形核分别采用两种不同的形核分布函数来处理，形核模型的建立主要是为了计算形核密度n(t)。

1.3 枝晶尖端生长动力学模型

晶粒长大不仅与枝晶尖端稳定生长有关，而且也和连续形核过程及非稳态的枝晶结构有密切的关系。凝固过程中液/固界面沿着最大散热方向向垂直界面前沿移动的速率为v时，液/固界面前沿中温度和溶质分布方程如下:

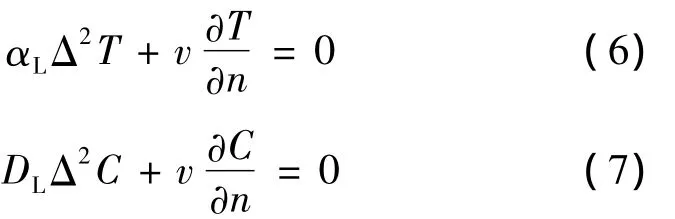
式中:T为合金温度;C为合金的浓度;DL为液相原子的扩散系数;αL为传热系数。通过上述公式并不能获得枝晶尖端生长速率v和枝晶尖端生长半径R，LANGER等［24］对该方程进行了改进，引入R=λC作为稳定界面理论的限制条件，其中λC为最小标准扰动波长。

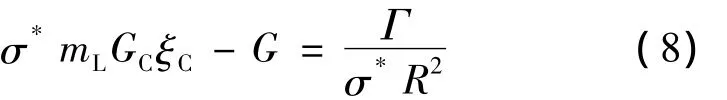
式中:mL为液相线斜率;GC为枝晶尖端液相溶质浓度梯度;ξC为溶质浓度的贝克利系数函数;G为温度梯度;σ*为定系数，σ*=1/(4π2);Γ为Gibbs-Thompson系数;R为枝晶尖端半径。

立方晶系金属晶体的择优生长方向为［100］，枝晶尖端生长模型采用KGT模型［21］。在KGT模型中过冷度由四个部分组织。

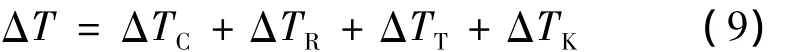
式中:ΔT为枝晶尖端过冷度;ΔTC为成分过冷度; ΔTR为曲率过冷度;ΔTT枝晶尖端动力学过冷度; ΔTK为溶质扩散过冷度。

鉴于双辊连续铸轧是亚快速凝固过程，此过程相对于快速凝固过程的枝晶生长速率不是很高。因生长动力学系数很大，枝晶尖端生长动力学过冷度可以忽略。此外，由于凝固在准平衡状态下进行，可以认为合金的平衡分配系数、液相中溶质的扩散系数保持不变。因此可对KGT模型进行修正，修正后的KGT模型如下:

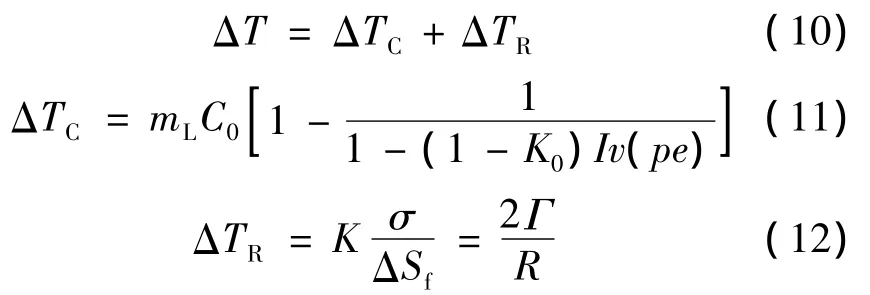
式中:C0为合金初始质量浓度;K0溶质平衡分配系数;σ为界面能;ΔSf为溶液体积熵;Pe为溶质浓度的贝克利系数;Iv(pe)为pe的伊万卓夫函数。

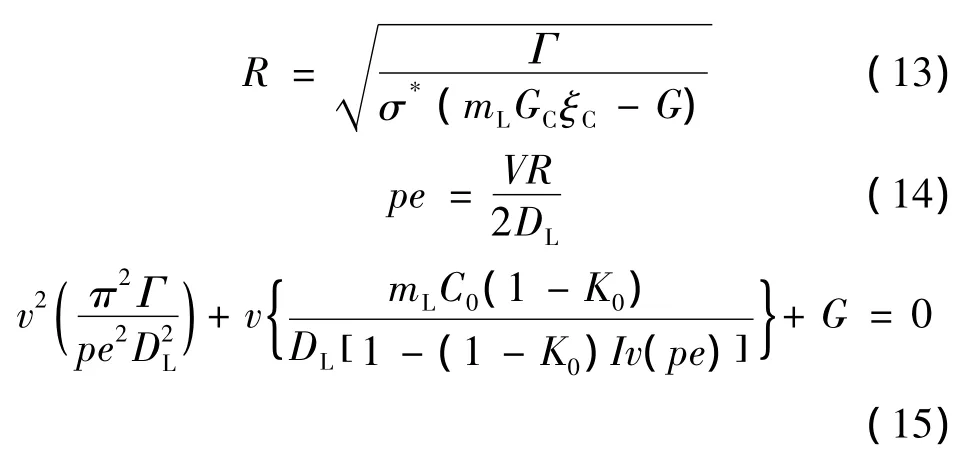
通过上述公式求解可以获得枝晶生长速率v和枝晶尖端半径R，故可以采用修正的KGT模型来描述枝晶生长过程。

2 数值模拟

2.1 计算模型

双辊连续铸轧纯铝工艺示意图如图1所示［25］。因采用水平式同径双辊铸机进行模拟实验，注水口的宽度几乎等于铸辊的宽度，同时采用侧封板绝热和加热装置后，可以将双辊薄带连铸过程的模拟简化为二维问题。从连续铸轧示意图可知，铸轧区域是对称分布的，为了减少有限元计算量，只需要计算对称面的一半即可。应用元胞自动机模型模拟连续铸轧过程，采用有限元法计算宏观温度场，凝固组织模拟要与有限元法相耦合。一个简单的有限元网格模型如图2所示。有限元网格被分割为m×n个网格，网格中的每个节点的坐标为(i，j)，当元胞状态是液态时被赋予0，当元胞状态是固态时被赋予1，当元胞状态是液固态之间时被赋予(0，1)。

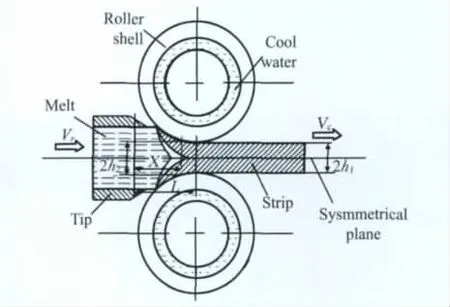
图1 铝双辊连续铸轧示意图Fig.1 Schematic diagram of aluminum twin-roll casting

图2 计算元胞模型Fig.2 Calculation method of capturing cells

随着金属凝固过程的进行，固相率ΔfS(i，j)不断发生变化。利用二维m×n网格来表示每个元胞的固相率fS(i，j)和固相率增量ΔfS(i，j)。随着凝固微观组织的形成，各个元胞的固相率在逐渐增加，当元胞的固相率fS(i，j)≥1时，液相将转化为固相。凝固组织的形成和凝固动力学演变可以通过元胞状态的改变来获得。当网格节点(i，j)和(a，h+r)之间的距离满足下式时，节点(i，j)可以作为计算区域的节点。

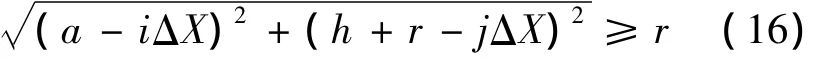
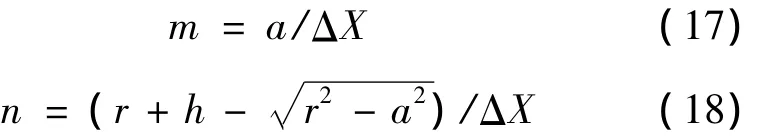
根据上述方程，只要网格数量m×n确定，如输入a，r和h等参数到操作程序中就可以再显双辊连续铸轧薄带凝固微观组织演变过程和晶粒大小及分布。

2.2 边界条件

(1)入口

传热:T=T0(T0为浇注温度)

流动:u=0;v=v0(v0为水口流速的y方向的分量)

(2)出口

传热:∂T/∂y=0

流动:u=0，v=vcast(vcast为铸轧薄带拉速)

(3)熔池表面

面板数据模型一般有三种情形：混合模型、个体固定效应模型和随机效果模型。对于三种模型的选择可以用F统计检验和Hausman统计检验来进行筛选。F检验结果显示，混合回归模型要优于个体固定效应回归模型，而Hausman检验结果显示，个体固定效应回归模型要优于个体随机效应回归模型。因此实证最终结果选择混合回归模型。即如下模型：

传热:∂T/∂y=0

流动:v=0

(4)熔池中心对称面

传热:∂T/∂x=0

流动:u=0

(5)铸轧辊与熔体接触面

传热:冷却铸轧辊与熔体接触的界面采用等效传热理论处理，即

式中，T为熔体温度，℃;Tf为铸轧辊中冷却水温度，℃;hi为换热系数，W·(m·℃)-1。

流动:与铸轧辊接触的弧形固相传输采用模拟软件中的C语言用户函数处理。

3 模拟结果及分析

使用计算机语言对凝固过程进行编程，利用该软件可以模拟双辊连续铸轧纯铝凝固微观组织的再显和后处理显示。计算过程中每个时间步长都计算凝固过程中的形核和枝晶尖端生长动力学。通过调试程序可以节省大量计算时间。

具体模拟条件:水平式铸轧机，铸轧速率:1010～1060mm/min;辊径:850mm;浇注温度:690～695℃;轧出坯料厚度5.9～6.1mm，宽度1.2m;铸嘴厚度4～5mm，宽度1.0m;铸坯速率比铸辊速率快100mm/min;铸轧区长度40～80mm。采用合金钢辊套。计算区域被分割为1.050×107个元胞，元胞尺寸为1μm×1μm×1μm。

基于计算机程序对双辊连续铸轧纯铝薄带不同铸轧速率下的凝固微观组织进行了模拟，其模拟结果如图3、图4所示。

图3 不同铸轧速率下铸轧区纵向模拟凝固微观组织(a)铸轧速率为0.8m/min;(b)铸轧速率为1.0m/min;(c)铸轧速率为1.2m/minFig.3 The solidification structure on the lengthwise section with different casting speed (a)0.8m/min; (b)1.0m/min;(c)1.2m/min

图4 不同铸轧速率下铸轧区横向模拟凝固微观组织 (a)铸轧速率为0.8m/min; (b)铸轧速率为1.0m/min;(c)铸轧速率为1.2m/minFig.4 The solidification structure on the crosswise section with different casting speed (a)0.8m/min;(b)1.0m/min;(c)1.2m/min

从模拟结果可以看出，在靠近辊面处出现了一层很薄的细小等轴晶区，位向杂乱排列无方向性。随着凝固的进行，这些晶粒发生长大，晶粒数目在减少，晶粒尺寸在增大，各个晶粒的位向趋于一致。在金属凝固过程中，枝晶的生长具有择优取向。只有那些与温度梯度方向一致的晶粒才会长大，而其他偏离温度梯度方向的晶粒则会在生长过程中被择优取向的晶粒所吞并。在双辊连续铸轧凝固过程中，垂直辊面方向上的温度梯度最大，散热最快，即垂直于铸轧辊辊面的晶粒生长速率最大，由于晶粒间的竞争生长机制，使他们快速地长到了其他晶粒的最前方，吞并其他偏离辊面垂直方向的晶粒，进而长大形成柱状晶。在柱状晶生长过程中，当其前沿的液体区域过冷度达到一定时，可在柱状晶前沿出现大量的形核质点，随着凝固的进行形核质点长大，形成等轴晶阻碍柱状晶的继续长大，从而发生柱状晶向等轴晶的转变。

从模拟结果可知，在低的铸轧速率下，由于铸轧区和铸轧辊的接触时间长，对流换热系数大，因此铸轧辊表面形成的表层细晶区很薄且不是很明显，但是形成的晶粒很细小。随着铸轧速率的增加，铸轧区和铸辊的换热系数变小，表层的细晶区增厚且晶粒尺寸增大。随着铸轧速率的增大，等轴晶的比例有所增大，这与铸轧速率增大时，模型的流场发生紊乱有关，产生了很多的异质形核的基底，易于等轴晶的形成。低的铸轧速率下可能产生粗大的柱状晶和等轴晶，随着铸轧速率的增大，凝固晶粒组织变得均匀，晶粒尺寸变小。

4 实验验证

以工业纯铝为研究对象，采用水平式同径双辊铸机进行实验验证，注水口的宽度几乎等于铸辊的宽度，同时采用侧封板绝热和加热装置，可以将双辊薄带连铸过程的模拟简化为二维问题。同时和相同条件下的实验结果进行比较，以验证所建立的微观数学模型的可靠性。在浇注温度为695℃、铸轧速率1.0m/min、熔池高度40mm时的实验铸轧生产出的纯铝薄带凝固组织如图5所示。

对比模拟结果和实验结果可以看出，无论从晶粒形貌、表层细晶区和柱状晶区域的大小，还是柱状晶向等轴晶的转变来看，模拟结果都很好地与实验结果吻合。从模拟和实验结果还能看出，凝固过程中并没有得到穿晶组织，薄带中心区域有等轴晶的出现，这主要是由于模型底部的换热系数很大(与铸轧辊辊面的换热量大的缘故)，降低了中心熔体的温度梯度，使中心熔体的过冷区域和过冷度都增大，阻碍柱状晶的继续长大，有利于形成中心等轴晶。

图5 浇注温度为695℃、铸轧速率1.0m/min、熔池高度40mm时的实验条件下啮合点前铸轧纯铝薄带凝固组织 (a)横向凝固组织;(b)纵向凝固组织Fig.5 Solidification structure in front of nip point on the cross section and lengthwise section of twin-roll continuous casting aluminum thin strip produced under the pouring temperature 695℃，casting velocity 1.0m/min，molten pool height 40mm (a)grain microstructure at the crosswise section; (b)grain microstructure at the lengthwise section

5 结论

(1)应用基于连续性异质形核模型和修正的枝晶尖端生长动力学模型KGT的元胞自动机模型，对双辊连续铸轧纯铝凝固微观组织进行了模拟，模拟结果显示，此模型可以很好地显示出凝固过程中的固相、液相以及固液界面，解释和预测啮合点前柱状晶和等轴晶之间的转化和晶粒尺寸大小。模型显示，柱状晶主要分布在靠近铸轧辊面附近，等轴晶则是远离铸轧辊面而靠近薄带的中心区域。

(2)对不同铸轧速率下双辊连续铸轧生产纯铝薄带的凝固微观组织进行了模拟，通过模拟和实验结果的对比，可以很好地解释和预测凝固过程中的各种凝固缺陷，如枝晶偏析、凝固缩孔等。

(3)不同铸轧工艺参数对双辊连续铸轧纯铝的凝固组织影响进行了模拟，在低的铸轧速率、对流换热系数大时，铸轧辊表面形成的表层细晶区很薄且不是很明显，但是形成的晶粒很细小。随着铸轧速率的增加和铸轧区和铸辊的换热系数变小，表层的细晶区增厚且晶粒尺寸增大，等轴晶的比例有所增大，易于等轴晶的生成。铸轧速率较小时可能产生粗大的柱状晶和等轴晶，随着铸轧速率的增大，凝固晶粒组织变得均匀，晶粒尺寸变小。

［1］BOETTINGER W J，CORIELL S R，GREER A L.Solidification microstructures:Recent developments，future directions［J］.Acta Mater，2000，48:43-70.

［2］许庆彦，冯伟明，柳百成，等.铝合金枝晶生长的数值模拟［J］.金属学报，2002，38(8):799-803. (XU Y Q，FENG W M，LIU B C，et al.Numerical simulation of dendrite growth of aluminum alloy［J］.Acta Metallurgica Sicina，2002，38(8):799-803.)

［3］BAE J W，KANG C G，KANG S B.Mathematical model for the twin roll type strip continuous casting of magnesium alloy considering thermal flow phenomena［J］.Journal of Materials Processing Technology，2007，191(1/2/3):251 -255.

［4］PAPPAZ M，GANDIN C A.Probabilistic modelling of microstructure formation in solidification processes［J］.Acta Metallurgica et Materialia，1993，41(2):345-360.

［5］WANG Y C，BECKRMANN C.Multi-scale-phase modeling of dendrite alloy solidification，transport phenomena in solidification［J］.ASME Heat Transfer Division，1994，284: 75-95.

［6］BROWN D J，HUNT J D.A model of columnar growth using a front-tracking technique［C］//Modeling of Casting，Welding and Advanced Solidification Processes XI. Aachen，Germany，2000:437-444.

［7］马长文，沈厚发，黄天佑，等.等轴晶移动对宏观偏析影响的数值模拟［J］.材料研究学报，2004，18(3):232-238. (MA C W，SHEN H F，HUANG T Y，et al.Numerical simulation of macro-segregation with equiaxed grains movement［J］.Chinese Journal of Materials Research，2004，18 (3):232-238.)

［8］ZHANG G Y，JING T，LIU B C.Microstructure simulation of aluminum alloy casting using phase field method［J］.Int J Cast Metal Res，2002，15(13):237-240.

［9］ZHU C S，WANG Z P，JING T，et al.Phase-field simulation of dendrite sidebranching induced by thermal noise［J］.Trans Nonferrous Met Soc China，2004，14(6):1106 -1110.

［10］GUO J J，LI X Z，SU Y Q.Phase field simulation of structure evolution at high growth velocities during directional solidification of 55%Ti-45%Al alloy［J］.Intermetallics，2005，13:275-279.

［11］朱耀产，杨根仓，王锦程，等.二元共晶定向凝固的多相场法数值模拟［J］.中国有色金属学报，2005，15(7): 1026-1032. (ZHU Y C，YANG G C，WANG J C，et al.Multi-phase field simulation of unidirectional solidification for binary eutectic alloys［J］.The Chinese Journal of Nonferrous Metals，2005，15(7):1026-1032.)

［12］LI X Z，GUO J J，SU Y Q，et al.Phase-field simulation of dendrite growth for binary alloys with complicate solution models［J］.Trans Nonferrous Met Soc China，2005，15 (4):769-776.

［13］赵红兆，荆涛，柳百成.铝合金三维枝晶生长相场模拟［J］.金属学报，2005，41(5):491-495. (ZHAO H M，JING T，LIU B C.Simulation of 3-D dendrite growth of aluminum alloy by phase field model［J］. Acta Metallurgica Sicina，2005，41(5):491-495.)

［14］李梅娥，杨根仓，周尧和.二元合金高速定向凝固过程的相场法数值模拟［J］.物理学报，2005，54(1):454 -459. (LI M E，YANG G C，ZHOU R H.Phase field modeling of directional solidification of a binary alloy at high velocities［J］.Acta Physica Sinica，2005，54(1):454-459.)

［15］杨玉娟，王锦程，朱耀产，等.自由共晶生长的多相场等温数值模拟［J］.稀有金属材料与工程，2007，36(4): 573-577. (YANG Y J，WANG J C，ZHU Y C，et al.Multi-phase field simulation of isothermal free binary eutectic growth［J］.Rare Metal Materials and Engineering，2007，36(4): 573-577.)

［16］BELTERAN-SANCHEZ L，STEFANESCU D M.A quantitative dendrite growth model and analysis of stability concepts［J］.Metall Mater Trans(A)，2004，35(8):2471-2485.

［17］ZHU M F，LEE S Y，HONG C P.Modified cellular automaton model for the prediction of dendrite growth with melt convection［J］.Phys Rev E，2004，69(61):061610-1-061610-12.

［18］XU Q Y，FENG W M，LIU B C.Coupled macro-micro modeling for prediction of grain structure of Al alloy［J］. Trans Nonferrous Met Soc China，2004，14(1):71-77.

［19］康秀红，杜强，李殿中，等.用元胞自动机与宏观传输模型耦合方法模拟凝固组织［J］.金属学报，2004，40 (5):452-456. (KANG X H，DU Q，LI D Z，et al.Modeling of the solidification microstructure evolution by coupling cellular automaton with macro-transport model［J］.Acta Metallurgica Sicina，2004，40(5):452-456.)

［20］陈晋，朱鸣芳，孙国雄.用CA方法模拟过冷熔体中自由树枝晶的生长［J］.金属学报，2005，41(5):799-803. (CHEN J，ZHU M F，SUN G X.Numerical simulation on free dendrite growth in undercooled melt using cellular automaton method［J］.Acta Metallurgica Sicina，2005，41 (5):799-803.)

［21］王狂飞，李邦盛，米国发，等.Ti44Al合金胞/枝晶转变及其生长过程的数值模拟［J］.金属学报，2007，43 (2):211-216. (WANG K F，LI B C，MI G F，et al.Numerical simulation of cellular/dendrite transition and its growth during directional solidification of Ti44Al alloy［J］.Acta Metallurgica Sicina，2007，43(2):211-216.)

［22］LIU X B，XU Q Y，JING T，et al.Research on microstructure of aluminum twin-roll casting based on cellular automation［J］.Trans Nonferrous Met Soc China，2008，18 (4):944-948.

［23］胡汉起.金属凝固原理［M］.北京:机械工业出版社，1991.

［24］LANGER J S，MULLER-KRUMBNAAR H.Stability effects in dendrite crystal growth［J］.Journal of Crystal Growth，1977，42:11-14.

［25］LIU X B，XU Q Y，JING T，et al.Simulation of microstructures in solidification of aluminum twin-roll casting based on CA［J］.Trans Nonferrous Met Soc China，2009，19(2):422-427.