信息量与时间的数理通路——信息元胞方程

郭 仪，杨华磊，付海东

(兰州大学经济学院，兰州730000)

从香农创立信息论到维纳对信息的发展，对于信息的研究一直处于活跃阶段.有的着眼信息的扩散，进而寻找信息扩散方程［1－3］;有的着眼对信息本质的界定，即信息是什么［4－7］，进而给出其概念的文字陈述或数理定义;有的研究信息量的测度或者信息在那个层次上其量是守恒的［8］，进而给出一个通项公式和研究面;有的从信息的角度思考社会和自然现象［9］，或者在研究信息以及其他相关问题时派生新的信息问题，如信息熵［10］在各领域中的应用.但一个体或一群体的信息水平随时间的增加，其如何发生改变.是在记忆中累增，还是在遗忘中间歇?其增速是单调，还是震荡?这既是信息科学的范畴，也是认知科学研究的区域，但对这一边缘交叉问题的探究，好像被人所忽视.其涉及着信息科学的一些基础问题，当然包括什么是信息，信息如何扩散等;也涉及认知科学中一系列法则，如遗忘和记忆.为回答上述提出的问题，即寻找一个方程(信息元胞方程)去模拟跟踪考察对象任一时点上的信息水平，行文遵从下述布局.

先引入反映考察主体信息水平分布的信息元胞矩阵，并用矩阵的模去表征考察主体所拥有的绝对信息元胞量，即信息水平;同时给出在活动空间上考察主体在与其他主体在接触过程中所遵从的认知法则.为单纯的考虑考察对象和活动空间的作用，设定“总信息元胞量一直不变，没有第三方和新维度信息创造源给考察对象以新信息元胞，没有划分不完备引致的信息挖掘现象”等一系列假设.根据上述设定，得出“活动空间内信息元胞量一直大于或者等于考察对象的信息元胞量”的命题，并且引出的“下一点上信息的增量与‘活动空间的信息总量与此刻其所拥有的信息量之差’成正比”的认知推论.再通过考察信息性质以及信息量的多寡，依此建立符合逻辑的离散和连续两种认知模型，进而给出考察主体任一时点上所拥有的信息元胞量函数，而此函数具有“只增不减，但增速放缓”的特性.上述的研究方法在某种程度上归为信息扩散的逆范畴，而研究的内容促进了认知科学和信息科学的融合.假设:

1)考察主体在面对逐渐增加的信息量，其主观上不存在自满;

2)考察个体对已获得的信息，不存在遗忘;考察个体对新接触的信息是均匀随机的记忆，同时记忆具有瞬时特性(考察主体对信息元胞获得所需要的时间，只局限两次接触之间的累计和，而信息元胞的传递，即接触本身在此假设不花费时间).

1 信息元胞矩阵

为寻找考察主体在任一时刻上其拥有的信息水平，先界定一些本文将要用到的概念.考察主体可以近似看作携带一定信息的人或者一个群体;而信息在量上的最小单元记住基本信息元胞，考察主体所携带的所有不同形式的信息元胞的总和记住考察主体的信息水平;信息元胞矩阵是用来表征考察主体所携带的信息元胞以及元胞分布;考察主体的活动空间可以近似看作其的最大交往圈;而其交往圈之外的人群可近似看作第三方因子;划分的不完备引致的信息挖掘，即划分过程中由于主观和客观条件的限制使得信息子集之间存在交集.

若采取横向标准把考察对象与其活动空间上的所有信息元胞化分为不存在交集的类，即信息空间是n维的，其用来衡量信息的宽度.若采取纵向标准再对所有信息进行划分，即把每个维度下的信息都分为若干个独立的信息分量，其用来衡量信息的深度，取横向维度下的纵向维数最大值记为L.若对于纵向维度采取特殊聚类，则总可以实现纵向和横向的一致性，即纵向的最大维数和横向的维数相同，进而生成一n维的信息空间.总之，在任一时点上，考察系统内的任一个体k所携带的信息元胞量可用一矩阵表示，称此矩阵为信息元胞矩阵

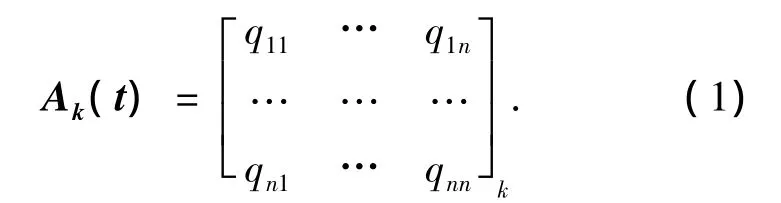
纵向维数的最大值L=n，矩阵中任一元素qij代表考察个体k在第i信息维度上的第j分量上所携带的信息元胞量.一般若考察主体k携带此位点上的信息元胞，则qij取1;若k不携带此位点上的信息元胞，则qij就取0;一般考察主体k通过自带或接触其他主体k携带某种信息元胞.并把考察主体所携带的总信息元胞量定义为信息元胞矩阵的测度，也即考察主体任一时点上的信息水平

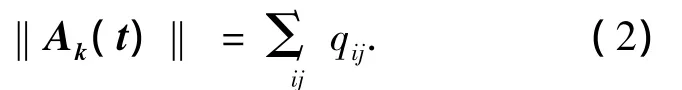
为简化问题分析方便，在此不妨设定信息空间的维度和活动空间上的总主体数均为n，在进一步的研究中，将逐渐讨论信息空间的维数与主体数不一致的情况.而行文只是对信息元胞方程在严格假设条件下进行的初步探讨，为进一步的研究工作提供参考，故对不一致下信息元胞方程的探究，将放在后续研究工作中.故设初始考察主体携带的信息元胞与其他主体携带的信息元胞在量上相同，但形式完全差异，在接触的过程中这种绝对差异性将保证信息交换的存在;又设考察对象内部不存在信息创造的机制和对活动空间以外空间传递来的新维度信息元胞是封闭的，即其信息元胞的增加只来自活动空间上.这保证了可以单纯的考虑考察对象与活动空间的作用，撇开任何第三方因子，就看考察对象“通过接触此空间上个体”获得的信息元胞量与时间的关系;再设初始信息元胞完全填满信息矩阵，活动空间内的信息元胞不存在表征为“遗忘事件”进而减少信息元胞的因子，这保证了活动空间内总信息元胞随时间不发生改变，包括量和形式上;此条件也使得每个个体初始刚好携带单位绝对差异的信息量.总之，活动空间上的总信息量不变，而每个个体初始的信息元胞矩阵是对维单位阵的任意交换两行生成的矩阵，此类矩阵的特性保证上述设定的信息特性和上述假设.

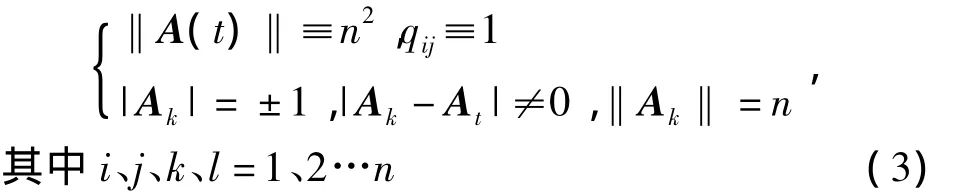
2 传递中的认知法则

为寻找考察个体在活动空间上信息水平与时间的关系，设定考察对象获得信息的方式是随机瞬时均匀的，这间接的反映考察个体的记忆质量和学习品质.均匀和随机说明考察对象的学习方式和记忆品质是统计意义上的平均值;瞬时说明接受信息不需要时间，在发生接触的瞬间两主体完成信息传递，通过获取信息而耗费的时间只体现在相邻两次接触之间的时间间隔.考察主体k与一主体l第一次接触后主体k获得的信息元胞数量X服从均匀分布，因初始每个个体携带的信息元胞数量为n，并且传递哪类信息元胞是随机的，故通过此次接触后考察主体获得的信息元胞数量的期望值

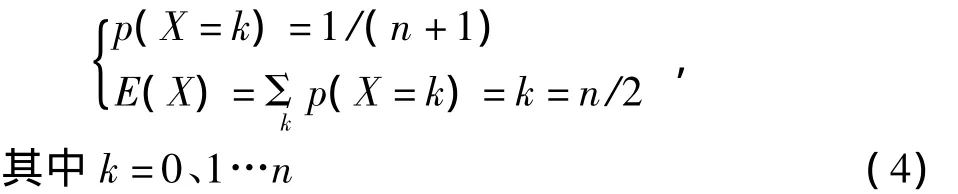
根据上述一系列设定，可以推出活动空间内总信息元胞量一直大于或者等于考察对象的信息元胞量命题，再根据此命题，进而可推出此时所遵从的认知法则:“考察对象下一点上的信息增量与‘活动空间上的信息总量与此刻考察主体所拥有的信息总量之差’成正比”，而由这个命题给出的信息水平的解，将具有“考察主体的信息元胞量逐渐增加，但单位时间内获得的信息元胞量趋于减少”性质.

前者源于在对已获得信息没有遗忘的认知假设下，考察主体获得的信息只会增加;后者可以有以下陈述加以说明，当主体k与主体l发生第2次接触时，因第1次接触后k已从l上平均获得n/2单位绝对差异的信息元胞，根据上述信息元胞传递的随机和均匀分布假设，此次将有n/4单位信息元胞传递.随时间变化，传递的信息元胞量将按照上述法则依次类推.

若把每单位时间所接触的个体数看做一个群体，则在统计意义上，此群体向后每次向考察主体所传递的信息元胞量，将趋于减少.图1将简单陈述在单位时间内如果接触的个体数一定，且单位时间内每个体被接触的可能性相同情况下，为什么在统计意义和认知法则上单位时间内所获得信息元胞量会逐渐减少.

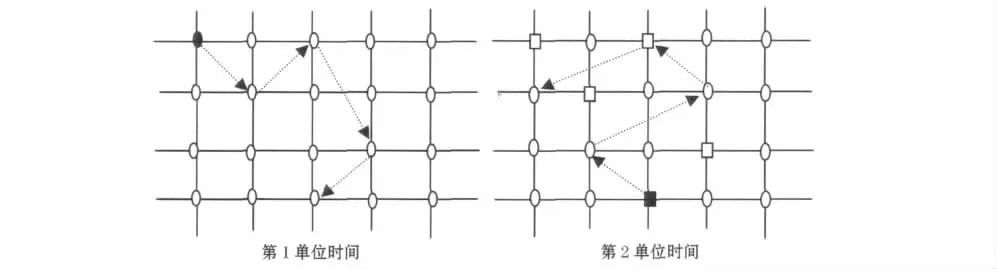
图1 单位时间内所获信息元胞

根据设定信息元胞总量和形式都不变，从第一单位时间接触开始，选取一考察个体，同时选取其获得信息元胞的初始的4个单位时间，观察此个体的行为路径，其所接触的个体在图2中标示.图2中的黑点代表此单位时间内考察主体运动的起点，也是相邻上单位时间内最后接触的个体.箭头代表行为路径，栅栏表示每个主体所处的位置;没有碰撞前的主体都用圆形表示，碰撞1次用方形表示，碰撞2次用菱形表示，碰撞3次用梯形表示;一般碰撞的次数越多，下次碰撞从其上获得信息量越少.

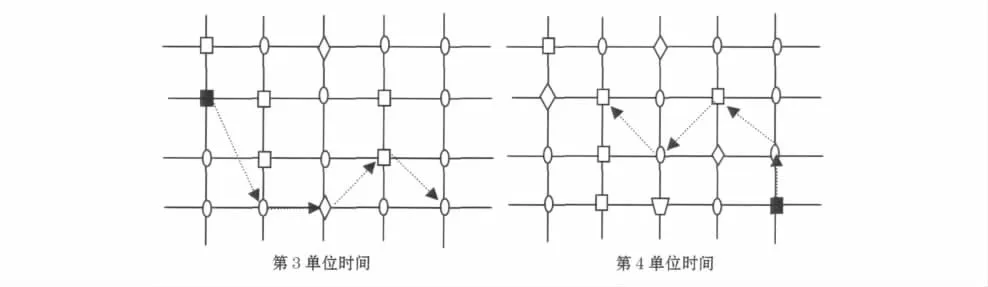
图2 单位时间内所获信息元胞

这种单位时间内获得信息元胞量递减认知法则，可通过在没洞的台球案上打台球进行类比，初始假设每个台球携带相同的信息量，但其形式完全不同.只要有碰撞就会有信息扩散，每一次打出母球后接触的台球个数，在统计意义上是相同的，且第k次接触同样一球从其上获得的信息量小于或者等于第k－1次接触它所获得的信息量.第1次打出母球后其吸收的信息假若为一个量，第2次母球打出后又存在一吸收的信息量，第2次吸收量在平均上小于或者等于第一次获得的，并且向后每一次接触后获得信息元胞量在统计意义上都小于或者等于前一次.这因为后来母球接触的台球有可能被上一次接触了，一旦接触后再次被接触就获得的信息量将减少，这由认知和统计法则决定.

3 信息元胞方程

根据以上设定，单位时间内考察主体获得的新信息元胞量随着时间逐渐减少，源于图2所示的认知法则.单位时间所获得信息元胞量取决于其单位时间内所接触主体数以及从每个主体上平均所获得信息元胞量，故减少的方式可表征为如下2种:一是单位时间内平均接触的主体数不变，但从每个接触个体上获得的绝对信息元胞数量逐渐减少;二是单位时间接触人数逐渐变少，但从每个接触个体上获得绝对信息元胞量不变.总之，随着时间变化，未来单位时域内考察个体获得绝对信息元胞数量减少.又因文章仅考察某时点上的状态结果，且上述2种方式在状态结果上是等价的，故在此先考虑后一种的信息元胞方程，即单位时间内接触的个体逐渐减少，但从每个主体上获得绝对信息元胞不变的情况，随后通过后者再去反演前者.

3.1 离散型的信息元胞方程

因存在基本的信息元胞，故信息扩散的真实情况应是离散的.根据上述设定和推理，单位时间内，考察主体所获得的信息元胞量逐渐减少，则其最终可归结为，在每接触一个体所获得的绝对信息元胞一定情况下，单位时间内接触的人数逐渐减少的命题.又根据统计和认知法则，单位时间内新增加的接触次数正比于总信息元胞量与此刻考察主体所拥有的元胞量之差的λ次幂(实际上是下一点上信息的增量与“活动空间的信息总量与此刻其所拥有的信息量之差”成正比，但每单位时间每发生一次接触所获得的信息量不变，则实际上是“下一单位时点内信息的增量”就转化为“单位时间内新增加接触次数”).

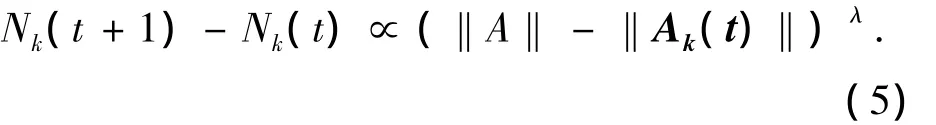
其中:Nk(t)是考察主体k在活动空间上截止到t时刻其所发生的总接触次数，Nk(t+1)是再经过一单位时刻后考察主体所发生的总接触次数，‖A‖是活动空间上的总信息元胞量，‖Ak(t)‖是主体k在t时刻所拥有的信息元胞量.

初始所携带的信息元胞量是个常量，并把每发生一次接触所获得的信息元胞用一个矩阵表示，而此矩阵的测度就是此次接触所获得的绝对信息元胞量.而此刻考察主体所拥有的信息元胞量等于初始所拥有的和后来通过接触所获得信息元胞之和.

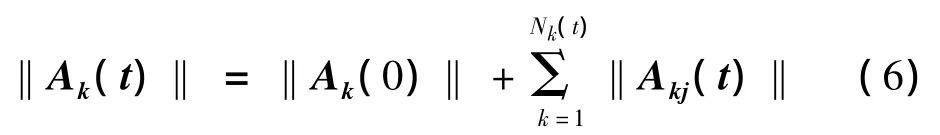
其中:Akj(t)为考察个体k第j次接触所获得的信息元胞矩阵，‖Ak(0)‖是初始携带的信息元胞量，Nk(t)是截止到t时已发生的接触次数，‖Ak(t)‖为截止到t时刻所拥有的信息元胞量，也称信息元胞函数或信息水平.

因不同的考察主体对新信息元胞的敏感好奇程度不同，故其在面对与总信息元胞量同样的差距的情况下，下一单位时间内所发生接触的次数也将不同;即对新信息具有不同的敏感程度的考察个体，将引致其信息元胞总量的增长速度的不同;若较敏感，则其信息元胞数量增长速度较快.选取一个反应不同考察主体表征对信息敏感性的学习品质特征参数σk＞0，则式(6)可整理为

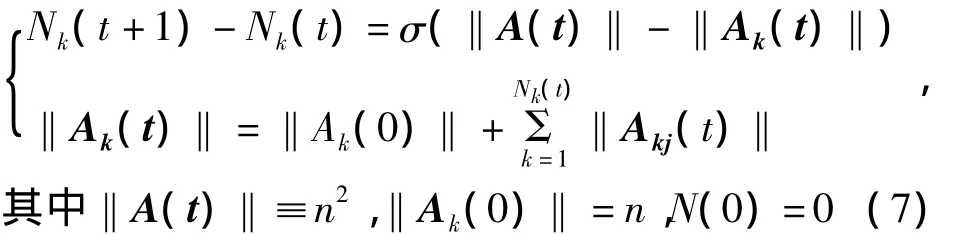
同时为求解方便，不妨令指数λ=1，又因每发生一次接触所获得n/2的信息元胞量相同，即每个信息矩阵的测度都为初始接触所获得单位信息元胞，则上述公式中的第一公式可整理为一个含有参数的且关于“接触次数”的递推公式

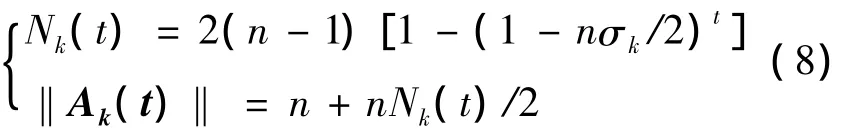
在某个时点上，考察主体总携带的信息元胞量等于初始携带信息元胞量与后来通过接触所获得的信息元胞量之和，而通过接触获得的信息元胞的求解最终归结为对累计发生接触次数的计算，因累计接触次数已知，故信息元胞函数

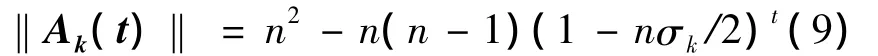
根据上述一系列推理和设定，又由于活动空间内信息元胞量一直大于或者等于考察对象的信息元胞量，故有下述不等式成立

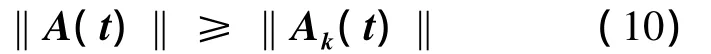
因活动空间上信息元胞总量是个常数，而考察对象任一时点上的信息元胞量已求出，把式(3)和式(9)分别代入式(10)，又因不等式在任一的时刻上恒成立，通过整理，则反映考察主体对新信息灵敏度的参数范围

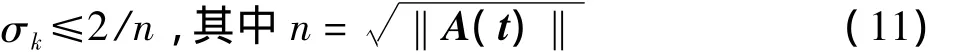
注:如果信息空间的维度和考察主体不一致，则式(11)中2/n的分母应包括信息空间的维度和考察主体的总数两项，而对这些的探讨放在将来的后续工作中.

因设定信息空间的维数与主体数一致，即信息空间的维数越大则主体数也就越多.从式(11)推理可以得出，信息空间的维数越大，则代表某个主体学习品质特征的参数的上限值就越小，这在某种程度上是符合认知法则的.因活动空间上的总信息元胞量不变，并且考察主体在时间的无穷远处才获取活动空间上的所有信息元胞.故“在低维的信息空间中，每单位时间内或者每次接触考察主体获得的信息元胞量与此条件下的总信息元胞量的比值”大于“在信息元胞总量较多的情况下，每单位时间内或者每次接触获得的信息元胞量与此条件下的总信息元胞量的比值”.

根据上述的探究和初始设定，最终把认知法则用一种数学语言表达出来，为直观形象表述这一认知法则(由于客观技术条件的限制，还未能进真人实验模拟，验证上文对认知法则的探究和建立信息元胞方程是否反映真实的认知机制，故行文还仅是一次试探性的先验的理论性探讨)，对方程中的参数进行适当的设定，绘出考察主体信息元胞函数对时间的演化图.看具有不同信息灵敏度的考察主体的信息元胞函数如何改变以及其图形具备什么样的统计特性.

令初始主体数n=100，根据上述分析，故反映考察主体学习品质的参数σk落在0与0.02之间时.在小于0.02的区域内令σk=0.018、0.01、0.002以及0值，则信息元胞函数图依次如图 3所示.

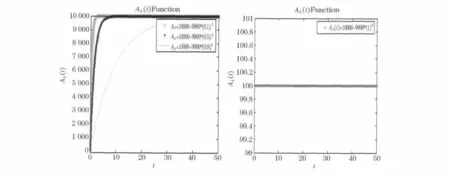
图3 离散的信息元胞函数

从图3中可以看出:1)随时间演化，考察主体所拥有的信息元胞量具有只增不减特性，即曲线单调增加;2)同时认知法则引致的每单位时间内获得的信息元胞量趋于减少也在上图得以反映，即图形上凸;3)不同的学习品质参数σk收敛到活动空间的总信息元胞量，其中σk越大，则收敛的速度越快.并且上述图也说明考察主体具有对已获得的信息元胞不存在遗忘特性.如果考察主体对新获得的信息完全排斥，即反映学习品质的参数值σk=0，则其信息元胞量一直保持在初始水平n上.

3.2 连续型的信息元胞方程

在其他假设条件和分析过程依然保持不变情况下，如果初始的个体足够的多，也就是绝对信息元胞足够的大，上述离散的方程就可改成连续的，故反映信息元胞量的模型为

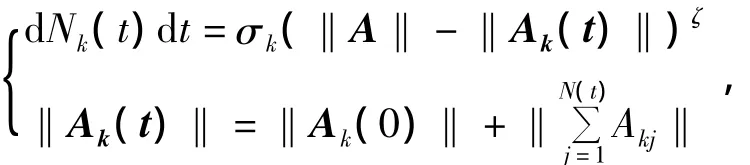
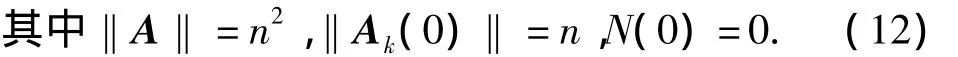
参数σk同样反映考察系统学习品质，同时其依然0在与n/2之间;根据设定，每单位时间接触的人数单调增加;同时接触速度呈现下降趋势，客观的撇开主观上的自满性、存在遗忘以及划分引致信息挖掘的记忆特性.

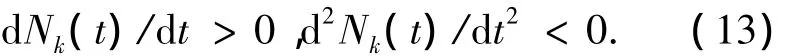
因每接触一个体获得的平均信息元胞量不变，故单位时间内接触的人数逐渐减少，即随着考察个体信息元胞数量的增加，其获得新信息元胞的难度加大.根据这些特性，上述模型又可整理为

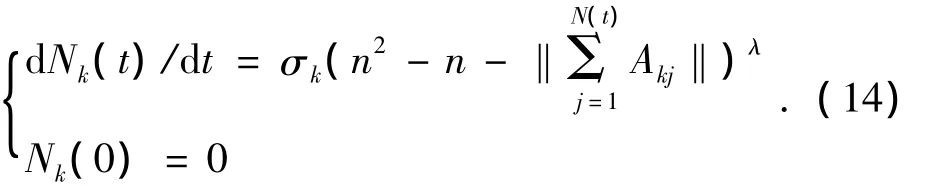
同样令上述指数λ取1，根据上述同样推理:“假定每次获得信息元胞数量相同，即‖Akj‖≡n/ 2”，则在时间(0，t］内考察主体与其他主体发生接触的次数

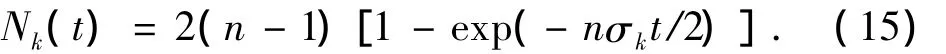
因初始考察主体含有n单位信息元胞，即‖Ak(0)‖，又因任一时点处累计所发生的接触次数由上述公式给出，故考察主体信息元胞函数

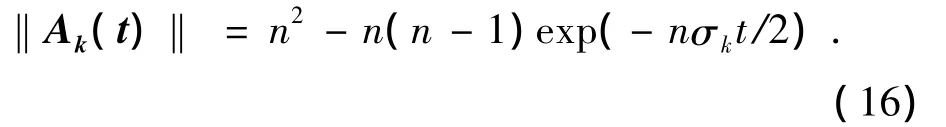
因信息元胞函数是连续的，故在初始的主体数较大情况下才近似成立.在此不妨令n=1 000，反映学习品质的参数σk依次取与上述相同的0.018、0.01、0.002以及0值，则信息元胞函数图如图4.

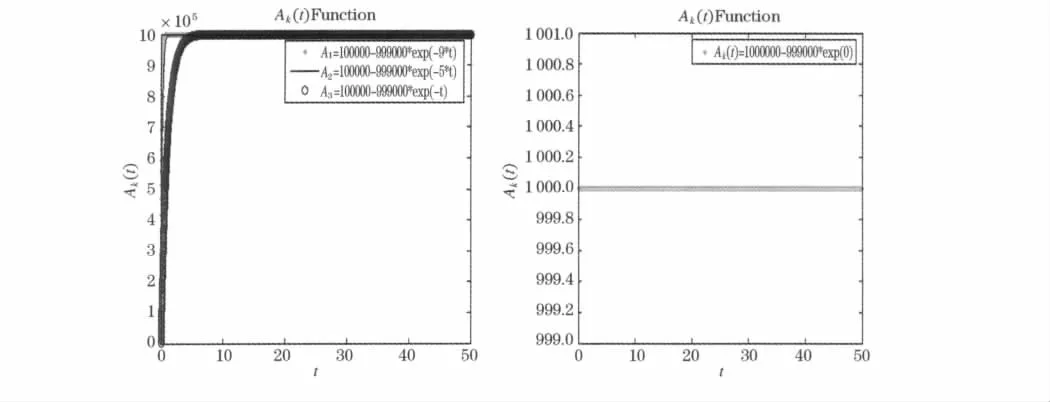
图4 连续的信息元胞函数图

通过图4可看出，图4与离散的信息元胞函数图形颇为相似.因在同样的设定和假设下，信息元胞量具有只增不减特性，上述方程的解就表征为此式.还可以看出在t=0时刻，考察主体有n单位信息量;随着t逐渐变大，考察主体所拥有的信息元胞量将逐渐稳定在特定的单位.若对新获得信息完全排斥，即参数σ=0，则考察主体所拥有的信息元胞量一直保持在初始水平.

3.3 信息元胞方程的延伸

根据初始的分析，随着时间的演化，单位时间内所获得信息元胞量在统计意义上会逐渐下降，下降的方式分为两种.但上述的分析和求解过程主要着眼第一种:每次接触所获得绝对信息元胞量不变，但发生接触的次数逐渐减少;另一种:单位时间内接触的次数不变，但每次接触所获得信息量逐渐递减，正如图1所示，又因两种在结果状态上是等价的，故对上述分析结果只需变形一下，即可生成另一种所需要参量.

如果单位时间内发生接触次数记住正整数，其为一常数;在任一时刻上每接触一次所获得的信息元胞量记为ρk(t)，则信息元胞函数可另写为

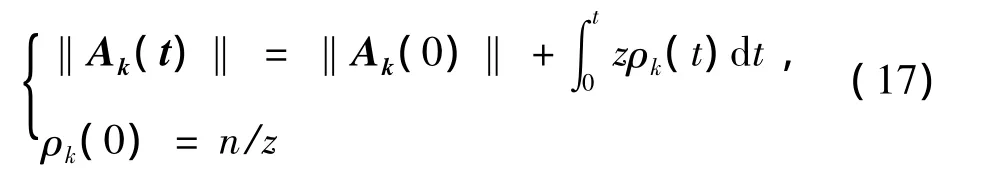
在初始信息量元胞量较大的情况下考虑上述方程，故信息元胞函数可写为上述连续的形式式(16)，把式(16)带入式(17)，并对式(17)的两边求关于时间的一阶导数，则任一时刻t上每接触一次所获得的信息元胞量

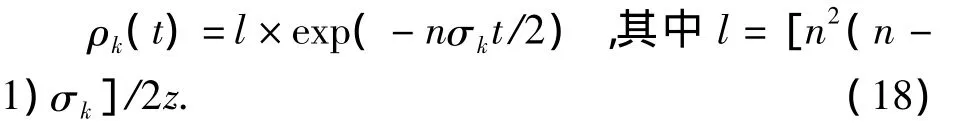
因信息元胞函数是连续，同样令初始主体数n =1 000，每单位时间发生接触次数z=50，反映学习品质的参数σk取与上述相同的0.018、0.01、0.002以及0值，则每接触一次所获信息元胞量ρk(t)图如图5.

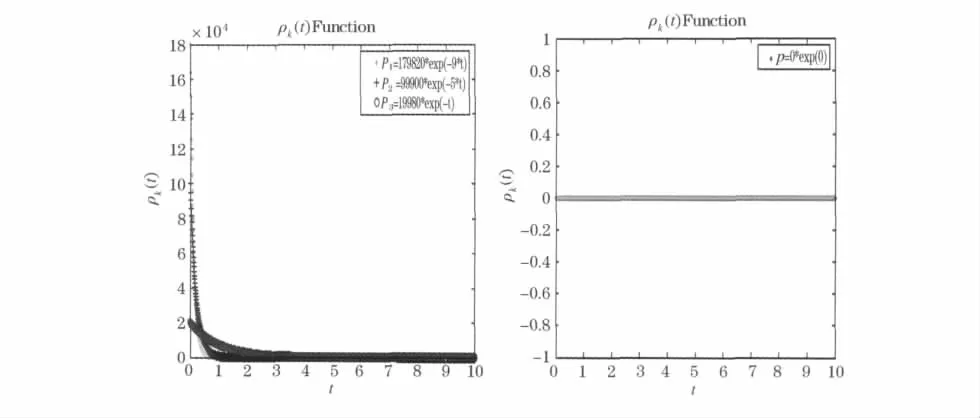
图5 连续的信息元胞密度函数

通过上述可看出:随时间的变化，接触一次所获信息元胞量趋于减少，且收敛于0.反映学习品质的参数σk的参数越大，其起始点越大，且收敛的速度越快，即对信息较敏感的考察个体先接近总信息元胞量，这基本符合设定，即随时间的变化，由于约束每单位时间内所获得的信息元胞量趋于减少;又因考察主体单位时间内发生接触次数一定，故每次接触所获元胞量趋于减少.当参数σk=0，说明虽然发生接触，但考察主体排斥外在信息元胞，故每次接触不会有新的信息元胞被吸纳进考察个体.

4 结语

随着科学的发展，人们越来越发现信息科学中所涌现的现象与行为认知科学有较大的相似.这不是唯象的相似，而有深层次法则上的一致性，即存在一条从信息到认知的数理通路.通过考察个体的信息水平的认知机制，从信息元胞矩阵出发，设定认知假设，采用测度和微分的数学方法，最终给出信息水平的更新方程，而此函数具有“只增不减，但增速放缓”的特性.这为进一步的研究信息和认知科学奠定部分基础，充实了交叉和边缘学科的内容，拉近认知科学和信息科学的距离，进一步丰富了认知中测度的发展，使得信息科学和认知科学在更广义问题上对话.上述工作可归结为应用数学或者系统信息科学范畴，同时也是在严格假设下展开的一次试探性工作，其可以看作进一步研究的参照，但还有诸多不足.

若考虑主观上个体的自满特性，即随着其信息元胞距总信息元胞量越来越近，则自满将引致其信息元胞增加的速度越来越慢，模型就不能仅仅考虑客观上速度放缓的认知法则;若放开对已获得的信息元胞不存在遗忘的限定，则方程中信息元胞量后须加一个随时间变化的遗忘因子;若信息空间的维度与活动空间上的主体数目不同，在接受信息的过程中不符合均匀随机瞬时的认知假定，模型同样得以改进.但上述这些只是对原有模型的添项，如果考虑第三方、划分引致的信息挖掘以及考察内部存在新维度的信息创造源，上述模型须作大的修正，但仅单纯考虑活动空间与考察对象的关系，故无需考虑这些;本文也没有进行真人试验去验证信息元胞方程在模拟个体信息水平上的效力，将进一步研究.

［1］ ZHONG P.A method of image preprocessing based on nonlinear diffusion and information extraction［J］.Computers＆Mathematics with Applications，2011，61(8):2132－2137.

［2］ GUSEO R，GUIDOLIN M.Cellular Automata with network incubation in information technology diffusion［J］.Physica A:Statistical Mechanics and its Applications，2010，389(12):2422－2433.

［3］ DAVIES P B.Formated technology and informated action:The nature of information technology［J］.International Journal of Information Management，2009，29(4):272－282.

［4］ DAVIES P B.Neolithic informatics:The nature of information［J］.International Journal of Information Management，2009，29 (1):3－14.

［5］ ZHANG Q R.Information conservation，entropy increase and statistical irreversibility for an isolated system［J］.Physica A:Statistical Mechanics and its Applications，2009，388(19):4041－4044.

［6］ LAI S C，MAYERKRESS G，SOSNOFF J J，et al.Information entropy analysis of discrete aiming movements［J］.Acta Psychologica，2005，119(3):283－304.

［7］ 邓亿瑞.基于场论的信息扩散研究［J］.情报杂志，2008，27 (8):31－33.

［8］ 程现昆.信息的本质与信息哲学［J］.沈阳工程学院学院学报:社会科学版，2006，2(1):23－25.

［9］ 黄小寒.从不同领域信息学的比较研究再论信息的本质［J］.自然辨证法研究，2005，21(12):87－90.

［10］ 张于心，赵翠霞，马波涛，等.基于信息扩散模型对城际铁路客流分担率的估计［J］.北方交通大学学报，2003，27 (5):52－54.