一种高连通率的传感器网络密钥预分配方法

王 桐，季本洋

(哈尔滨工程大学信息与通信工程学院，哈尔滨150001)

无线传感器网络(WSN)［1］由分布在一个广泛区域内的许多节点组成，传感器节点监测部署区域的信息，实现数据采集和任务监测.当无线传感器网络部署在无人触及甚至敌方控制的环境时，节点将面临各种各样的攻击.因此，如何保证无线传感器网络安全是无线传感器网络研究领域里的重要内容，其中最基本的一项研究内容是密钥管理［2］，主要目的是为传感器节点建立共享密钥，从而为网络提供安全的通信链路.大量研究表明，对称密钥管理方法以其简单高效的特点更加符合未来WSN网络的安全应用.WSN网络对称密钥管理的核心是密钥预分配(key pre-distribution)，其基本实现过程为在网络部署前预先给每一个节点分配一定数量的密钥信息，部署后任何两个需要安全通信的节点使用各自的密钥信息创建出一个共享的成对密钥(pair-wise key)来保护未来产生的通信量. WSN网络密钥预分配方法［3］中密钥的分配在节点部署之前就已完成，解决了无线传感器网络建立后分配密钥所带来的能量消耗问题，成为目前的研究热点.

按密钥的选取方式，目前的无线传感器网络密钥预分配方法可以分成概率性方法和确定性方法两种.概率性方法:Eschenauer和Gligor［4］提出了实际有效的传感器网络概率性密钥预分配方法.该方法为研究传感器网络应用安全保护机制提供了方向性的建议.之后，Haowen等人提出的q-composite［5］方法，使得通信双方能够共有q个密钥，从而增强了网络的健壮性.Liu［6］等人也提出了基于有限域上对称二元多项式的随机密钥预分配方法，通过预分配的对称多项式来计算出共享密钥，但是却带来了较大的计算开销.确定性方法:确定性方法是指在预分配时不是随机选取密钥，而是按照特定模型去构造节点密钥链.第一个确定性密钥预分配模型是由Camtepe［7］等人提出的对称平衡不完全区组设计方法BIBD，为了提高密钥连通概率，该方法利用区组设计和有限影射平面构造密钥预分配模型，可以构造出节点数为n2+n+1，密钥链长度为n+1，每对节点正好共享1个密钥的模型.Lee和Stinson在Camtepe等人的研究基础上提出了TD模型［8］，Du等人提出了基于多密钥空间的增强的Bloom模型［9］等等，但是这些方法存在算法复杂、计算开销大的问题.为了解决上述问题，本文对TD方法进行改进，结合Blom对称多项式算法提出一种无线传感器网络分组密钥预分配方法CCITD (Improved TD scheme based on Crossless Class)，该方法的主要贡献为:1)提高相邻节点之间共享密钥的概率，从而提高了节点之间的连通率;2)可以根据节点存储能力改变节点存储的密钥个数进而使整个网络灵活易变以适应实际需求.

1 相关算法

1.1 Blom矩阵

Blom矩阵［10］利用素域GF(q)上形成的密钥对生成矩阵A×G来定义节点间的密钥对，其中q是能够支持网络节点数的最小的素数，G是一个(λ+1)×N的公共矩阵，N可认为是网络节点数目，λ为网络安全阈值，即只要网络中被俘的节点数不大于λ，就不会对现有节点构成威胁.G通常由范德蒙矩阵生成，因此每个节点只需存储每列的第二个元素就可以衍生出整个列，可以减少节点的存储空间.令A=(D×G)T，D为一个保密的随机对称矩阵，D=(λ+1)(λ+1)，则A×G对应一个N×N的对称矩阵.若记Kmm为A×G中的第m行和第n列的值，则有:Kij=Kji.每个节点根据自己的编号i存储矩阵A的第i行和矩阵G的第i列.当节点i和j要生成共享密钥时，彼此交换自己所存储的的列，然后根据矩阵乘法计算各自的Kij和Kji，由于Kij=Kji，这样节点i和j建立起了对密钥.

1.2 TD方法

Lee和Stinson利用一种特殊的可分组设计(Transversal Design)，构造了一类新的基于组合设计的密钥预分配方法.设(X，B)为一个区组设计，其中:X有v个点，B是X的一个有限子集，称为区组，每个区组都有k个点，且每一个点x都在r个区组中出现，称这样的区组设计是(v，b，r，k)结构，易得bk=vr.如果一个区组设计(X，B)满足对于任意一个元素x∈X，在B的r个区组中出现，且B中任意两个不同的区组Bi，Bj，，至多相交于有一个点，称这样的区组设计(X，B)为一个(v，b，r，k)结构.由这样的(X.B))构造的密钥预分配方法的特点是:对于节点N来说，与其有公共密钥的节点个数达到理论上的最大值.TD(k，n)设计是满足以下条件的三元组(X，B，H):1)X是一个有kn个点的集合，B是集合X的子集构成的集合，其元素Bi(0≤i≤b)称为区组，每个区组Bi都含有k个元素，2)H是X的一个划分，分成k组，每组n个点，3)每一个组H和每一个区组Bi(0≤i≤b)只有一个点相同;4)从不同组任意选出两个点x，y，恰好只在一个区组中同时出现.

2 基于不相交类的密钥预分配方法

对TD方法进行改进，提出基于不相交类的密钥预分配方法CCITD(Improved TD Scheme based on Crossless Class).

首先，根据TD方法，提出一个基于不相交类的TD(k，n)模型.模型包含个点，把kn个点分成个集合，每个集合包含n个点，集合被称为组(这里的组指的是模型中的组，而不是传感器节点组)，取kn点中的k个点组成区组，区组的集合设为B区组可以被分成B1，B2，…，Bn个集合.

定义1 不相交类:对于每一个集合B，每一个点只在其中的一个区组出现一次.这些区组的集合B被称为不相交类.

从以上的定义可知，有n2个区组，每个区组包含k个点，每个区组只和每个组的一个点相交.有n个不相交类，每个不相交类包含n个区组，在同一个不相交类中的两个区组不包含相同的点.

举例说明，以下是一个基于不相交类的TD(3，5)模型，这个设计包含15个点，将点分成3个组G，每个组包含5个点.共有5个不相交类，每个不相交类包含5个区组，每个区组包含3个不同的点，设点的集合为{00，01，02，03，04，10，11，12，13，14，20，21，22，23，24)}.

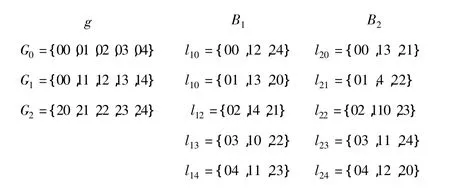
可以发现，每个点只在一个组Gi中出现，每个区组Li从每个组G中取一个点组合而成，每个点只在一个不相交类Bi中出现一次.在CCITD方法中，把点和密钥相对应，区组和节点相对应，要利用设计的不相交类分配组内的节点.在阐述CCITD方法之前，先来考虑组内和组间密钥的分配过程.

考虑一个n组节点的传感器网络，每组中有n个传感器节点，对于初始值n，可以把设计出来的区组和传感器节点相关联，包含区组的不相交类和传感器节点组相关联.

对于CCITD(k，n)(1＜k＜n)，以增加存储量为代价，增加一个变量k以提高不同传感器节点组之间的连通率.考虑传感器节点数量为n2的情况.当λ是的n的除数的时候，通过把TD(k，n)的n个不相交类分成λ个不相交的集S1，S2，…Sλ，每个集合包n/λ含个不相交类，并且让不相交类中的区组和节点组中的传感器节点相对应，当传感器节点组群数量比较小的时候，这种方法可以保持高连通率.

CCITD方法中的点和Blom矩阵的t次对称多项式相关联.因此，不同节点组间节点对能够建立密钥连接，每个节点需要存储k(t+1)个密钥.在CCITD方法中，通过在每个不相交类中引入独立的基于多项式方法来减少节点间密钥计算的难度，提高节点连通率，对于不同节点组的节点，也会通过不相交类来实现连接.

定义2 CCITD方法:给出一个初始变量n，一个非负整数k(1≤k≤n)，一个组数λ和一个t，0≤n2/λ-1-1，使用TD(k，n)来建立一个密钥预分配方法，n2个节点分布在λ个组中(G1，G2，…，Gλ)，每个组中含有n2/λ个节点.

1)CCITD(k，n)将n个P1，P2，…，Pn不相交类分成λ个集合，每个集合含有n/λ个不相交类，用S1，S2，…，Sλ来表示每个集合.每个集合含有n2/λ个区组.

2)传感器节点对应CCITD方法中的区组，传感器节点对应组Si.

3)一个Blom矩阵的t次对称多项式对应于CCITD方法中的点，将点分配给相应的区组.

4)一个Blom矩阵的t次对称多项式被分配给每一个不相交类Pi，1≤i≤n，之后通过把这个多项式分配给相应节点(这些节点所对应的区组被包含在不相交类Pi中).表1总结了密钥预分配方法和CCITD方法的对应关系.

表1 无线传感器网络和CCITD方法的对应关系

下面对 CCITD方法进行举例说明，假设CCITD(3，5)，t=1，构建25个节点，分布于5个部署组中，每个部署组中5个节点，每个节点存储对应的8个密钥.n/λ=1，所以每个集合Si只包含一个不相交类.假设第1组节点含有IDs l，m，r，s，t.第2组节点含有IDs u，v，w，xy把和点(point)相对应的Blom多项式表示为，把和每个不相交Bi类对应的Blom多项式表示为，则前两个节点组如下所示

应用CCITD方法建立的密钥预分配方法具有如下性质:

1)每个节点相当于存储(k+1)(t+1)个密钥.

2)对于每个Blom矩阵的多项式，有n个节点应用到那个Blom多项式.

3)q=k/n.

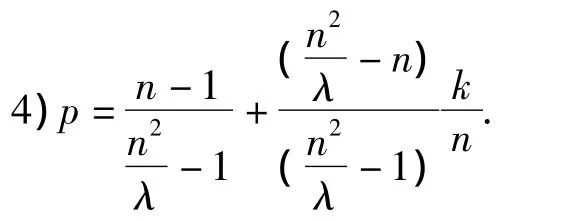
证明:

1)每个CCITD(k，n)中的区组都包含k个点，且都被包含在一个不相交类中.每个节点存储k+ 1个Blom多项式，所以每个节点要求存储(k+1) (t+1)个密钥.

2)每个CCITD(k，n)的点被包含在n个区组中，每个不相交类正好含有n个区组，因此每个Blom多项式分配给n个节点.

3)如果不同组的两个节点对应的区组相交，那么他们拥有一个共同的Blom多项式，因为设计的区组中每个含有k个点，每个点还位于n-1个其他的区组中，所以不同组间节点共享密钥的概率为k(n-1)/(n2-n)=k/n=q.

4)对应于同一个不相交类中的区组，两个节点来自同一个组的概率为(n-1)/(n2/λ-1)，在这种情况下，他们拥有共同的Blom多项式.相反的，节点对应的区组分布在不同不相交类中的概率为(n2/λ-n)/(n2/λ-1)，在这种情况下，他们拥有相同Blom多项式的概率为k/n.因此同一组中随机抽取两个节点，他们拥有相同密钥的概率为.

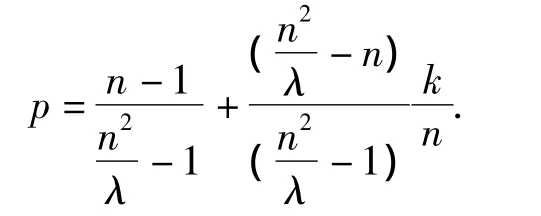
可以发现，对于λ＞1，q＜p.

3 分析与评价

3.1 节点连通度

如果一组中的2个节点是相邻节点，那么通过一跳或者二跳建立连接的概率是

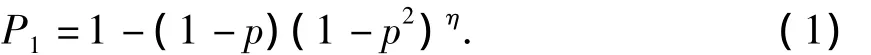
其中:η是组内相邻节点数，p是组内节点建立直接密钥的概率.

考虑同组内的一对相邻传感器节点不能共享一对密钥的概率为1-p.对于每一个普通的相邻节点，通过2跳路径无法建立连接的概率为1-p2.因此，节点间无法通过两跳来建立共享密钥的概率为(1-p)(1-p2)η.

如果两个相邻节点分别属于不同的部署组，那么它们通过1跳或者2跳建立连接的概率为

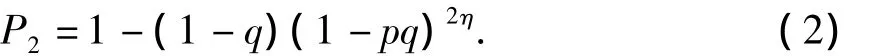
其中:η为相邻节点数，p为组内节点共享密钥的概率，q为组间节点共享密钥的概率.

两个来自不同组的相邻节点不能共享密钥的概率为(1-q).在它们的组内这些节点有η个普通相邻节点.对于每一个这样的相邻节点，节点不能通过这个相邻节点建立两跳连接的概率为(1-pq).因此，在它不能通过一跳或者两跳建立连接的概率为(1-q)(1-pq)2n.所以，他们能通过1跳或者2跳建立连接的概率为1-(1-q)(1-pq)2η.

3.2 仿真结果和性能对比

仿真过程如下，设计一个10 000个节点的传感器网络，给出CCITD(25，100)，假设η=7，结合CCITD方法中的p、q以及公式(1)，(2)得到如图1的仿真结果，横坐标表示传感器节点分组的数目，纵坐标表示CCITD方法相邻节点间的连通率.

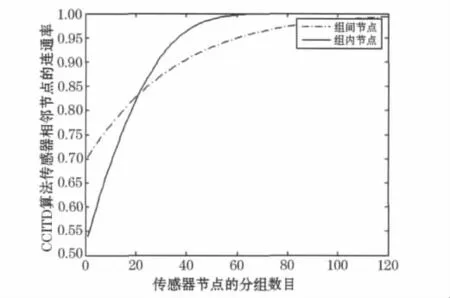
图1 CCITD密钥预分配方法中相邻节点之间共享密钥概率

由图1可知，本地连接概率随着节点组组数的增加而提高，并且组内和组内节点连通率都保持在一个较高的水准.

为了与 CCITD方法进行对比，部分实现了Liu［10］的方法，将10 000个节点分布在λ个组中，参数η=7，结合公式1，2，得到如图2的仿真结果.图2的横坐标表示传感器节点分组的数目，纵坐标表示不同组间传感器相邻节点的连通率.可以发现对于不同组的传感器节点，CCITD方法的不同组间节点连通率远高于Liu的方法.这是因为传统分组密钥预分配方法组间密钥共享概率很低，严重影响整体连接，整个组群可能与网络断开连接，此外，即使组群正在连接之中，少数节点必须承担组群中的通信负担，很可能使组群的通信出现瓶颈.

Liu的方法要求组内节点的连通率为100%，当每个节点组很大时，独立的成对密钥对存储的需求变的非常高.另一方面，当组群数量变小时，基于多项式算法的抗捕获性也会变弱.无法调整的连接意味着对于节点数量比较大的组群，Liu的方法是不合适的.而CCITD方法比较好的解决了这个问题［11-12］.

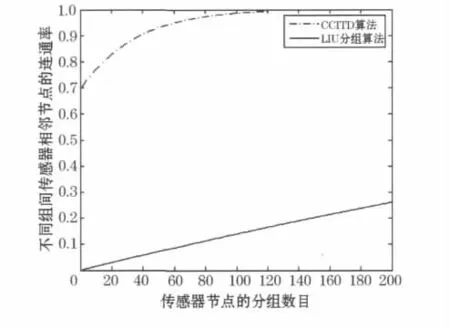
图2 CCITD方法和Liu的方法中不同组间相邻节点间共享密钥概率对比

另外CCITD(k，n)方法中每个节点存储个密钥，增大则节点存储的密钥数量增加，节点间的连通率提高，但是这样传感器节点的存储量就会变大，能量消耗也会变大，因此，可以根据实际需要来规定的值，以达到连通率和节点存储量的平衡.

4 结语

本文提出一种改进的无线传感器密钥预分配方法CCITD，该方法的优势在于:可获得较好的相邻传感器节点间连通率;可动态的、根据实际需要去改变节点数量，节点组数量以及节点中所存储的密钥数目，从而适应不同应用环境对传感器网络的需求.

［1］ 孙利民，李建中.无线传感器网络［M］.北京:清华大学出版社，2005.

［2］ 苏 忠，林 闯，封富君，等.无线传感器网络密钥管理的方法和协议［J］.软件学报.2007，18(5):1218-1231.

［3］ 夏戈明，黄遵国，王志英.基于对称平衡不完全区组设计的无线传感器网络密钥预分配方法闭［J］.计算机研究与发展，2008，45(l):154-164.

［4］ ESCHENAUER L，AND GLIGOR V D.A key-management scheme for distributed sensor networks［C］//Proceedings of the ACM Conference on Computer and Communications Security (CCS’02)，ACM，New York，2002，41-47.

［5］ CHAN H，PERRIG A，SONG D.Random key pre-distribution schemes for sensor networks［C］//Process of IEEE Symposium on Research in Security and Privacy，Berkeley:IEEE Computer Society，2003:197-213.

［6］ LIU D，NING P.Establishing pairwise keys in distributed sensor networks［C］//Process of the 10th ACM Conference on Computer and Communications Security，New York:ACM Press，2003: 52-61.

［7］ CAMTEPE S A，YENER B.Key distribution mechanisms for wireless sensor networks:a survey［R］.Tech.rep.TR-05-07，Rensselaer Polytechnic Institute，2005.

［8］ LEE J，STINSON D R.On the construction of practical key predistribution schemes for distributed sensor networks using combinatorial designs［J］.ACM Trans.Inform.Syst.Secur.，2008，11(2):1-35.

［9］ WEN L D，JING D.A pairwise key predistribution scheme for wireless sensor networks［C］ //Proceedings of the 10th ACM conference and communications Security，New York:ACM Press，2003:42-51.

［10］ BLOM R.An optimal class of symmetric key generation systems［C］//Proceedings of EUROCRYPT’84.Lecture Notes in Computer Science，Berlin:Springer-Verlag，1985(209):335 -338.

［11］ LIU D，NING P，DU W.Group-based key pre-distribution in wireless sensor networks［J］.ACM Trans.Sen.Netw.，2005，4(2):1-30.

［12］ 黄 玲，陈东彦，王攀宇.数据包错序的多包传输网络控制系统研究［J］.哈尔滨商业大学学报:自然科学版，2011，27 (6):857-861.