基于岭估计的概率积分法预计参数的求取

王明柱，郭广礼，王 磊，王 彬

（1.中国矿业大学江苏省资源环境信息工程重点实验室，江苏徐州221116;

2.中国矿业大学国土环境与灾害监测国家测绘局重点实验室，江苏徐州 221116）

基于岭估计的概率积分法预计参数的求取

王明柱1，2，郭广礼1，2，王 磊1，2，王 彬1，2

（1.中国矿业大学江苏省资源环境信息工程重点实验室，江苏徐州221116;

2.中国矿业大学国土环境与灾害监测国家测绘局重点实验室，江苏徐州 221116）

采用最小二乘拟合求取概率积分法预计参数时，经常遇到发散问题，致使求参结果失真。而求参过程中法矩阵的病态是造成结果发散的主要原因之一。将岭估计应用于预计参数的求取中，能够有效地克服传统最小二乘拟合求参时法矩阵的病态。在给出基于岭估计求参模型的同时，使用Matlab实现了参数的自动求取。最后通过模拟算例验证了该求参模型克服法矩阵病态的有效性及求参结果的可靠性。

岭估计;概率积分法;求参;开采沉陷;L曲线法

概率积分法是进行开采沉陷预计的主要方法，预计过程中预计参数的准确性决定了地表移动变形预计的精度。参数的影响因素主要有:覆岩的岩性和地层结构、采深、采厚等［1］。我国大部分矿区都根据所设的地表移动观测站反演出了适合自己矿区的概率积分预计参数。

预计参数的求取通常采用最小二乘拟合的方法，该方法计算简单，且求参精度能满足工程需求。而最小二乘拟合求参过程中法矩阵一旦病态，就致使迭代结果发散、失真，造成求参困难。为解决由于法方程系数阵病态而导致最小二乘估计不稳定问题，统计学家们提出了岭估计、广义岭估计、主成分估计等有偏估计来改善这种情况下的最小二乘估计。岭估计法从减小均方误差的角度出发，最初由A.E.Hoerl于1962年提出，并于1970年由他和R.W.Kennard对该方法做了系统的发展。该方法成为目前使用最多的一种有偏估计［2］。

采用岭估计可有效克服病态矩阵干扰，使求参结果更可靠，确保概率积分法开采沉陷预计精度。

1 岭估计

1.1 岭估计基本原理

设有观测方程:

式中，L是观测值;A是系数阵;X是待估计参数的真值;Δ是噪声，Δ～N（0，δ20I）。则上式常规的最小二乘解为

若法矩阵N=ATPA条件数很大，即为病态矩阵时，求逆就会出现不稳定，致使最小二乘估计的方法不可能得到未知参数的精确估值［3］。岭估计法可解决这类问题［4］。其基本思想是利用原最小二乘估计的数学模型，在其法方程系数矩阵N的对角线上加上一个很小的正数来抑制法方程的病态，是一种在均方误差意义下优于最小二乘估计的有偏估计方法，是最小二乘估计的线性组合。的岭估计解为［2］

式中，k为岭参数。可见，岭估计结果与岭参数k有关，选择不同的岭参数，估计结果可能差异很大，所以岭估计的关键是选择合适的岭参数。

1.2 岭参数的确定

关于岭参数的确定，目前已经有不少的方法，如岭迹法、L曲线法、两步解法及GCV法等，但是到目前为止还没有一种公认的好方法。相比较而言，L曲线法易于确定岭参数，是一种确定岭参数的良好方法［5］。本文使用L曲线法来确定岭参数，在此进行简述，其他方法可参见文献 ［5－7］。

根据正则化原理，（1）式的岭估计准则为

求上式最大值就可得到最大曲率KLmax，其对应点即为所求点。然后求出该点所对应的岭参数k，即为 （1）式所需要的k。具体求解过程可参见文献 ［8］。

2 概率积分法预计参数的岭估计模型

2.1 求参的岭估计模型

概率积分法预计参数可由地表点实测移动变形资料求出。当布置的测点为正规观测站时，可采用最小二乘曲线拟合法;当测点为非正规观测站即一系列散点时，可采用最小二乘曲面拟合法。若最小二乘的法矩阵病态，则易造成求参结果失真、不可靠。基于岭估计的曲面拟合法不仅可以有效地抵御法矩阵病态的干扰，还可适用于非正规观测站和残缺观测站资料的求参。

概率积分法的预计参数有下沉系数q、主要影响角正切tanβ、主要影响传播角θ、拐点偏移距S1，S2，S3，S4及水平移动系数b。其任一点移动变形预计具体计算公式可参见文献 ［1］。进行基于岭估计的曲面拟合法求参时，首先利用实测地表下沉值来求取q，tanβ，θ，S1，S2，S3，S4这7 个参数。然后，认为这些参数已知，再利用地表点的水平移动观测值进行迭代拟合求取b。

根据任一点移动变形预计公式，任一点下沉Wi可表示为任一点坐标 （xi，yi）和参数q，tanβ，S1，S2，S3，S4和 cotθ的函数，即

由（4），（5）式确定岭参数k，则7个参数改正数的岭估计解为

接下来基于岭估计的迭代求参过程同上述由实测地表下沉值求参，在此不赘述。

2.2 求参结果的精度评定

所求取参数的效果如何，可通各参数的均方误差和各点拟合中误差来考查。

2.2.1 计算各参数的均方误差

2.2.2 计算各点拟合中误差

根据上述的求参岭估计模型，使用Matlab程序实现了各参数的自动求取及参数的精度评定。

3 算例分析

通过模拟算例来检验该模型抵御法矩阵病态的效果及求参的可靠性。

模拟开采一个近水平煤层，采厚为3m，平均采深为300m，工作面详情见表1。工作面上方布设2条地表移动观测线 （图1）:一条走向观测线，一条与走向成45°夹角的观测线。共设有观测点94个，点间距约20m。确定 7个参数 q，tanβ，θ，S1，S2，S3，S4（表2），用概率积分任一点下沉预计公式计算出各测点下沉值，然后在各下沉值中加入标准差为10mm的随机误差，以此作为下沉观测值进行参数反演。

表1 工作面信息

表2 预计参数真值

图1 观测线布设

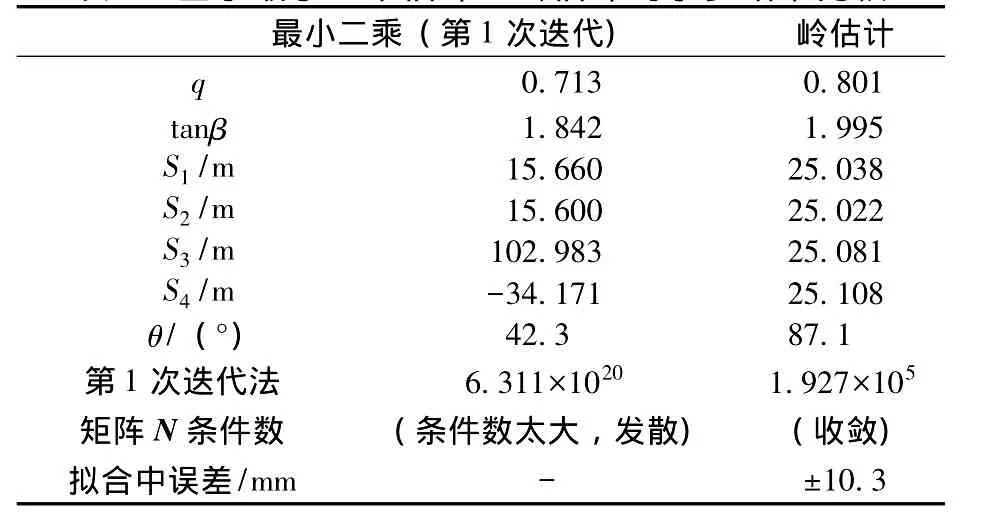
表3 基于最小二乘估计、岭估计的求参结果比较

最小二乘估计法第1次迭代计算时法矩阵N极度病态，其条件数数量级达1020，经第1次计算后部分参数已很大程度上偏离真值。继续迭代计算后，各参数仍不收敛，最终计算结果发散。而岭估计法大大改善了法矩阵的病态，第1次迭代计算时，其条件数数量级降为105。且迭代计算过程中，随着各参数收敛于其真值，法矩阵条件数也愈小。

将基于岭估计求得的各预计参数与表2中的真值相比，其精度足够满足预计工作的需要。最终各点下沉值的拟合中误差为±10.3mm，接近于在原真值基础上所加入的标准差为10mm的高斯白噪声。验证了该模型求参的可靠性。

4 结论

（1）在使用最小二乘估计求取概率积分法预计参数时，存在由于法矩阵的极度病态，致使求参结果发散的问题。

（2）岭估计法能够很好地改善法矩阵的病态性，较最小二乘估计其难点仅在于岭参数的确定。所采用的L曲线法能够方便准确地求出岭参数，使岭估计模型抗病态效果显著。

（3）基于岭估计的概率积分法求参模型，具有较好地抵御矩阵的病态性能，使求参结果更可靠。所建立的模型适用于全盆地的拟合求参，能够处理不规则以及不完整的观测站资料。

［1］何国清，杨 伦，凌赓娣，等.矿山开采沉陷学 ［M］.徐州:中国矿业大学，1991.

［2］崔希璋，於宗俦，陶本藻，等.广义测量平差 （第二版）［M］.武汉:武汉大学出版社，2009.

［3］黄幼才.岭估计及其应用［J］.武汉大学学报 （信息科学版），1987，12（4）:64－73.

［4］Hoerl A E，Kennard R W.Ridge Regression:Biased Estimation for Non－orthogonal Problems［J］ .Technometrics，1970，12（1）.

［5］汪明瑾，王静龙.岭回归中确定K值的一种方法［J］.应用概率统计，2001，17（1）:7－13.

［6］黄海兰，牛 犇.岭参数确定的研究［J］.测绘科学，2011，36（4）:31－32.

［7］王振杰，欧吉坤.用L－曲线法确定岭估计中的岭参数 ［J］.武汉大学学报 （信息科学版），2004，29（3）:235－238.

［8］ Hansen P C，O＇Leary D P.The Use of The L－curve in The Regularization of Discrete Ill－posed Problems［J］ .SIAMJ.Sci.Com put，1993，14（6）:1487－1503.

［9］中华人民共和国煤炭工业部.建筑物、水体、铁路及要井巷煤柱留设与压煤开采规程 ［M］.北京:煤炭工业出版社，1986.

［10］张翠英.基于MapX的煤矿开采沉陷预计及地表移动观测站数据处理系统的研发［D］.淮南:安徽理工大学，2009.

Prediction Parameters Calculation of Probability Integration Method Based on Ridge Estimate

WANG Ming-zhu1，2，GUO Guang-li1，2，WANG Lei1，2，WANG Bin1，2
（1.Key Laboratory of Resources Environment Information Engineering of Jiangsu Province，China University of Mining ＆ Technology，Xuzhou 221116，China;2.Key Laboratory of Land Environment and Disaster Monitoring of State Bureau of Surveying and Mapping，China University of Mining＆Technology，Xuzhou 221116，China）

Divergence problem will often result in parameters distortion in solve prediction parameters of probability integration method with least square method.Morbidity of normal matrix is one of main divergence reasons.Ridge estimate was applied in solving prediction parameters，which could effectively overcome distortion of normal matrix.At the same time，Matlab was used to realize parameters＇automatic solving.A simulation example was present to verify the model.

ridge estimate;probability integration method;parameter solve;mining subsidence;Lcurve method

TD325.2

A

1006-6225（2012）02-0017-03

2011－11－05

国家自然科学基金重点项目 （50834004）;国家公益性行业基金资助项目 （200811050）;中国矿业大学青年科研基金资助项目（09091252）

王明柱 （1986－），男，江苏丰县人，硕士研究生，主要研究方向为开采沉陷与“三下”采煤。

［责任编辑:王兴库］

基础研究