不同边界下的坚硬顶板极限承载分析及破断距确定

黄耀光，浦 海

（1.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州221008;2.中国矿业大学力学与建筑工程学院，江苏徐州 221116）

不同边界下的坚硬顶板极限承载分析及破断距确定

黄耀光1，2，浦 海1，2

（1.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州221008;2.中国矿业大学力学与建筑工程学院，江苏徐州 221116）

煤矿开采地质条件复杂以及不同煤层采煤方法的差异，导致采场顶板会有多种边界条件。在不同边界下，坚硬顶板的极限载荷和破断距必不相同。因此，建立5种不同边界 （四边固支、三固一简、邻固邻简、对固对简及三简一固）下顶板的力学模型，利用塑性极限法求得各种边界下顶板极限载荷，分析得出极限载荷随k（推进距离与工作面长度比）的变化规律。顶板极限载荷在对边固支和对边简支边界下最大，四边固支边界次之，而在其他3种边界下接近相等。此外，以所求顶板极限载荷为基础，得到了各种边界条件下顶板的最小破断距，并采用数值试验方法进行了验证。

不同边界条件;坚硬顶板;极限载荷;破断距

在煤矿开采过程中，随着原煤不断采出，煤上方的覆岩层将会悬露出来而形成悬空的顶板。由于顶板对上覆岩层起支承作用，随着工作面推进，顶板宽度将增大，从而使顶板承载能力发生变化。如果顶板上覆载荷超过了顶板的极限承载力，则有可能引起采场巷道顶板断裂、垮落等严重的顶板事故［1－2］。所以需要对顶板进行控制，以预防顶板事故的发生。

而在顶板的控制中，顶板的极限承载能力和破断距是2个重要的参数，决定着顶板支护方案等地选择。由于采矿工程中，地质条件极其复杂，而且对不同的煤层所选用的采煤方法也不相同，这就造成了顶板边界条件的复杂性［3］。显然，不同边界下顶板的极限承载力和破断距是不同的，因此，为了给顶板控制提供更准确的依据，就需要确定不同边界条件下顶板的极限承载能力及破断距。

在研究顶板的极限承载力和破断距时，最先采用的是梁理论［4－6］。但是梁理论分析方法只适用于应力和应变等效的情况［6－7］。而采矿中所形成的顶板大多不满足这一条件，特别是具有一定厚度的坚硬顶板，这就使得用梁模型所得结果较大偏离实际。因而在对顶板进行分析时，建立顶板的板结构模型更符合采矿实际情况。

1 不同边界下顶板力学模型

采矿过程中所形成的坚硬顶板，因其厚度与工作面推进距离的比值较小，符合薄板的假设［4］，故可将采场顶板视为矩形薄板。在建立顶板的力学模型时，一般将采场的窄煤柱视为简支边界，而将实体煤视为固支边界［8］;若有断层存在时，则将顶板的断层边界视为简支边界［9］。由于不同的地质条件 （如断层等）和采煤方法的差异，顶板将会出现不同的边界条件，所以需要建立相应的顶板力学模型。其主要有以下几种边界条件:若顶板四周均为实体煤或初始工作面，则可将顶板边界简化为四边固支边界，其力学模型如图1（a）所示;若顶板有一工作面为留有小煤柱的采空区或与断层边界相连，而其余三边为实体煤，则可将顶板边界简化为三边固支一边简支边界，其力学模型如图1（b）所示;若顶板的一个工作面方向和相邻的工作面推进方向为实体煤，而其余两边是留有小煤柱的采空区或断层边界，则可将顶板边界简化为两邻边固支和两邻边简支边界，其力学模型如图1（c）所示;若顶板的相对工作面方向为实体煤，而相对工作面推进方向为断层边界或留有小煤柱的采空区，则可将顶板边界简化为对边固支和对边简支边界，其力学模型如图1（d）所示;顶板的一个工作面为实体煤，而另外三边为留有小煤柱的采空区或与断层边界相连，则可将顶板简化为三边简支和一边固支边界，其力学模型如图1（e）所示。

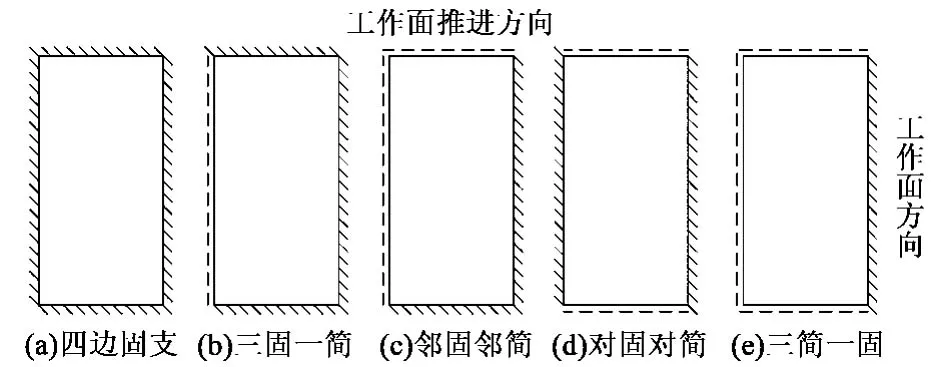
图1 不同边界下顶板力学模型

2 坚硬顶板极限承载分析

2.1 顶板极限分析方法

顶板岩体为脆性材料，其弹性变形相对较小。但顶板岩体并不会因某一点达到屈服就完全破坏，而是随着载荷不断增大，顶板屈服会不断扩展下去，并形成一条条塑性铰线。在这些塑性铰线上，顶板仍旧可以承受极限弯矩，并且塑性铰线可以转动［7，9］。只要顶板保持几何不变性，塑性铰线将会一直发展下去，直至顶板成为几何可变机构而最终破坏。当顶板破坏时，顶板内的塑性铰线将顶板分割成若干块体区域。

顶板岩体由于塑性铰线发展而达到破坏的临界点时，顶板所受内力和外力仍处于平衡状态。假设给该平衡状态一个微小扰动，则外力在虚位移w（x，y）上所作的功为

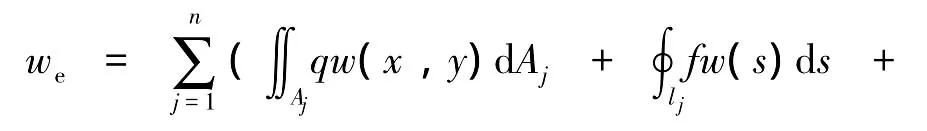
式中，θj为板块j的法向转角;Msj为极限弯矩在塑性旋转轴上的投影，Lj为总的投影长度。

则由虚功原理知，顶板外力在扰动下所做的功（we）和内力所作的功 （wi）应相等，即有:

从上式中可以解得载荷q的表达式。再通过对其求极值，便可得顶板的极限载荷qs，此即为分析顶板极限载荷的屈服线分析法［10－11］。

2.2 坚硬顶板极限承载分析

对于采矿中的各种边界条件下的矩形顶板，已经由相似模拟实验和理论分析得到了其断裂形态［4，10，12－13］。由此，可以得到不同边界条件下顶板可能的塑性破坏结构模型，如图2。在所有可能的破坏结构中，载荷最小的一个称为顶板的极限载荷，与其相对应的破坏结构即为顶板的最佳破坏机构。

式中，n为塑性铰线所分割的顶板块体数，m为所分割顶板块体数目中受集中载荷的块体数，m≤n;第1，2，3项分别为均布载荷、线载荷和集中载荷所作的功。

而在微小扰动下，顶板内力所作虚功为极限弯矩在塑性旋转轴上的投影与板的相应转角θ以及投影长度的乘积，即为

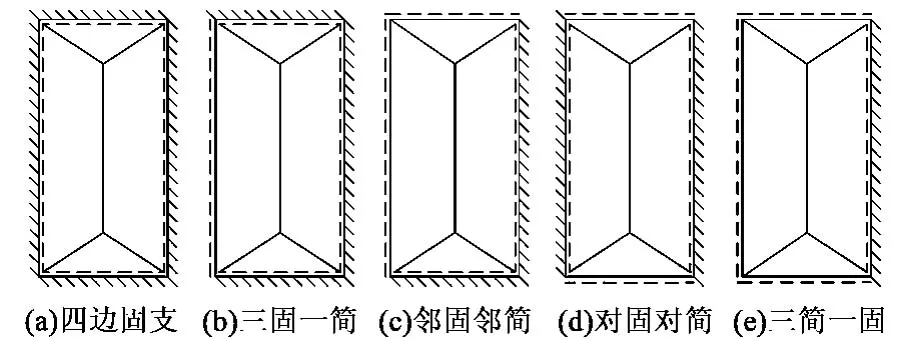
图2 不同边界下顶板破坏结构

顶板在破坏过程中，将在固支边界处形成与其边界重合的塑性铰线，而在简支边界处不形成塑性铰线。因此，对于三边固支一边简支矩形顶板而言，由于顶板受均布载荷，且两工作面推进方向均为固支边界，因此，顶板形成的塑性铰线关于工作面方向的中心线对称。故可设顶板内部塑性铰线的交点距X=±a/2边界的距离相等，设为x。而将沿X轴方向的塑性铰线距Y=b/2边界的距离设为y。由此，得该顶板的极限载荷求解模型如图3。

假设顶板的最大虚位移为δ，且其极限弯矩为Ms。则由于顶板仅受均布载荷，按公式 （1）积分可将顶板外力所做功表示为

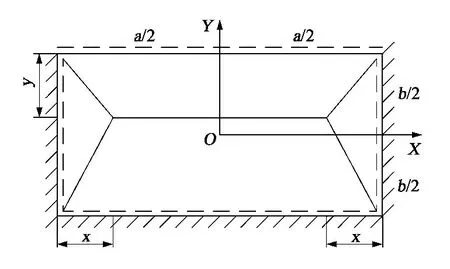
图3 三固一简顶板极限载荷求解模型

则由虚功原理we=wi可求得顶板的载荷表达式为

在求解其他4种边界下顶板的极限载荷时，可以按相同的方法进行计算。但需注意，只有固支边界才形成塑性铰线，而简支边界不形成塑性铰线。并且根据不同边界条件下顶板的对称性，可以相应减少计算量。表1为所求的各种边界条件下，顶板的载荷表达式、最佳破坏机构以及顶板的极限载荷qs。为了能够更清楚地看出不同边界条件下顶板的极限载荷qs的变化规律，将其随k的变化规律用图4表示。

表1 各种边界下的顶板极限载荷

从图4可以看出，在5种不同边界条件下，顶板的极限载荷的变化趋势相一致，即都随着k值不断增大而减小，且在k＜0.25之前，顶板的极限载荷减小很快;之后变得相当缓慢。顶板的极限载荷都在k=1.0附近趋于零，接近失去承载力。但在相同的k值下，不同边界条件下顶板的极限承载能力是不相同的。其中，当顶板为对边固支和对边简支边界时，顶板的极限载荷最大。因而，在采矿工程中，应尽量使顶板处于此种边界条件下，以充分发挥顶板的自身承载能力。而当顶板为三边固支和一边简支或邻边固支和邻边简支或三边简支和一边固支边界时，顶板的极限承载能力接近相等。

3 坚硬顶板破断距分析

3.1 顶板破断距的确定

图4 顶板极限载荷qs随k变化规律

在采矿工程中，采场工作面的长度在确定之后，往往保持不变，而工作面的推进距离却会不断变大。随着工作面推进距离增大，采场顶板结构将发生变化，这使得顶板的承载能力将会发生变化。如果任由工作面推进距离增大而不加控制，则采场坚硬顶板可能由于顶板结构的过分变化从而导致其发生垮落等破坏。因此，为了采矿的安全生产，需要确定采场顶板的破断距。

上一部分中，在假定工作面长度a和工作面推进距离b不变的情况下，得到了顶板的极限载荷qs。为了求得顶板的最小破断距bmin，可以假定顶板所受均布载荷q及工作面长度a不变，并令顶板的极限载荷qs=q。从而依据表1所得的顶板的极限载荷公式，反解求得顶板的最小破断距bmin。在此，仍以三边固支和一边简支顶板为例，即有

采用相同的方法，对其他4种边界条件下的顶板进行求解，可以求得各种边界条件下顶板的最小破断距，其结果用表2列出。

表2 各种边界条件下顶板的最小破断距

3.2 数值验证

某矿的顶板岩体为中砂岩层，其力学性质［3］如下:弹性模量为25GPa，抗拉强度极限 σs为7MPa，泊松比为 0.28。采场工作面长度是150.0m，顶板岩层厚为4.0m，上覆岩层均布载荷q为174.7kN/m。

依据弹性薄板问题中应力与弯矩的关系

则将已知的坚硬顶板的极限应力代入公式（11），可得顶板的极限弯矩为

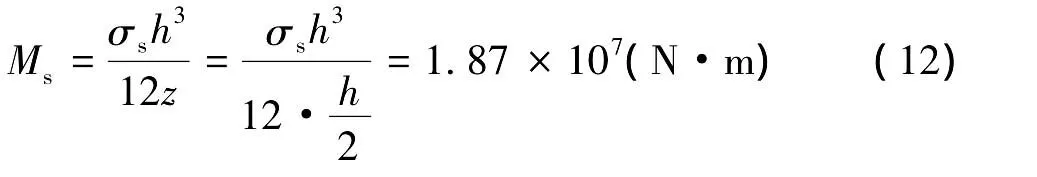
在此基础上，再将已知的顶板工作面长度和均布载荷分别代入表2中所示公式，便可求出不同边界条件下坚硬顶板的最小破断距。其最终结果用表3中的理论解列出。

为了验证理论解的正确性，此处选择通过数值模拟实验的方法［14］来寻求坚硬顶板的最小破断距。其具体的数值模拟过程为:坚硬顶板在均布载荷作用下，顶板的承载力会随着顶板结构的变化而变化。依据材料破坏的最大拉应力准则，当坚硬顶板所受应力超过顶板的极限应力时，顶板将会发生破坏。在数值模拟过程中，通过保证所建数值模型的长、高不变，而通过重复改变模型宽度的方法来寻求坚硬顶板的最小破断距。当确定一种边界条件下的坚硬顶板的最小破断距后，重新设定其他的边界条件，并按相同的方法来确定出相应的最小破断距。其完全模拟结果的数值解由表3列出。

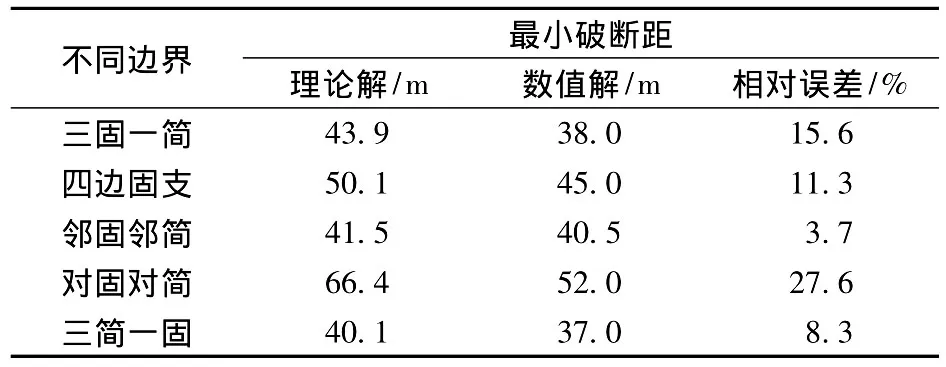
表3 顶板破断距的数值验证

从表3中可以发现，理论解均大于数值解，这主要是因为在理论求解过程中考虑了顶板的塑性极限作用。除顶板为对边固支和对边简支边界时，两者的相对误差较大之外，其余都在可接受范围内。因此，通过数值实验证明前文的理论求解是可行的。这可以为煤矿开采步距设计提供初始的理论参考依据。

4 主要结论

（1）利用塑性极限分析法得到采场坚硬顶板在不同边界下的极限载荷、最佳破坏机构的位置，并且得到了不同边界下坚硬顶板的最小破断距。此外，运用数值实验方法验证了理论解的正确性。这可以为顶板控制提供一定的理论依据。

（2）通过分析得出坚硬顶板极限载荷的如下规律:不同边界下顶板的极限载荷都随k值增大而减小，且在k＜0.25之前，顶板的极限载荷随k急剧变化，而在之后变化相对缓慢。此外，顶板极限载荷都在k=1.0附近趋于零，即顶板将失去承载能力。

（3）当顶板处于对边固支和对边简支边界时，顶板的极限载荷值最大，说明此类顶板具有更好的承载能力。所以在采矿中应尽量保持满足此类边界条件，以发挥顶板自身的承载作用。

［1］李彦强.顶板事故预防与处理［M］.徐州:中国矿业大学出版社，2009.

［2］岑传鸿.顶板灾害防治［M］.徐州:中国矿业大学出版社，1989.

［3］刘 洋，伍永平.近浅埋煤层开采顶板垮落步距分析 ［J］.煤矿开采，2009，14（6）:10－12.

［4］钱鸣高，石平五.矿山压力与岩层控制［M］.徐州:中国矿业大学出版社，2003.

［5］鹿志发.浅埋深煤层顶板力学结构与支架适应性研究［D］.北京:煤炭科学研究总院，2007.

［6］刘 俊.基于板模型的顶板力学分析及应用［D］.徐州:中国矿业大学，2008.

［7］谭云亮，蒋金泉.采场坚硬顶板断裂步距的极限分析 ［J］.山东矿业学院学报，1989，8（3）:21－26.

［8］何富连，赵计生，姚昌志.采场岩层控制论［M］.北京:冶金工业出版社，2009.

［9］钱鸣高，缪斜兴，徐家林，茅献彪.岩层控制的关键层理论［M］.徐州:中国矿业大学出版社，2000.

［10］［美］R.Szilard.板的理论和分析［M］.陈太平，戈鹤翔，周孝贤.北京:中国铁道出版社，1984.

［11］陈家瑾，范存新，谢小明.钢筋砼板极限分析的塑性铰线理论的改进［J］.苏州城建环保学院学报，2001，14（3）.

［12］钱鸣高，朱德仁，王作棠.老顶岩层断裂型式及其对工作面来压的影响［J］.中国矿业学院学报，1986（2）:9－18.

［13］钱鸣高，缪协兴，黎良杰.采场底板岩层破断规律的理论研究 ［J］.岩土工程学报，1995，17（6）:55－62.

［14］浦 海，黄耀光，陈荣华.采场底板X－O型断裂形态力学分析 ［J］.中国矿业大学学报，2011，40（6）:835－840.

Analysis of Roof Limit Load and Broken Pace under Different Boundary Conditions

HUANG Yao-guang，PU Hai
（1.State Key Laboratory of Deep Geomechanics and Underground Engineering，China University of Mining ＆ Technology，Xuzhou 221008，China;2.Mechanics＆ Architecture School，China University of Mining ＆ Technology，Xuzhou 221006，China）

Complex geological condition and different mining methods in coal mining will result in multi boundary condition of roof.Under different boundaries，limit load and broken pace of hard roof was different without fail.5 roof mechanics models with 5 different boundary conditions were set up.Roof limit load under different boundaries（4 sides fixed，3 sides fixed and 1 side simply supported，adjacent fixed and adjacent simply supported，opposite side fixed，3 sides simply supported and 1side fixed.）was obtained by plastic limit method.Variation rule of limit load with k（ratio of advance distance to mining face length）was analyzed.Roof limit load reached maximum under the condition of opposite side fixed and opposite side simply supported boundary.4 sides fixed boundary was secondary.Other 3 boundary conditions were almost equal.Minimum roof broken pace of every boundary condition was obtained on the basis of roof limit load，which was verified by numerical simulation.

different boundary condition;hard roof;limit load;broken pace

TD323

A

1006-6225（2012）02-0012-05

2011－12－26

国家自然科学青年基金 （50904065）;教育部新世纪优秀人才支持计划 （NCET－09－0728）;教育部博士点新教师基金（20090095120007）;江苏省高校“青蓝工程”资助;中国矿业大学中央高校基本科研业务费专项资金

黄耀光 （1985－），男，四川南充人，硕士研究生，主要从事岩石力学与采矿工程方面的研究。

［责任编辑:潘俊锋］