临床试验中多重性问题的统计学考虑
临床试验根据研究目的不同可分为“探索性临床试验”和“确证性临床试验”,而临床研究结论通常需要根据确证性临床试验的统计推断结果得到。如果某一确证性临床试验需要对多个检验假设做出统计学推断,例如多个主要疗效指标的多重检验、多组间多重比较、多个时间点的期中分析(interim analysis)等情况下,便会涉及多重性(multiplicity)问题。无须考虑多重性问题的临床试验一般限于下列情况:即单臂或双臂设计、使用单个主要指标、事先只指定了一个与主要指标相关的原假设且在一个时间点上进行统计推断。除此以外的其他情况理论上都应考虑多重性问题。在一个假设检验中,错误地拒绝原假设称为I类错误(type I error),I类错误概率通常用α表示。若进行统计推断时遇到多重性问题但未经妥善处理,则会导致I类错误增大。对确证性临床试验进行评价时,将I类错误控制在可接受的α水平上是一个重要的原则。所以在制定研究方案和进行统计分析时应慎重考虑统计推断的多重性及相关问题。多重性问题的定义、统计推断的原则以及控制I类错误的方法等关键点需在方案中事先详细阐述。
妥善处理多重性问题的意义
I类错误的增大,会导致将一个无效或劣效的药物有更大的机会推向市场,其后果是灾难性的。例如,在一项确证性临床试验中,设定了4项主要疗效指标,如果从这4个指标的统计分析结果中选择P值最小者来判断疗效,若每次假设检验均为单侧0.025的检验水平,那么4次检验至少出现1次假阳性结论的概率最高可接近10%(即1-0.9754),而不是研究者假定的2.5%。像这样在确证性研究中试图从多个检验结果中仅选择有利的部分结果,将大大增加发生假阳性错误的机会。因此,针对多重性问题就需要在方案设计时制定出有效的策略和方法来事先控制I类错误。
多重检验中I类错误的有关概念
假设同一项研究中的m个假设检验结果如表1所示。

表1 多重检验的结果
其中R是可观察到的随机变量,S、T、U、V均无法观察到,m和m0是固定数值,但m0大小未知。
将多个假设检验看做一个整体,其中至少有一次错误拒绝原假设,就会导致错误的决策,这一错误的概率称为总I类错误率(family-wise error rate,FWER):
FWER=P(V>0)
即m次检验中至少发生一次I类错误的概率。在确证性临床试验中所指的“控制I类错误”发生率,是强控制(in the strong sense)总I类错误率FWER,即在同一问题的多个假设检验中,应控制至少一个真的原假设被拒绝的概率在通常可接受的某个α水平即αFWER上,而不论多次检验中的哪个或哪些原假设为真;相应地在所有原假设为真的条件下控制总I类错误率FWER则属于弱控制(in the weak sense)。
强控制FWER常常意味着事先对αFWER进行分配,不同的原假设须在其分配所得到的校正后检验水平上进行检验。采用何种分配αFWER的算法视具体问题而定,相应的理论有简有繁,不同的选择可能会得出不同的结论,因此,必须在试验设计时事先指定校正方法,包括是否需要进行多重性校正的考虑,并详细介绍具体校正步骤。如果出现非预见的多重性问题,就必须使用保守的方法,例如Bonferroni法,当然此时会降低把握度。
常用的控制I类错误的方法
1.一般原则
(1)并-交检验与交-并检验
并-交检验(UIT,union-intersection test)意为:若对应于m次检验的基本原假设为H1,H2,…,Hm,相应备择假设表示为 K1,K2,…,Km。并-交检验是把上述各基本假设的交集HI作为全局的原假设,而把上述各备择假设的并集KU作为全局的备择假设,即检验:
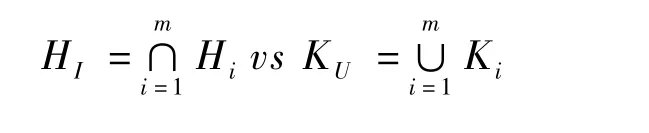
并-交检验中,只要有一次检验有统计学意义即可拒绝全局HI,故需要调整每次检验的水准以控制总I类错误。如果对某种疾病疗效的评价涉及多个方面问题,根据其中一个或多个(但不是全部)方面问题上的有利证据即可判定为药物开发成功,这样就可能带来从多重分析中选择有利结果的机会,需采用并-交检验考虑控制FWER的方法。
而交-并检验(IUT,intersection-union test)所定义的全局原假设HU是各基本原假设的并集,全局备择假设KI定义为各备择假设的交集,即检验:

交-并检验中当每个假设Hi均被拒绝时,才可拒绝全局原假设HU。如果一项临床试验中所有的多个主要指标同时都需要有统计学意义才可认为疗效有临床意义,则需采用交-并检验。例如预防宫颈癌有针对HPV(人乳头状瘤病毒)16、18、6、11 型的四价疫苗,其疗效评价指标是针对上述四种分型来评价其各自免疫原性的抗体滴度。无论哪一个分型的免疫原性没有统计学意义,原假设HU就不被拒绝(疫苗的有效性就不会被法规部门认可),或者说只有四个指标均有统计学意义时才可拒绝原假设,此时由于没有机会选择四项指标中最有利的单次假设检验结果,因此无需进行多重性校正。
实际工作中的多重检验往往是并-交检验、交-并检验或其组合。图1、图2分别为二者的示意图,其拒绝全局原假设的条件非常类似于物理学上的并联和串联电路。

图1 并-交检验
图2 交-并检验
(2)闭合原理与分割原理
如何确定前述并-交检验拒绝HI时哪个(些)基本原假设不成立,可采用闭合原理(closure principle)构建逐步法来进行分析。1976年Marcus等人提出的这种多重检验构造方法,能灵活地把各种研究目的之间的关系和重要性综合反映到一个恰当的多重检验步骤中,基于此原理构造出的多重比较方法称为闭合检验(closed test procedures)。很多常见的多重比较方法实际上都可视为某种闭合检验,如Holm、Shaffer、固定顺序检验法等。闭合原理的缺点是难以构造相应参数的联合可信区间。
例如以下的最简单情形:两个主要指标在两组间比较,设 θi=μiT- μiC为感兴趣参数,i=1,2 分别表示两个指标,μt、μc分别表示处理组与对照组的总体均数。这里的基本原假设为 Hi:θi≤0,i=1,2。如果采用Bonferroni检验,为把总I类错误率控制在α水平,可对每个基本原假设Hi在α/2水平进行检验。但运用闭合原理即可以得到把握度高于Bonferroni的检验。形式上可以把Hi看作要进行推断的参数空间的子集。令Θ=ℝ2表示具有参数θ=(θ1,θ2)∈Θ的参数空间。图3显示原假设Hi={θ∈ℝ2:θi≤0},i=1,2是实平面(参数空间)的子集。显然,两个基本原假设H1和H2相交,两者的交集为H12=H1∩H2={θ∈ℝ2:θ1≤0,θ2≤0},就是图 3中的第 3象限。检验交集H12需要多重性调整。假如考虑采用Bonferroni检验来调整,这个方法实际上是在α/2水平检验整个并集H1∪H2,而不仅仅是检验交集H12。图3也表明剩下的2、4象限部分均能在α水平进行检验,不需要进行进一步的多重性调整。由此得到如下自然的检验策略:首先采用适当的并-交检验以检验交集H12,如果H12在第一步没有被拒绝,则无需对H1或H2作进一步检验即可认为H1和H2均不能被拒绝;如果H12有意义,那么继续在全局α水平检验H1和H2,当且仅当H1和H12均在(局部)α水平被拒绝,才可认为H1可被拒绝,对H2亦然。
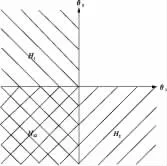
图3 参数空间ℝ2中两个假设H1和H2及其交集H12
对于更一般的情况,闭合检验也同样首先对基本假设Hi的所有交集采用适当的校正检验水平进行并-交检验,当且仅当包含基本假设Hi的所有交集有统计学意义时再逐级向上直至最后对基本假设Hi采用全局α作检验,若包含基本假设Hi的交集在校正的检验水平上无统计学意义,则无需对含有Hi的假设做进一步检验。
分割原理(partitioning principle)最先由Finner和Strassburger(2002)正式提出,基本想法是把感兴趣的参数所对应的基本假设Hi的并集分割成不相交的若干个参数空间的子集,由于这些子集互不相交,所以其中最多只有一个子集对应的假设为真,这样对每个子集的检验只需在α水平上进行即可控制FWER。其优点是可构造出比闭合检验把握度更高的方法且便于得到相应参数的联合可信区间。
仍以两指标两组比较为例,令 θi=μiT- μiC,i=1,2为感兴趣的参数,再令Θ=ℝ2表示具有参数θ=(θ1,θ2)∈Θ 的参数空间。基本原假设为 Hi={θ∈ℝ2:θi≤0},i=1,2。Ki表示相应的备择假设。图 3显示基本原假设H1和H2是实平面(参数空间)的子集。现在把参数空间Θ分解为如下集合:Θ1=H1,Θ2=H2∩K1,Θ3=K1∩K2,见图 4。因为 Θi,i=1,2,3 不相交,且Θ1∪Θ2∪Θ3=Θ,因此,它们构成参数空间Θ的一个分割。这样,真实的参数向量θ在且仅在互不相交的子集Θi中的某一个集合里。因此,对这些子集采用(局部)α水平检验就是一个多重检验,这个检验把总I类错误严格控制在了α水平。另外,参数向量θ的可信集就是被拒绝的假设的补集之交集。

图4 两个原假设H1和H2的分割原理
2.常见多重比较方法
根据对检验顺序是否有要求,多重性校正方法可分为单步法和逐步法。单步法对每个检验是否拒绝原假设的结论均不依赖于其他各次检验,也就是说各个检验的顺序并不重要,可同时进行所有的检验。例如Bonferroni和Dunnett检验。而逐步法是按照一定顺序依次对相应原假设进行检验的,这些顺序上的安排使得其中一些原假设被隐含在其他假设中,从而有可能进行一次检验就能对多个假设下结论。逐步法又分为向上法和向下法。向上法是从P值最大的假设开始检验,若结果无统计学意义,则对P值次大的假设进行检验,若结果有统计学意义,则宣布该假设及之后的所有假设均具有统计学意义,如Hochberg方法。向下法的检验顺序则相反,它首先从P值最小的假设开始检验,若结果有统计学意义,则对P值次小的假设进行检验,若结果无统计学意义,则宣布该假设及之后的所有假设均具无统计学意义,如Holm方法。一般而言,单步法的把握度会低于相应逐步法,但前者的优点是其联合可信区间构造相对简单。
根据对分布假设的要求,多重性校正方法可分为3类:其一是基于P值的方法或非参数方法。这类方法不指定检验统计量的联合分布,只依据单变量的P值来进行检验,如Bonferroni和Holm方法。在检验次数很多或检验统计量之间有很强的相关时这类方法把握度较低,结论偏保守。其二是参数方法,如指定了统计量服从多元正态分布或多元t分布时的Dunnett检验等。其三是基于再抽样的方法,通常是通过bootstrap再抽样法或permutation检验来近似统计量的联合分布。后两种方法在进行多重性校正时考虑了多个检验间的相关性。多个指标相互独立时,FWER增大得最严重,相关性高,FWER增大程度减少。
为节省篇幅,将一些常见多重比较方法列于表2,有兴趣的读者可参阅相关文献。

表2 常见的一些多重比较方法
常见的多重性问题及处理方法
以下主要针对多个主要疗效指标和多组间比较的情况作一介绍,多个时间点的期中分析将作为专题另作讨论。
1.多个主要指标
需要指出,当事先指定了一个主要指标和多个次要指标,且声明所有次要指标属于支持性证据的情况下,由于结果的判断主要取决于单个主要指标,故不存在从多次比较中选择有利结果的机会,不需要考虑多重性校正。
(1)所有的多个主要指标同样都需要有统计学意义才可下推断结论时,属于交-并检验。此时由于没有意图或机会选择最有利的某次假设检验结果,因此可设定每次检验的I类错误水平等于αFWER,无需进行多重性校正。但应注意此时会增大II类错误(错误地不拒绝至少1个原假设),在估算试验的样本量时应设定较高的把握度。把握度的损失除了与指标多少有关,还受到指标间相关性的影响。若相互独立,其把握度为单个指标把握度的乘积,若完全相关且标准化的效应值相同(实际上很难发生),则不增大II类错误。
(2)假设有m≥2个主要指标,至少有一个达到有统计学意义即可认为药物有效的情况下,由于存在从多次比较中选择有利结果的机会,故需要考虑多重性校正来构建并-交检验。如前述基于Bonferroni类和Simes类的各种方法。
(3)同一个试验中多个疗效指标可能具有不同的重要性,其中一个指标最为重要,而其他指标如果出现令人信服的结果也将明显提升试验品的价值。此时原假设可以按照分级的策略进行检验。分级的次序可以是自然的次序(例如假设按时间或指标的重要程度排序),也可以根据研究者具体的关注点。检验原假设的等级次序应当在方案中事先说明。如果多个主要指标存在上述层次结构从而决定了其假设检验的顺序,只有在位次靠前的检验有统计学意义时才可进行下一个检验,此时不需要校正I类错误,每次检验的水准均等于αFWER。这是由于每次检验的拒绝域总是落在上一次大小已设定为αFWER的拒绝域之内,故而这种固定顺序的序贯检验的I类错误不会超过第一次检验所设定的αFWER,但是对应较低等级指标的假设检验的II类错误将增大。需要注意的是,一旦依次进行的某个原假设没有被拒绝,该序贯检验终止,本次及之后的所有检验均认定为无统计学意义。例如E1、E2、E3三个指标依次被检验,指标E2没有统计学意义,那么E2和E3所指向的临床价值就不能被肯定(无论指标E3是否有统计学意义)。这一策略典型地体现于主要指标和次要指标共存时的假设检验,亦即当主要指标没有统计学意义时就不能根据次要指标的检验结果推断药物疗效。
(4)设有三个主要指标E1,E2和E3,当E1单独有统计学意义或者E2和E3同时有统计学意义即可认为药物有效。全局原假设可写为HE1∩{HE2∪HE3}。这种情况下的原假设实际上是另外两个原假设的交集,其一是E1无效,其二是E2和E3至少有一个无效。对这两个原假设的交集可采用Bonferroni类方法来控制FWER,即首先在小一点的α1水平检验E1,之后再用剩余的α-α1水平检验E2和E3中的每一个。
(5)设有三个主要指标 E1,E2和 E3,当 E1和 E2同时有统计学意义或者E1和E3同时有统计学意义即可认为药物有效。全局原假设可写为{HE1∪HE2}∩{HE1∪HE3}。这种情况相当于(E1,E2)和(E1,E3)的交集作为了临床决策依据。此时E1是临床收益方面最有关的指标,但仅这一个指标尚不能足以说明临床疗效,还需要E2或E3中至少一个也有统计学意义。这样E1和E2、E3的交集就存在一种分级次序:如果E1没有被拒绝就无需检验E2和E3。故而可以首先对E1在整个α水平上作检验,如果被拒绝,接着再对E2和E3采用在α水平上控制FWER的方法做并-交检验。
2.多组比较
(1)多剂量组与对照组相比
若剂量组间无效应大小顺序限制,可采用Dunnett及其逐步法;如剂量组间效应已确认有大小顺序限制(如随着剂量增加效应值单调上升),可采用固定顺序的检验方法,此时无需调整I类错误。
(2)多个剂量组相比,无安慰剂和阳性对照
通常是由于伦理方面的考虑不设安慰剂且没有合适的阳性药物。高剂量组的耐受性和低剂量组的疗效可能会不满足要求,而某个较高剂量组可能安全有效。可在全局性假设检验的基础上进行有I类错误控制的多重比较,如进行所有两两比较所采用的Shaffer方法等。
(3)试验药、阳性对照和安慰剂比较
当符合伦理要求时常常建议采用如下三个组的设计来证明新药的疗效和安全性:试验药、阳性对照和安慰剂。通常这种研究的目的有多个:①验证试验药与安慰剂相比的优效性(确证疗效);②验证阳性对照药与安慰剂相比的优效性(证明试验的灵敏度);③验证试验药非劣于阳性对照药(证明非劣效性)。如果这三个目的要同时达到,即要求所有这3个假设检验都必须在所需的检验水平显示有统计学意义,可进行交-并检验而不需要校正I类错误。此时,如果未能显示试验药优于安慰剂,就可解释为试验药无效(当阳性对照药优于安慰剂时),或试验缺乏灵敏度(当试验药和阳性对照药未显示优于安慰剂)。
复合指标
多个指标均有统计学意义时才能判断药物有效则通常进行交-并检验而不考虑对I类错误的校正,故而在多个指标均有统计学意义而其临床意义并不是很明显的时候常常会考虑将临床上既往经验证握与治疗效果有关的多个指标构造成一个单独的复合指标来避免多重性问题。复合指标的类型有2种。第一种即等级评定量表,它是由多个反应不同侧面治疗效果的临床指标合并而产生。这种类型的复合指标在某些适应证(例如精神或神经系统疾病)中有长期的使用经验。另一种类型的复合指标是在生存分析的背景下产生的。可以综合几个事件来定义复合指标。定义复合指标最好是把所有较为重要的临床事件都作为构成指标。如果患者出现事先指定的构成指标(例如死亡、或心肌梗死,或致残性卒中)列表中的一个或多个事件,则认为患者有这种临床结果。至出现结果的时间以患者随机化至首次出现列表中事件的时间计算。通常,各构成指标代表相对罕见的事件,并且单独研究每个构成指标需要非常大的样本量。此时,使用复合指标旨在增加达到预期的事件数,从而可以提高研究的把握度。除主要指标外建议还要分别分析单个构成指标以提供支持性信息。当主要指标有统计学意义,则对单个构成指标的检验无需进行多重性校正。如果宣称的疗效是基于复合指标中某个或某些成分时,则需事先定义这些成分并纳入包括多重性考虑的确证性分析策略。
定义复合指标时,建议各构成成分仅采用以同样的方式受到预期治疗影响的指标。所有构成成分都应该能够反应好的治疗效果,或者临床上更为重要的成分至少不能出现负面的疗效,增加一个可以预见的对治疗作用不敏感的构成指标会导致变异性增大,其直接的后果将是降低灵敏度。非劣效性或等效性研究中也应避免指标的变异性增大。对于目的是为了证明优效性的研究,首选较为一般性的构成指标作为主要指标,因为这是最保守的分析。由于同样原因,对于非劣效性/等效性试验,首选更特殊的构成指标(例如疾病相关的病死率)作为主要指标。
常见问题问答
(1)是否有多个主要疗效指标的情况进行统计推断时就要进行多重性校正?
答:对多重性的考虑是必要的。但是否要进行多重性校正要视具体情况,例如如果多个指标同时有统计学意义才可以判断试验品有效,则无需进行多重性校正。
(2)是否多个剂量组比较就要考虑统计推断时进行多重性校正?
答:对多重性的考虑是必要的。但是否要进行多重性校正要视具体情况,例如多个剂量组的剂量组间效应已确认有大小顺序限制(如随着剂量增加效应值单调上升),可采用固定顺序的检验方法,此时无需调整I类错误。
(3)如何决定多个主要疗效指标应采用并-交检验还是交-并检验?
答:单纯的交-并检验不需要多重性校正,而并-交检验要考虑多重性校正,所以存在多个主要疗效指标时确定哪种类型的检验较为重要。而检验类型的确定与试验品本身的药效特点有关,为明确检验类型,临床专家在方案中要明确描述出多个指标同时有意义还是多个指标中任意几个有意义或者多个指标的某几种组合有意义表示试验品有效,这样才能明确定义出检验类型。
(4)同一指标在多个数据集中进行假设检验,是否要考虑多重性校正?
答:不需要考虑。对不同的个体分属何种数据集(FAS或PPS)在研究方案和统计分析计划中须明确定义,从中选择一个(通常是FAS)作为主要的分析集。一般而言,对受试者不同子集进行多重分析是用于分析主要结论的敏感性,增加从主要分析集所得结果的可靠性,不需要校正I类错误。
(5)对于相同的数据集使用不同的统计学模型作多次检验是否需考虑多重性校正?
答:对于相同的数据集,有时会使用不同的统计学模型或2步法,目的是为了选择恰当的统计学方法,在第一个统计学检验结果的基础上进行主要疗效的比较(如首先在正态性检验的基础上决定其后采用t检验或者秩和检验)。如果这些方法提供有明显的机会,使得根据已知的患者治疗分组情况可选择有利于结论的分析策略时,则会立即产生对多重性的顾虑。虽然技术上而言对同一数据用不同的统计方法需要考虑分配总I类错误,但若基于正式的盲态核查(见ICH E9)而选择的最终统计学模型则不会出现这些顾虑,而且主要的统计分析策略应在统计分析计划中提前说明,并在随机化治疗分配信息公开之前确定。即使是使用了不同的统计方法,通常也是为说明研究的可靠性和结果的稳健性。类似的问题可存在于协方差分析或其他多因素模型中,须纳入模型的变量和分析策略需要在方案中事先说明才可用于疗效的确证性研究。
(6)多个剂量组的设计,建立了剂量-反应关系,是否均需考虑多重性校正?
答:有时一项研究没有足够的把握度来发现和推荐单个有效和安全的剂量(或剂量范围),但可以成功地确证总体上临床作用与剂量增加呈正相关。此时可以按外推的方式将组间比较的估计值和可信区间用于设计将来的研究,或者分析目的是为了探索剂量-反应关系模型,在这种情况下,没有必要调整I类错误。
(7)对实验室安全性数据或不良反应的分析是否需要多重性校正?
答:安全性数据分析主要通过列表来进行描述,但如果某个安全性指标在整个研究中要作为确证性策略的一个部分,如欲声称所研究药物可以增效减毒,那么此安全性指标就应和主要疗效指标同样对待,统计分析策略中应考虑所涉及的多重性问题。不良反应的分析中率差或风险比等描述严重性程度的指标,以及相应的可信区间,通常要比假设检验的P值更为重要,而且由于是否发生特定的不良反应是难以在制定方案时事先预设的,其假设检验也就难以事先明确定义,故而其重要性通常是依据已掌握的关于此药物的药理学知识来决定。同时,由于通常的研究设计(包括样本量的估计)不是针对不良反应的,对不良反应进行统计学推断的样本量往往达不到一定的把握度,因此,其假设检验结果也只有参考价值。除非观察某种不良反应是研究的主要目标,针对不良反应的假设检验无需调整检验水准。
(8)多次访视的结果在不同时间点比较是否需要进行多重性校正?
答:在多次访视时,由于对主要疗效的评价通常是在事先指定的某个访视点或按照方案中的治疗终点进行,此时一般不考虑类似重复测量分析的潜在多重性问题。
(9)双单侧等效性检验是否应考虑多重性校正?
答:等效性检验是一种典型的交-并检验,因为只有两次单侧检验都具有统计学意义时才可以认为等效性结论成立,所以两次单侧检验都不需要校正检验水准。
(10)亚组分析是否应考虑多重性校正?
答:如果研究目的中特别声称特定亚组的治疗作用,研究计划中就要事先指定相应的原假设和妥善的确证性分析策略,其中包括对多重性问题的考虑。许多研究中,当达到主要目标后,亚组分析具有支持性或探索性目的,即证明显著的总体临床受益。当总的研究人群中疗效未被证实,基于亚组分析的疗效推断结论被接受的可能性极小。需要注意的是,无计划的亚组分析有时会形成错误的进一步研究假设;而无法事先明确假设检验的次数有时也难以控制总I类错误;使用随机化之后测量的某个变量分组会形成不恰当的亚组,例如这样的亚组中排除了试验失败者。而恰当的亚组是根据随机化之前测量的基线指标形成,如人口学特征或预后有关变量等。事先的计划是任何亚组分析的关键点。除了可能的多重性问题,方案中应当考虑到把握度,随机化一般应当分层。
1.Committee for Proprietary Medicinal Products(CPMP).Points to Consider on Multiplicity issues in clinical trials.http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500003640.pdf
2.ICH.ICH Topic E9:Notes for Guidance on Statistical Principles for Clinical Trials,International Conference on Harmonization,London.http://www.emea.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500002928.pdf
3.Alex Dmitrienko,Ajit C.Tamhane,Frank Bretz.Multiple testing problems in pharmaceutical statistics.Chapman & Hall,CRC Press,2010.
4.Frank Bretz,Torsten Hothorn,Peter Westfall.Multiple comparisons using R.Chapman & Hall,CRC Press,2010.
5.Marcus R,Peritz E,Gabriel KR.On closed testing procedures with special reference to ordered analysis of variance.Biometrika,1976,63,655-660.
6.Finner H,Strassburger K.The partitioning principle:A powerful tool in multiple decision theory.The Annals of Statistics,2002,30:1194-1213.

