非线性半相依回归模型在生长曲线研究中的应用*

山西医科大学公共卫生学院(030001) 赵俊康 梁洪川 王 彤

半相依回归(seemingly unrelated regression，SUR)也称为相依回归或似乎不相关回归，可视为多个因变量情形下多元回归(multivariate regression)的特例，由于它允许方程组中多个方程存在不同的自变量，这就为统计建模带来了较大的灵活性。同时，SUR在参数估计过程中考虑了方程间的相关信息，使参数估计效率在满足某些适当条件下较之对每个方程分别作最小二乘估计的传统方法得到改进〔1〕。

该方法最早源于计量经济学实践，回归方程组被用于解释不同的经济实体或同一经济实体不同时期经济活动中各要素的相互作用规律，作为多元线性回归模型的自然扩展，Zellner首次提出此模型用来解释通用电气和西武公司固定资产投资总额与其已发行股数额和现实资本额的关系，使用了半相依回归这个名称，并提出了两步估计法(two－stage estimator)。自Zellner的建设性工作后，SUR“在现代计量经济学中扮演了中心角色”〔2〕，并且在经济、工业、地质和社会科学等领域得到广泛应用，在医学领域也有很大的应用前景。我国学者有王松桂、陈桂景等提出协方差改进估计用于该模型〔3－4〕。

医学研究中很多现象是属于非线性的，如血药浓度与时间变量的关系等。模型的非线性有两种可能的情况，一种是因变量与自变量的非线性，此类模型大多可通过合适的变换化为线性模型，只要变换后误差仍为可加，则线性模型的估计理论和方法都适用。另一种是因变量与参数的非线性，这种情况下非线性是内在的，无法变换为线性模型，此时必须采用新的参数估计方法。

原理与方法

1.模型结构

非线性半相依回归模型可写为

xti是(ki×1)向量，代表第i个方程、第t个观测中的自变量值;θi是参数空间中第i个方程的未知参数向量;fi(·;·)为第i个方程的非线性函数;e=(et1，et2，…，etm)'被假定为相互独立同分布，均值为零，方差－协方差为∑的误差向量〔5〕。

2.参数估计

非线性半相依回归模型的参数估计思想与线性模型类似〔6〕。

首先，不考虑方程间相关信息，我们对每一非线性方程极小化目标函数

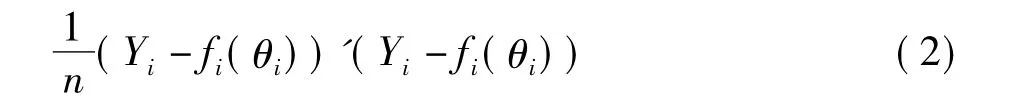
得到各方程的非线性普通最小二乘估计，如果误差向量为正态分布，则此估计还是极大似然估计。

然后，误差向量的方差－协方差矩阵可估计为以

为元素的矩阵s=((sij))，得到∑的一致估计∑∧。

最后，考虑方程间的相关信息，在参数空间Θ上极小化目标函数

从而得到非线性半相依回归参数^θ的FGLS估计。

极小化目标函数的方法可采用 Gauss－Newton、Newton－Raphson和极大似然估计等非线性模型的估计方法。Gallant提出了一种将多元问题转换为一元问题的解决方案。Gallant建议将作Cholesky分解，即令=H'H，然后令 Z=YH'，d(θ)=f(θ)H'，则目标函数变为

Gallant的方法使得原有得一元非线性程序只需稍微改动即可应用于多元模型。

Gallant证明，如果方程间确实有相关关系，且各方程的自变量xti不均相同，并且每一方程的非线性函数fi(xti;θi)形式不同，则非线性半相依回归优于非线性普通最小二乘回归。反之，如果模型中每一个方程的自变量xti都相同，并且每一方程的非线性函数fi(xti;θi)有相同的形式，则非线性半相依回归与非线性普通最小二乘参数估计结果相同，即^θ(I)与^θ(∑)有相同的渐近分布。

3.假设检验

由于非线性模型参数无显解式，其估计的小样本分布很难导出，但Gallant，Willlam得到了一些大样本性质〔7〕。Gallant证明当∑∧为∑的一致估计时，非线性半相依回归参数^θ的FGLS估计服从渐近正态分布

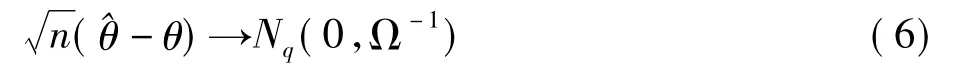
其渐近方差－协方差阵为

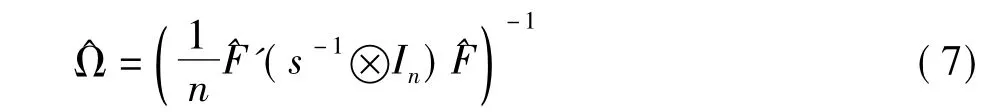
其中

如误差向量为正态分布，则FGLS还是极大似然估计。

由于以上的结果，线性模型的参数检验方法可在渐近理论的框架内移植。如Wald检验

4.S型剂量—反应关系曲线的非线性生长曲线分析模型

药物的剂量—反应关系分析是药理及毒理学试验的重要内容，其中重复测量设计是常用的试验设计方法。采用重复测量设计我们除了可以探讨不同试验条件对反应量的影响，还可同时了解反应量随时间变化特点和规律。在重复测量分析中，有时我们可以建立一个数学模型，用时间的函数来预测反应变量随时间变化趋势，这种分析方法称为生长曲线分析(growth curve analysis)。生长曲线分析可以采用多项式回归模型分析(polynomial regression model)、Rao－Khatri降维分析等线性模型方法。但线性模型只是生长曲线族中的特例，更多的是曲线生长的形式，如S型曲线等。这种情况下，使用线性模型方法可能无法很好的拟合资料。此时，应该用非线性方法拟合模型。

VØlund〔8〕提出了一种拟合 S型剂量—反应关系曲线的非线性模型，其形式为

Yij=1/［1+exp( － (A'iθXj))］+ δij(10)其中，i=1，2，…，n;j=1，2，…，m，Yij为第 j时点第 i个体的反应变量观测值，通常以百分率表示，反映某反应量占总反应量的百分比;Aj为第j时点的设计矩阵;θ为未知参数矩阵，我们一般假定参数向量不随时间改变，即各时点对应的参数向量相同。为此，我们可以对各时点方程的参数实施限制，使得各方程对应参数相等;Xj=(1，t'j)'，tj为第j时点。从模型的形式上看，由于每一方程j的自变量代表各自重复测量时点，即各方程自变量不相同，并且，各重复测量值之间大多存在相关性，所以该模型为非线性半相依回归模型，我们可在半相依回归的框架下，运用模型误差向量的方差－协方差矩阵信息，以提高模型参数的估计效率〔2〕。

实例分析

一项毒理学试验研究四氯化碳CCl4肝细胞毒性的剂量－反应关系及其与时间的关系。取64份肝细胞悬浊液，随机分为4组，分别加入剂量为0、1.0、2.5和5.0mM 的 CCl4，在加入后第 0、0.01、0.25、0.5、1、2、3小时测量乳酸脱氢酶渗出百分比。

图1 不同CCl4浓度在各时间点的平均乳酸脱氢酶渗出率曲线

以时间为X轴，乳酸脱氢酶渗出率为Y轴，绘出不同CCl4浓度在各时间点的平均乳酸脱氢酶渗出率曲线(见图1)，可见乳酸脱氢酶渗出率随时间变化呈非线性关系，可用非线性模型拟合数据。

将非线性回归方程写成通常的形式

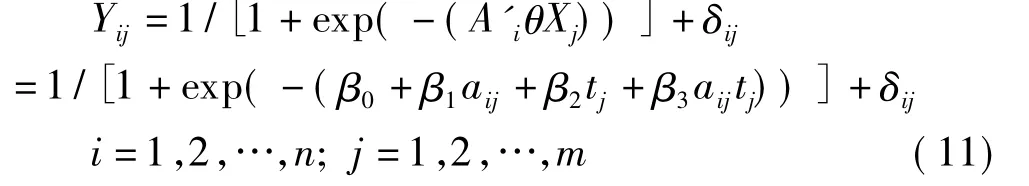
其中β0代表平均效应参数，β1表示CCl4的效应参数，β2表示时间的效应参数，β3表示CCl4与时间交互效应参数。

对此例拟合上述非线性半相依回归模型的参数估计结果见表1。

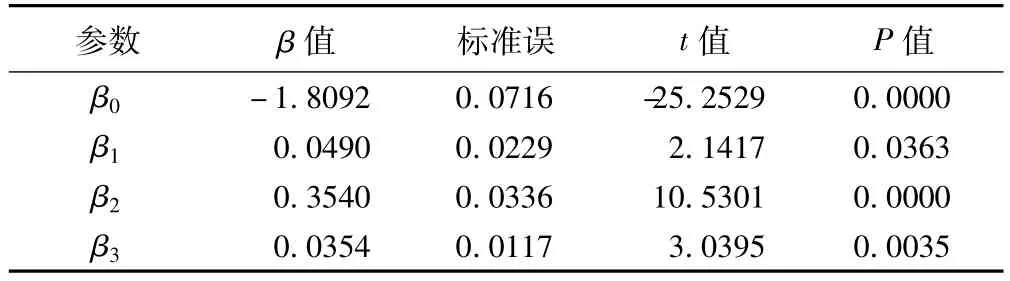
表1 非线性半相依回归拟合参数估计值及假设检验结果

可见，各估计参数的P值均小于0.05，说明CCl4及时间对乳脱酸氢酶渗出率的影响有统计学意义，CCl4与时间之间存在交互作用。最终模型可写为:

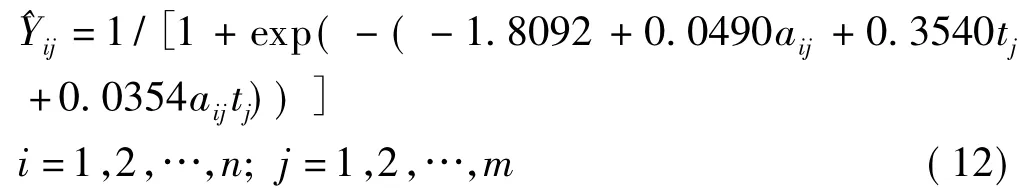
运用该模型，可以预测不同CCl4浓度在各时间点乳酸脱氢酶渗出率。

在本例中，由于我们需要对各个非线性方程对应的参数进行限制，令其不随时间改变而改变，所以无法对各个方程分别采用非线性普通最小二乘估计而获得统一的估计参数，我们必须在方程组框架下，才能对参数实施限制。这充分说明了半相依回归模型在建模上的特点。

讨 论

本文介绍了非线性半相依回归模型的参数估计方法及其大样本性质，指出方程间确实有相关关系，且各方程的自变量xti不均相同，每一方程的非线性函数fi(xti;θi)形式不同的情况下，非线性半相依回归优于普通非线性最小二乘回归。在医学研究中的生长曲线问题通常为重复测量设计，各重复测量值之间大多存在相关性，且在方程组形式中，若每一方程自变量Xj代表各自重复测量时点，即各方程自变量不相同，这些特点非常符合半相依回归系统的框架。故而此时运用模型误差向量的方差－协方差矩阵信息可提高参数的估计效率。同时，在通常的统计软件如SAS中，对重复测量的时间点之间建模仅提供多次项拟合，并不能满足更复杂灵活的非线性模型形式，而在非线性半相依回归框架下可以针对专业特点自行定义更利于专业解释的各种非线性函数来建模，较之于一般的重复测量方差分析具有不可比拟的灵活性。如药理和毒理学研究中各种剂量－反应关系通常是一个S型曲线，此时即可进行非线性半相依回归建模。

需注意的是，本文介绍的参数估计方法在因变量为多元离散分布或模型中包含更复杂的非参数项时，此方法将不再适用。关于广义线性模型或广义可加模型(generalized additive model)与半相依回归的结合，将另文介绍。

1.梁洪川，韩宏，郎素萍，等.似乎不相关回归模型及其在老年认知问题中的应用.中国卫生统计，2005，22(6):362－364.

2.Arthur Stanley Goldberger.A course in econometrics.Cambridge，MA:Harvard University Press，1991:323.

3.马铁丰，王松桂.两个半相依模型回归系数的改进估计.应用概率统计，2009，25(6):619－631.

4.王立春，汪惠民，陈桂景.一般半相依回归系统的协方差改进估计.应用概率统计，2001，17(2):156－162.

5.Judge，Hill，Griffiths，et al.Introduction to the theory and practice of econometrics.2nd ed.New York:John Wiley ＆ Sons，Inc，1988.

6.Gallant AR.Seemingly unrelated nonlinear regressions.Journal of Econometrics，1975，3:35－50.

7.Barnett WA.Maximum Likelihood and Iterated Aitken Estimation of Nonlinear Systems of Equations.Journal of the American Statistical Association，1976，71:354－360.

8.Aage Vφlund.Application of the four－parameter logistic model to bioassay:comparison with slope ratio and parallel line models.Biometrics，1978，34(3):357－365.