类别变量的结构方程模型及其应用*

王 欢 韩 海 蔡绍晖 梁 巧 吴肖蒙 王波栋 张志敏 柳士顺

与建立在连续变量基础之上的结构方程模型不同，类别变量的结构方程模型(structural equation model with categorical observed variables)中均值、方差和协方差变得没有意义。如果仍然运用以积差相关系数矩阵为基础的分析方法，就会导致不正确的结果和无效的结论，因此，对类别变量的结构方程模型的分析需要完全不同的统计技术来完成。

类别变量结构方程模型的分析方法

结构方程模型又称为协方差结构分析(covariance structure analysis)，其基本思想就是用样本的方差－协方差矩阵(以下简称协方差矩阵)去拟合根据研究假设推导出的协方差矩阵。可见，协方差矩阵是结构方程模型的分析基础。类别变量结构方程模型是基于多项相关系数的协方差矩阵。模型的参数估计方法使用加权最小二乘法〔1〕。

1.多项相关系数与渐近协方差矩阵

任何类别都有一个分类原则，在进行类别变量的结构方程模型分析时，类别变量的分类假设如下:

如果类别变量 x包含 k类，分别记为:1，2，．．．k，假设存在一个作为分类基准的潜在连续变量x*则有:

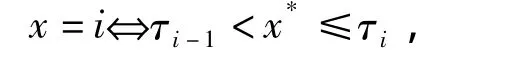
其中 i=1，2，…k;

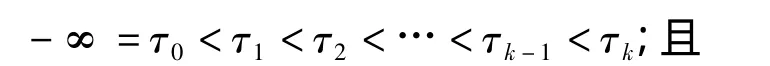
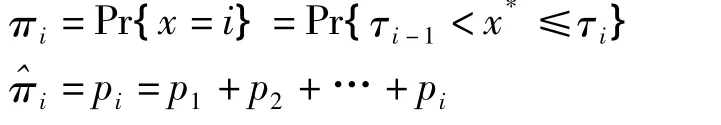
同样地，对于类别变量y来讲，也做类似的假设，即以潜在连续变量y*作为分类基准。为方便起见，假设x*与y*服从二元正态分布，则可通过极大似然估计法，估计出x*与y*的积差相关系数，此种相关系数就是多项相关系数(polychoric correlation);当x与y均为二分变量时，此种相关系数就是四项相关系数(tetrachoric correlation)。以多项相关系数为基础估计出的多个类别变量的协方差矩阵就是估计的渐进协方差矩阵(estimated asymptotic covariance matrix)，即类别变量结构方程模型的分析矩阵。

2.模型的参数估计

结构方程模型的分析原理主要是通过协方差矩阵的分析导出选定的参数，并对模型的拟合情况进行评价。由于校正加权矩阵(correct weight matrix)可以成为渐进协方差矩阵的一致估计，因此，对基于渐进协方差矩阵的结构方程进行分析时，采用的是加权最小二乘法(weighted least squares)〔2〕。加权最小二乘法要求样本量要大，缺失值要少。

应用实例

焦虑和抑郁是两种常见的精神障碍，对个人和社会带来了负担，是现代社会不可忽视的健康问题〔3〕。目前，对生活方式与抑郁和焦虑之间关系的研究还比较少〔4〕，日本学者以中老年为对象探讨了生活方式对抑郁的预测作用〔5〕。本研究以广东、上海、河南、浙江等省市机关和企事业单位的在职人员为对象，采用问卷调查法，发放问卷600份，回收有效问卷452份。其中，男性占64.8%;25岁以下的占17.7%，26岁至35岁占52.6%，36至45占24.2%，45岁以上占5.5%;研究生及以上学历的占4.7%，本科占26.4%，大专占31.3%，大专以下占10.6%。生活方式的测量工具是由Belloc和 Breslow开发，经Morimoto等人修订的包含八个项目的量表〔6－8〕;对抑郁与焦虑的测评使用的是Lowe等人所提炼的自陈式量表〔3〕;具体内容见表1。问卷的引导语为“根据近四个星期的情况，针对下列描述，选择最能反映您实际状况的答案”。LS3、LS6、DEP1、DEP2、ANX1 和 ANX2 为反向记分，其他各项目均按各自的等级从高到低记分。例如:“是否吃早餐”的记分为:0－1－2;“锻炼身体”的记分为:1－0;“无节制地饮酒”的记分为:2－1－0。

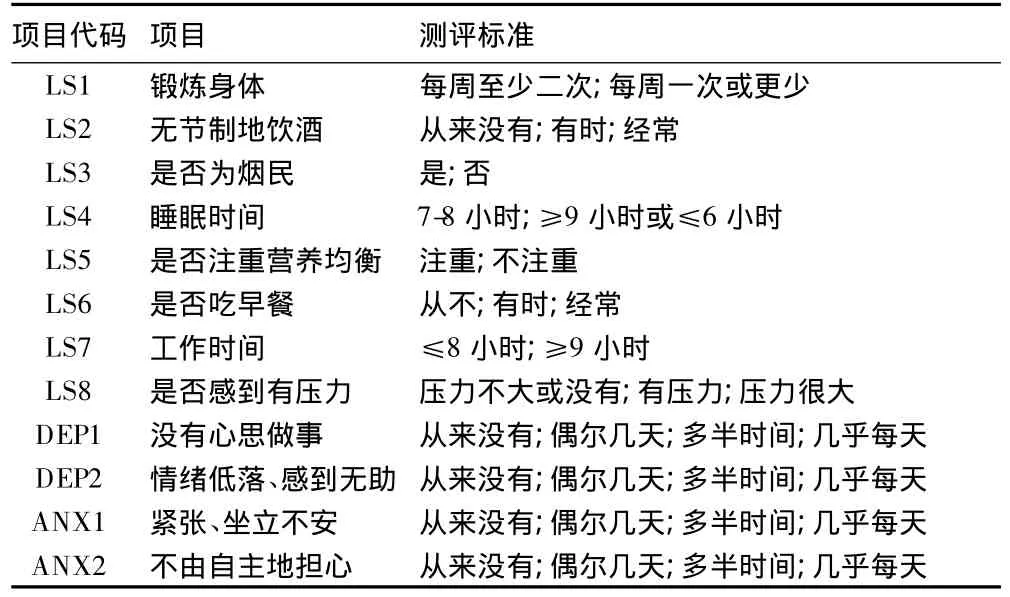
表1 生活方式与抑郁和焦虑的测评量表

数据处理方法与分析结果

本研究选用Lisrel 8.7对所取得的数据进行了处理分析。首先，读取数据，进入“PRELIS”界面，按照“Data－Define Variables”定义变量，通过“Statistics－Output Options－Moment Matrix;Asymptotic Covariance Matrix”可得到各个变量的临界值、相关系数矩阵和渐近协方差矩阵及其检验结果。本研究的卡方检验和接近拟合(close fit)均达到良好水平。

接着，对假设模型进行检验，检验程序如下:

HEALTH ANANYSIS

Observed Variables:

LS1 LS2 LS3 LS4 S5 LS6 LS7 LS8 DEP1 DEP2 ANX1 ANX2

correlation matrix from file LS.pom

asymptotic covariance matrix from file LS.acc

sample size:452

latent variables:Lstyle DEP ANX

relationshios:

LS1=1#LStyle

LS2－LS8=LStyle

DEP1=1#DEP

DEP2=DEP

ANX1=1#ANX

ANX2=ANX

DEP=LStyle

ANX=LStyle

lisrel output:nd=3 sc me=wls

path diagram

end of problem

根据 Jöreskog ＆ Sörbom〔9〕的建议，本研究报告了一些主要的拟合指数，具体指标见表2。各项拟合指数均达到理想水平，假设模型得到验证。

生活方式与抑郁和焦虑之间关系的完全标准化解见图1，图中各个参数的t检验均达到0.01的显著水平。生活方式量表中的八个项目一致地聚合为一个潜在变量，即生活方式;并且与抑郁和焦虑呈负相关关系。也就是说，生活方式越健康，患抑郁症和焦虑症的几率就越低;生活方式越不健康，抑郁和焦虑的程度就越高。

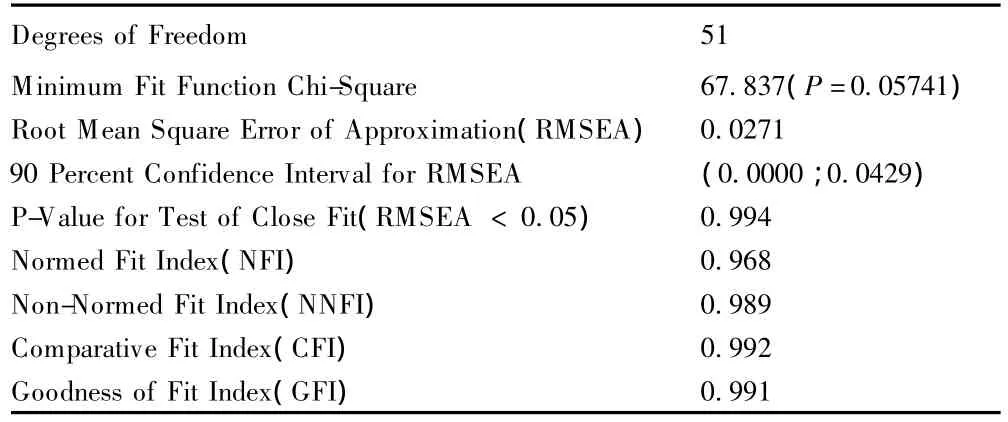
表2 假设模型的主要拟合指标(N=452)

图1 生活方式与抑郁和焦虑之间关系的路径图

讨 论

类别变量的结构方程模型处理的是可以转化为梯阶型的观测变量，类别变量的分类间距既可以相等，也可以不等，至于作为分类基准的潜在连续型变量的意义是什么并不重要，它仅仅是一个工具性假设而已。类别变量的结构方程模型尤其适用于类似李克特量表(Likert scale)等方面的研究，由于需要使用不同的分析技术，应用上受到了一定的限制，但随着统计软件的不断开发，类别变量的结构方程模型的应用也将越来越广泛，越来越准确。除了LISREL以外，其他包含结构方程模型的软件也提供了类别变量的结构方程模型分析工具，比如、MPLUS、EQS等等。

在同时涉及不同类型变量的情况下，相关系数变得更加复杂，连续变量间需要估计的是皮尔逊相关系数，类别变量间需要估计的是多项相关系数，类别变量与连续变量间需要估计的是多列相关系数(polyserial correlations)。LISREL软件中的“PRELIS”可以实现三种不同相关系数的估计，只要在“Data－Define Variables”指令下对变量的类型进行定义就可以了，相关的分析与类别变量结构方程模型的分析方法完全相同。

结构方程模型是一种有效的研究方法和统计技术，在公共卫生领域也有广泛的应用〔10－12，14〕。如果使用不恰当，就会导致不正确的统计推断。观测变量的类型是需要考虑的重要因素之一，它直接影响到分析矩阵的构成和参数的估计方法。

(致谢 本论文的完成得到暨南大学211项目资助以及暨南大学“国家大学生创新性实验计划”资助，在此一并表示感谢。)

1.Do Toit S，Do Toit M，Mels G，et al.LISREL for Windows:PRELIS User's Guide.2008，Lincolnwood，IL:Scientific Software International，Inc

2.Browne MW.Asymptotically distribution－free method for the analysis of covariance structure.British Journal of Mathematical and Statistical Psychology，1984(37):62－83.

3.Lowe B，Wahl I，Rose M，et al.A 4－item measure of depression and anxiety:validation and standardization of the Patient Health Questionnaire－4(PHQ－4)in the general population.Journal of Affect Disorders，2010(122):86－95.

4.Jensen LW，Decker L，Andersen MM.Depression and health－promoting lifestyles of persons with mental illnesses.Issues in Mental Health Nursing，2006(6):617－634.

5.Tanaka H，Sasazawa Y，Suzuki S，et al.Health status and lifestyle factors as predictors of depression in middle－aged and elderly Japanese adults:a seven－year follow－up of the Komo－Ise cohort study.BMC Psychiatry，2011(7):11－20.

6.Belloc NB，Breslow L.Relationship of physical health status and health practices.Preventive Medicine，1972(1):409－421.

7.Morimoto K.Lifestyle and health.Japanese Journal of Hygiene，2000(54):572－591.

8.Toda M，Makino H，Kobayashi H，et al.Health－related lifestyle and travel patterns of behavior related to health effects of leisure.Social Behavior and Personality，2007，35(3):287－294.

9.Jöreskog KG，Sörbom D.LISREL 8:Structural equation modeling with the SIMPLIS command language.Mooresville，IN:Scientific Software，Inc.1993.

10.张宜民，冯学山.公立医疗机构医生工作满意度结构的验证性因素分析.中国卫生统计，2011，28(1):29－32.

11.张鹏，楼超华，Laurie，等.上海未婚青少年性相关行为影响因素结构方程模型分析.中国卫生统计，2011，28(2):139－141.

12.何勃夫，孙涛，柳晓琳，等.基于结构方程模型的工作生活质量与离职倾向关系的整合模型构建.中国卫生统计，2011，28(2):168－170.

13.李鹏，蔡丽，崔壮.天津市某三甲医院阑尾炎患者住院费用影因素的结构方程模型分析.中国卫生统计，2011，28(2):161－164.