一些卡方积图的符号星控制数

丁宗鹏，徐保根，张亚琼

(华东交通大学基础科学学院，江西 南昌，330013)

1 引言及定义

本次研究所考察的图均为无向简单图，文中未说明的符号和术语均与文献［1］相同。

近几年来，图的控制理论的研究内容越来越丰富。加拿大著名图论专家COCKAYNE E J等先后引入了图的许多不同类型的控制概念及其变化形式后，图的控制理论出现了大量的研究成果。然而绝大多数是属于图的点控制，边控制的研究成果还相对较少。在文献［7］中徐保根定义了图的符号边控制概念，并获得了较多的研究成果，随后又从图的符号边控制拓展到了符号星控制上，并得出了一系列的研究成果。笔者在已有成果的基础上又确定了几类特殊图的符号星控制数。

设一个图G=(V，E)，v∈V，则v点在G中的边邻域定义为E(v)={uv∈E∣u∈V}。

定义 设G=(V，E)是一个没有孤立顶点的图，如果一个函数f:E→{+1，－1}，对一切v∈V(G)满足)≥1成立，则称f为图G的一个符号星控制函数。图G的符号星控制数定义为γ'ss(G)=minf为G的符号星控制函数}。

为了方便，如果f为G的一个符号星控制函数，则称满足f(e)=1的边e是在f下的1边;同样称满足f(e)=－1的边e是在f下的－1边。

2 主要结果及其证明

定理1 对于图G=Pm×Pn，当m，n为奇数且均大于1时，γ'ss(Pm×Pn)=mn－m－n+7。当m，n不全为奇数且均大于1时，γ'ss(Pm×Pn)=mn－m－n+4。

证明 情形1 当m，n全为奇数且均大于1时，对于图G中其度数d(v)=2的点所关联的边均标号1。对于图G中其度数d(v)=3或4的点(共(mn－4)个)，依据符号星控制的定义，每个点至多邻接1条－1边，从而图G中至多有(－1)条－1边(如果图G中至少有即为条边标号－1，那么至少存在一个点邻接了2条－1边，这不满足符号星控制的定义，矛盾)。从而有

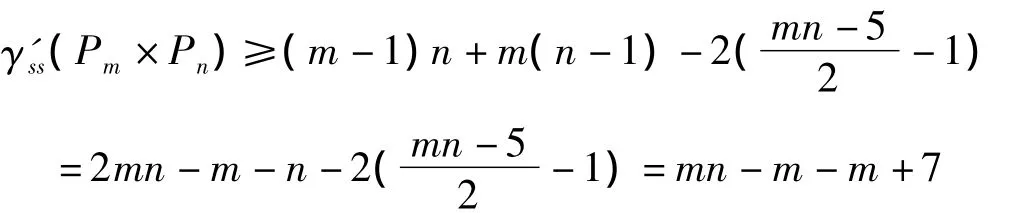
另一方面，给出图G的一个标号，步骤如下:

将图G=Pm×Pn画在平面上，使其成m行n列的格图。

(1)对图G中其度数d(v)=2的点所关联的边均标号1(共8条)。

(2)对第一行和最后一行余下的所有行边以－1，1依次交错标号。

(3)对第二行到倒数第二行的所有奇数行边标号－1。

(4)对最后一列余下的所有列边以－1，1依次交错标号。

(5)对图G剩下的所有边均标号1。

不难验证此标号符合符号星控制的定义。于是有

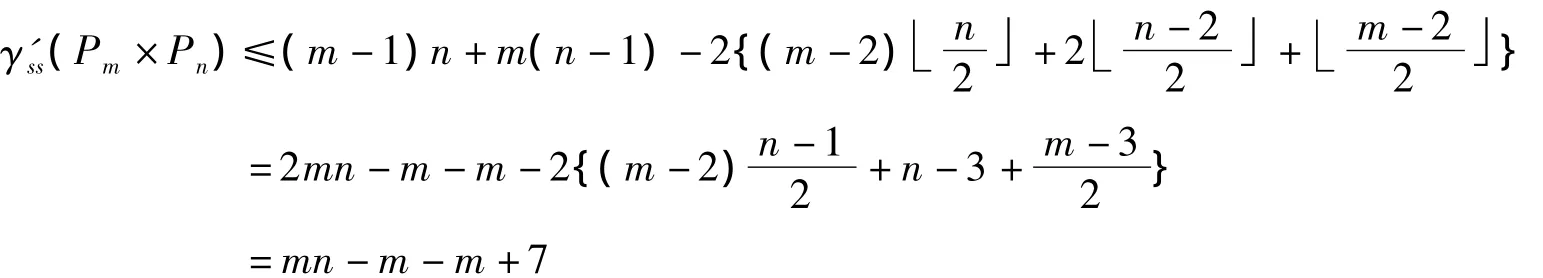
综上，当m，n全为奇数时，γ'ss(Pm×Pn)=mn－m－n+7。

情形2 当m，n不全为奇数均大于1时，不妨设n为偶数。对于图G中其度数d(v)=2的点所关联的边均标号1，对于图G中其度数d(v)=3或4的点(共(mn－4)个)，依据符号星控制的定义，每个点至多邻接1条－1边，从而图G中至多有(mn－4)/2条－1边。

从而有γ'ss(Pm×Pn)≥(m－1)n+m(n－1)－2·(mn－4)/2=mn－m－n+4。

另一方面，给出图G的一个标号，步骤如下:

将图G=Pm×Pn画在平面上，使其成m行n列的格图。

(1)对图G中其度数d(v)=2的点所关联的边均标号1(共8条)。

(2)对第一行和最后一行余下的所有行边以－1，1依次交错标号。

(3)对第二行到倒数第二行的所有奇数行边标号－1。

(4)对图G剩下的所有边均标号1。

不难验证此标号符合符号星控制的定义。于是有

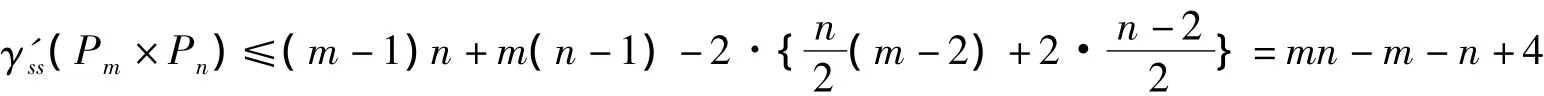
综上，当m，n不全为奇数时，γ'ss(Pm×Pn)=mn－m－n+4。证毕。

定理2 对于图G=Pm×Cn，当n为偶数时，γ'ss(Pm×Cn)=mn－n。

当n为奇数，m为偶数时，γ'ss(Pm×Cn)=mn－n。

当n为奇数，m为奇数时，γ'ss(Pm×Cn)=mn－n+1。

证明 情形1 当n为偶数时，对于图G中其度数d(v)=3或4的点(共mn个)，依据符号星控制的定义，每个点至多邻接1条－1边，从而图G中至多有(mn/2)条－1边。

从而有 γ'ss(Pm×Cn)≥(m－1)n+mn－2·mn/2=mn－n。

另一方面，给出图G的一个标号，步骤如下:

将图G=Pm×Cn画在平面上，使其成m个圈n条柱的图。

(1)对图G中的m个圈，对应取出每个圈上的最大独立边集(条)标号－1。

(2)对图G中剩下的所有边均标号1。

不难验证此标号符合符号星控制的定义。于是有

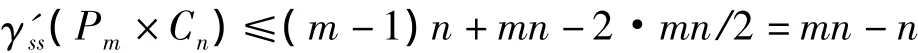
综上，当n为偶数时，γ'ss(Pm×Cn)=mn－n。

情形2 当n为奇数，m为偶数时，对于图G中其度数d(v)=3或4的点(共mn个)，依据符号星控制的定义，每个点至多邻接1条－1边，从而图G中至多有(mn/2)条－1边。

从而有 γ'ss(Pm×Cn)≥(m－1)n+mn－2·mn/2=mn－n。

另一方面，给出图G的一个标号，步骤如下:

将图G=Pm×Cn画在平面上，使其成m个圈n条柱的图。

(1)对图G中的m个圈，对应取出每个圈上的最大独立边集(条)标号－1。

(2)在所有邻边均未标号的一条柱上，取出其最大独立边集(条)标号－1。

(3)对图G中剩下的所有边均标号1。

不难验证此标号符合符号星控制的定义。于是有

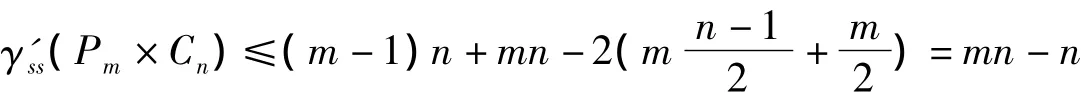
综上，当n为奇数，m为偶数时，γ'ss(Pm×Cn)=mn－n。

情形3 当n为奇数，m为奇数时，对于图G中其度数d(v)=3或4的点(共mn个)，依据符号星控制的定义，每个点至多邻接1条－1边，从而图G中至多有「」条－1边。

另一方面，给出图G的一个标号，步骤如下:

将图G=Pm×Cn画在平面上，使其成m个圈n条柱的图。

(1)对图G中的m个圈，对应取出每个圈上的最大独立边集(条)标号－1。

(3)对图G中剩下的所有边均标号1。

不难验证此标号符合符号星控制的定义。于是有

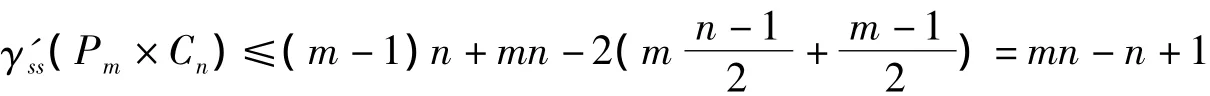
综上，当n为奇数，m为奇数时，γ'ss(Pm×Cn)=mn－n+1。证毕。

［1］ 徐保根.图的控制理论［M］.北京:科学出版社，2008.

［2］ BONDY JA，MURTY V SR.Graph theory with applications［M］.New York:Elsevier，1976.

［3］ HAYNESTW，HEDETNIEMIST，SLATER P J.Domination in graphs［M］.New York:Marcel Dekker INC，1998.

［4］ F·哈拉里.图论［M］.上海:上海科学技术出版社，1980.

［5］ XU Bao－gen.On minus domination and signed domination in graphs［J］.Journal of Mathematical Research ＆ Exposition，2003，23(4):585－590.

［6］ 徐保根.两类图的符号星控制数［J］.华东交通大学学报，2005，22(4):146－148.

［7］ XU Bao－gen.On signed edge domination of graphs［J］.Journal of Mathematical Research and Exposition，2007，27(1):7－12.

［8］ 徐保根，李春华.图的符号星k控制数［J］.纯粹数学与应用数学，2009，25(4):638－641.

［9］ XU Bao－gen.On signed cycle domination in graphs［J］.Discrete Math，2009(4):309:1 007－1 012.

［10］ 黄中升，邢化明，赵燕冰.图的逆符号边控制数的上界［J］.应用数学学报，2010，33(5):840－846.