船体型线多学科设计优化系统重构研究＊

李 翼 冯佰威

（福建船政交通职业学院1） 福州 350007） （武汉理工大学交通学院2） 武汉 430063）

从优化设计角度来看，船舶水动力性能的综合优化是一个多学科设计优化问题．例如，意大利罗马水池D．Peri教授利用多学科设计优化方法，完成了阻力、耐波两学科三目标的优化问题［1－4］；日本京都大学的Tahara．Y教授利用自开发集成框架，完成了阻力和推进的多学科多目标优化［5］；德国S．Harries教授基于船型特征的分析，开发一套全参 数 化 的 商 业 CAD 软 件 Friendship［6－7］，利用modeFRONTIER集成优化平台对CAD软件（Friendship）和CFD数值求解软件进行了集成，完成了船舶水动力性能多学科多目标优化工作，并对优化结果进行了模型试验验证．本文从构建实用的船体型线多学科设计优化平台角度出发，重点阐述优化系统的重构方法．

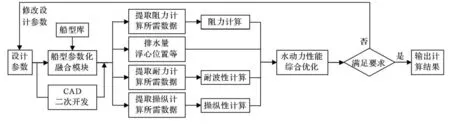
图1 基于CAD的船体型线多学科设计优化流程

1 船体型线的多学科设计优化流程

船体型线多学科设计优化流程如图1所示，简述如下：（1）设计参数即为控制船型变化的优化变量；（2）船型参数化融合模块读入设计参数，通过母型船的融合，生成新的船型［8］；（3）自动提取阻力计算、耐波性能计算及操纵性能计算所需要的数据文件，同时计算排水量及浮心的纵向位置；（4）阻力计算软件、耐波性能计算软件及操纵性能计算分别读取相应数据文件，并计算相关性能指标；（5）选择合适的优化算法，进行船型水动力性能综合优化；（6）自动评判获得的船体形状是否为水动力性能最优的船型，如果不满足要求，则再自动更改设计参数，重复上述步骤的（2）～（5），直至找到水动力性能综合兼优的船型．上述整个流程可借助多学科设计优化集成软件来实现．

2 系统重构的方法

目前国际上应用较为普遍的优化系统重构方法主要有：多学科可行方法（multidisciplinary feasible，MDF）、单学科可行方法（individual discipline feasible，IDF）、协同优化算法（collaborative optimization，CO）、并行子空间优化方法（concurrent subspace optimization，CSSO）［9］．

2.1 基于MDF方法的船型优化系统重构

MDF方法是解决MDO问题的最常用的方法，也称为All－in－One方法．在这种方法中，需要提供设计变量XD，通过执行一个完全的多学科分析（MDA）确保多学科的一致性，利用XD获得系统经过MDA分析后的输出变量U（XD），然后利用XD和U（XD）对目标函数F（XD，U（XD））和约束函数g（XD，U（XD））进行评估．MDF优化模型表述如下．

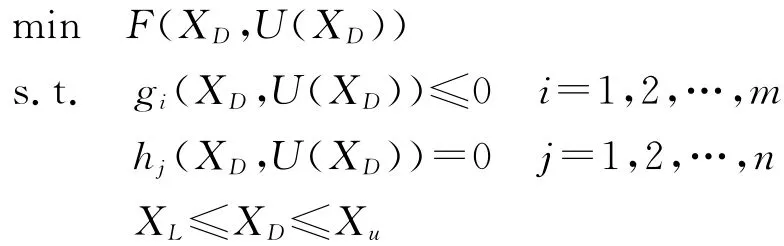
图2显示了MDF方法优化过程中的数据流．式中：mij为样条系数，通过对学科j的输出进行Fij处理后获得的；Fij为插补或者逼近系数；映射Eij为对样条的评估，代表从学科j到学科i的映射．

图2 MDF模型

根据图2的MDF模型，建立基于MDF方法船型优化系统结构，见图3．由图3可以看到该方法的系统结构包括一个优化器和一个多学科分析过程，船舶的阻力分析、耐波性分析、操纵性分析是按照一种串行的顺序依次执行，系统层的设计变量均为各子学科的设计变量，如船长（L）、船宽（B）、型深（D）、船型融合系数（Ci）等．所有学科的分析指标都作为系统的优化目标．采用MDF方法的这种系统结构，完成一次迭代计算需要分别执行船型融合、阻力分析、操纵性分析、耐波性分析，这种串行的方式必然要花费大量时间，难以进行有效的优化设计．

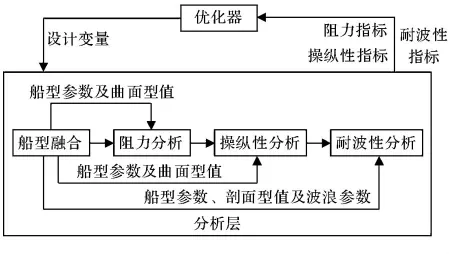
图3 基于MDF方法的优化系统结构

2.2 基于IDF方法的船型优化系统结构

单学科可行方法是E．J．Cramer等人提出来的，它提供了一种在优化时避免完全MDA分析的途径．IDF保留了单学科的可行性，同时通过控制学科之间一致性约束，驱动单学科向多学科的可行性和最优性逼近，也就是通过耦合变量将各单个学科的分析与系统整体优化连接起来．在IDF中，代表在学科间通信或耦合的参数被作为优化变量对待，事实上它们就是单个学科分析解决问题时的设计变量．IDF优化模型表述如下．

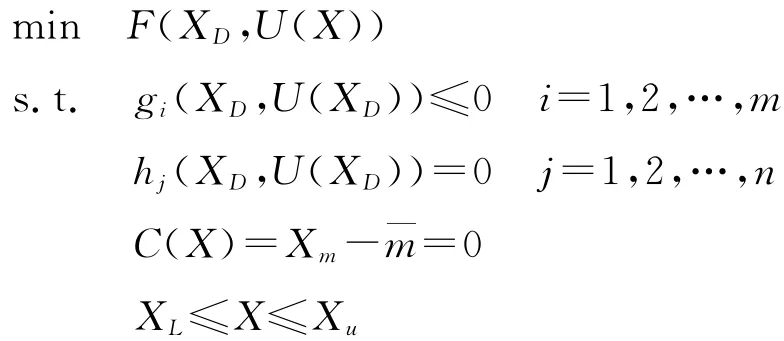
式中：XD为设计变量；Xm为学科间耦合变量；C（X）为学科间一致性约束．在实际应用中，通常令Jj＝C2j≤0．000 1，j＝1，2，…，学科数．图4为IDF方法的模型图．

图4 IDF模型

分析整个优化系统的结构，各性能学科之间的耦合主要体现在系统设计变量之间的紧耦合，利用IDF方法将图所示的优化系统进行重构．具体过程为：将优化系统分解为系统层及子系统层，由于船型融合程序为各性能分析程序提供统一的计算模型，因此，将船型融合程序规划在系统层调用，各性能分析程序规划在子系统层调用．系统层传递船型参数、曲面型值等到子系统层，而子系统层计算的性能指标再反馈到系统层．重新规划后的船型优化系统结构，见图5．

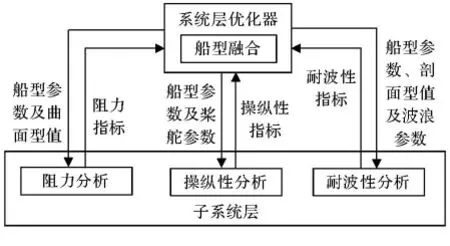
图5 IDF方法的优化系统结构

按照图5所示的IDF优化系统结构，在iSIGHT集成框架上重新规划优化问题，如图6所示．

图6 设计分析程序的过程集成

3 优化实例

以46 000t油船主尺度及型线的优化设计为例，在优化过程中重点考虑了主尺度及型线的变化对水动力性能影响，经济性暂未考虑．

1）优化的数学模型 优化变量：船长（L）、船宽（B）、型深（D）、吃水（T）、船型融合系数（Ci）；目标函数，min maxHeave（垂荡峰值最小），min maxPitch（纵摇峰值最小），min Rave（单位排水量总阻力最小），max K／T（诺宾指数最大）．

2）约束条件 （1）GM／B≥0．03，GM 为初稳性高度；（2）浮力平衡，Displacement＝DWT＋LWT．Displacement为排水量，LWT 为空船重量，DWT 为载重量；（3）舱容约束，CV／CV0≥1．

……

3）指标计算 （1）耐波计算，由自编切片程序计算垂荡及纵摇的幅值；（2）操纵性计算，由自编程序计算诺宾指数；（3）阻力计算，采用商业软件Shipflow计算兴波阻力，粘性阻力采用Holtrop方法估算．

4）优化算法 选择多目标遗传算法（NSGA），种群数设置为50，遗传代数设置为50．

为使两种系统重构方法具有可比性，作者分别采用MDF方法及IDF方法对本例进行了优化．由于本例的优化属于多目标优化问题，因此优化后将获得一系列的非劣解，也即Pareto解集，如图7、图8所示．从Pareto解集中可选择各性能指标均明显改善的解，见表1及表2．

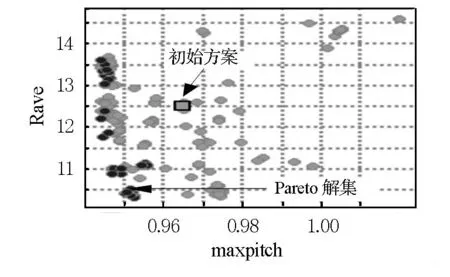
图7 基于MDF方法获得Pareto解集

图8 基于IDF方法获得的Pareto解集

表1 基于MDF方法的船型优化结果

表2 基于IDF方法的船型优化结果

4 结 论

1）采用不同的系统重构方法进行船型水动力性能综合优化，均能有效提高船型的设计质量．由表1和表2可知，各水动力性能指标均比母型有了明显的提高．但值得说明的是，尽管两类优化的初始条件相同，但最终获得的优化结果却有差别，这与遗传算法属于概率性搜索算法有关．

2）对比两类不同的优化结果可知，基于MDF方法的船型优化需要更长的优化时间，这与各性能计算程序串行执行有关．而基于IDF方法的船型优化采用的是并行计算的系统架构，故其需要的优化时间会更短．

3）综合以上2点，对船型水动力性能综合优化而言，采用IDF方法对优化系统进行重构无疑是一种理想的方法．本文的研究为船型水动力性能多学科设计优化平台走向实用化打下了基础．

［1］PERI D，ROSSETTI M，CAMPANA E F．Design optimization of ship hulls via CFD techniques［J］．Journal of Ship Research，2001，45（2）：141－149．

［2］PERI D，CAMPANA E F．Multidisciplinary design optimzation of a naval combatant［J］．Journal of Ship Research，2003，47（1）：1－12．

［3］PERI D，CAMPANA E F．High－fidelity models and multiobjective global optimization algorithms in simulation－based design［J］．Journal of Ship Research，2005，49（3）：159－175．

［4］PERI D，CAMPANA E F，DATTOLA R．Multidisciplinary design optimization of a naval frigate［C］／／10th AIAA／ISSMO Symposium on Multidisciplinary Analysis and Optimization，Albany，NY，2004．

［5］TAHARA Y，TOHYAMA S．CFD－based multi－objective optimization method for ship design［J］．International Journal For Numerical Methods In Fluids Int．J．Numer．Meth．Fluids，2006，52：499－527．

［6］HARRIES S，ABT C．Formal hydrodynamic optimization of a fast monohull on the basis of parametric hull design［C］／／5th International Conference on Fast Sea Transportation，Seattle，WA，1999．

［7］HARRIES S，VALDENAZZI F，ABT C，et al．Investigation on optimization strategies for the hydrodynamic design of fast ferries［C］／／6th International Conference on Fast Sea Transportation，Southhampton，UK，2001．

［8］冯佰威，刘祖源．多学科设计优化技术在船舶设计中的应用［J］．中国造船，2009，50（4）：109－116．

［9］王振国，陈小前．飞行器多学科设计优化理论与应用研究［M］．北京：国防工业出版社，2006．