基于最大信噪比算法在缸盖振动信号中的分离研究＊

（武汉理工大学能源与动力工程学院 武汉 430063）

0 引 言

柴油机缸盖振动信号富含柴油机运行时的状态信息，通过对其研究可以及时发现燃烧异常﹑气门间隙异常等故障，所以一直都是学者研究的热点．工作中，缸盖系统承受缸内气体压力、进气门关闭时的瞬态冲击、排气门关闭时的瞬态冲击及排气门开启时的压力波动等激励源的激励，这些激励都是随时间有规律的作用在缸盖上．为了便于分析，一般假设缸盖系统为稳定的线性系统，且各激励源彼此线性无关．由于这些激励在时域频域上均有所重叠，很难用传统的滤波方法从缸盖振动信号中分离出各主要激励源．盲分离技术兴起之后，有学者尝试将其应用在缸盖振动信号分离中，首先将柴油机工作时的主要激励源看作是未知源信号，在未知路径下混合成测得的缸盖振动信号，由缸盖振动信号反推未知源信号即为典型的盲分离数学模型．目前主要采取的是Fast－ICA算法［1］，该算法迭代步骤多﹑收敛速度慢﹑计算时间长，容易导致分离结果的失真．

为了能够效果更佳的分离主要激励源，研究新的盲源分离算法已势在必行．本文首先介绍了基于最大信噪比的盲源分离算法，该算法计算复杂度低﹑无须迭代，有很好的研究价值．而后将其运用在仿真的振动信号分离中，通过传输矩阵的比较说明其相对于传统盲源分离Fast－ICA算法的优势，而后在分析缸盖振动信号基本特征的基础上，实验测取4135柴油机第4缸的缸盖振动信号，利用基于最大信噪比的盲源分离算法对其分离，得到主要激励源的时频域图像，其与先验知识的吻合说明了该算法分离结果的准确性，这也为进一步判定柴油机内部零部件的状态以及其工作状态提供了理论依据．

1 最大信噪比盲源分离算法

设s为源信号，x为混合信号，y为恢复信号，W 为分离矩阵，误差e＝s－y为噪声信号．则信噪比函数为［2］

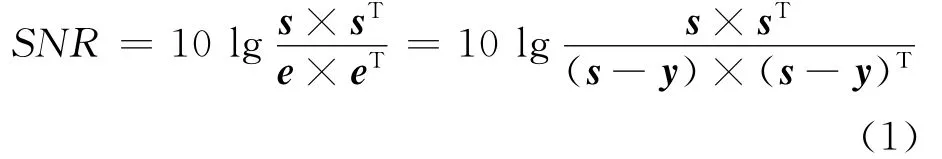
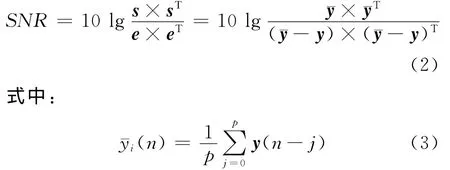
其中：p为滑动平均长度，一般取小于100的整数．

为了简化计算，式子中的y¯用y代替．得到最大信噪比的目标函数为

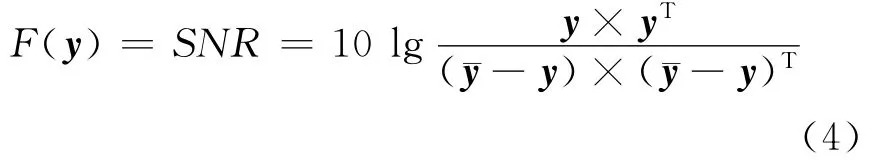
式中：y＝Wx；y＝Wx¯．x¯为混合信号x经滑动平均处理后的信号．

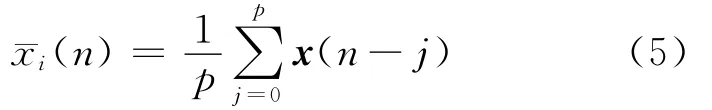
为了优化目标函数，方程（4）可以写成

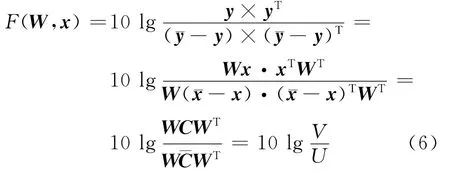
由式（6）可得关于分离矩阵W 的函数F的梯度为

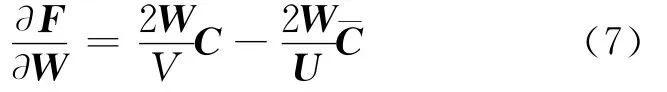
由于目标函数（4）的极值点为式（7）的零点，因此可以得到解方程为

可见，该算法的实质是将求优过程转为广义特征值问题求解，没有其他ICA算法冗长的迭代步骤，这也是该算法的优势所在．

2 算法在仿真振动信号分离中的应用

目前，针对最大信噪比盲源分离算法的研究还集中在语音信号分离中，已有试验表明该算法可以有效恢复语音源信号（超高斯分布），且在分离效果上较Fast－ICA算法更佳．以下进一步讨论基于最大信噪比算法在仿真振动信号分离中的适用性．

用以下3路信号模拟3路仿真振动信号，见图1．

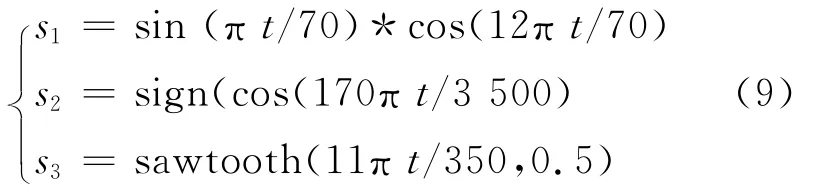
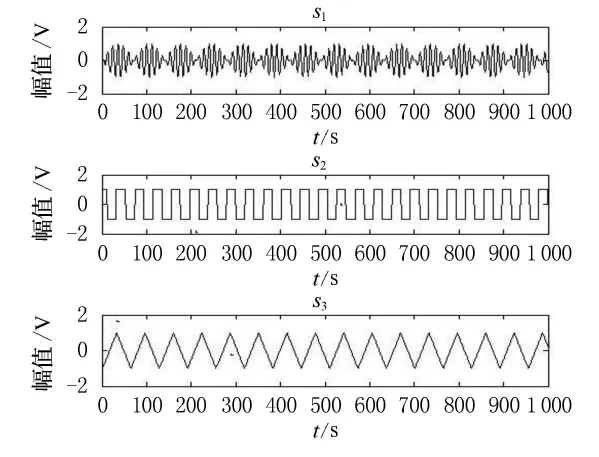
图1 仿真源信号

仿真振动信号经混合矩阵H得到混合信号为

用Matlab随机产生混合矩阵H

首先对混合信号作白化处理，而后使用本算法与基于负熵的Fast－ICA算法分离，分别得到传输矩阵B1和B2

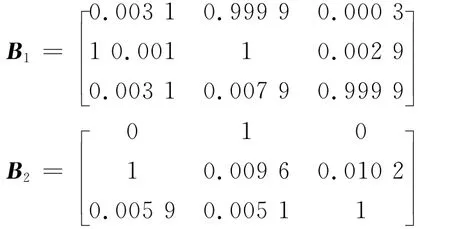
如图2，3所示，2种算法均可以较好的恢复仿真源信号．观察传输矩阵，传输矩阵B2中有2个元素均在0．01左右，超过0．005的总计有4个之多，而B1中只有1个（理想状况下这些元素应均为0），这定性说明最大信噪比算法对源信号分离效果更佳．下面进一步计算两种算法A矩阵的2范数来定量说明这个问题（其中H1，H2阵为代表理想分离结果的单位矩阵）．

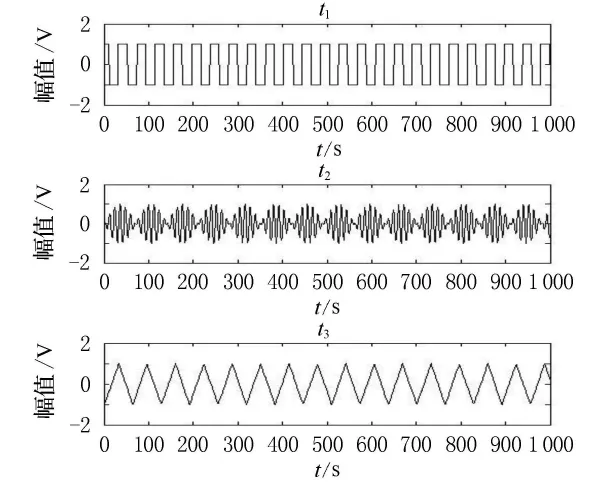
图2 最大信噪比算法盲源算法分离结果

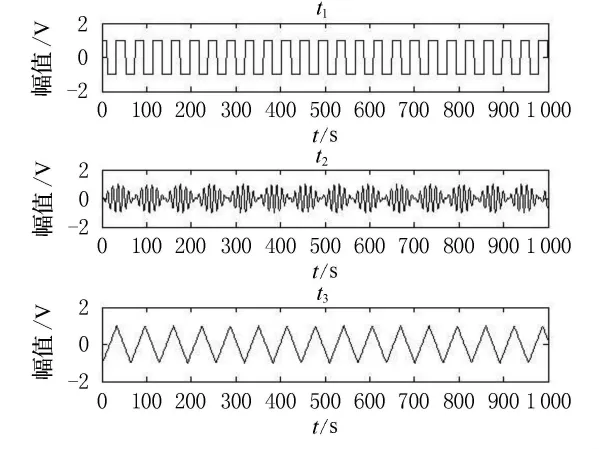
图3 基于负熵Fast－ICA算法分离结果

更清楚的说明全局最优算法分离效果较传统的基于负Fast－ICA算法更为良好．

3 算法在实测缸盖振动信号分离中的应用

3.1 缸盖振动信号分离模型

柴油机缸盖具有振源多、振动类型多样等特点，一般来说可将其看作是多输入、单输出的线性系统［3］．工作中内燃机缸盖主要承受进排气阀的开启和关闭等冲击力及缸内气体压力．系统输入是这些激励力，输出则是缸盖振动信号．激励力信号在时域内的波形，与喷油提前角和配气相位密切相关．当柴油机出现某种故障时，激励力源信号在作用时间和能量强度等方面将有改变，据此可进行故障诊断．

频域特性则是各激励力信号在频域内的特性，一般而言，进气门、排气门开启落座能量频段要比燃烧压力能量频段高．已有资料显示4135柴油机在运行状态下各激励段振动信号的功率谱，进气阀开启信号能量集中在大于6kHz以上的高频区域，气体压力产生的能量则集中在5kHz的中低频区域．6kHz为区分两者能量分布比较明显的边界频率．

3.2 实测缸盖振动信号的分离

实验对象为4135四冲程非增压柴油机，1，2缸共缸盖；3，4缸共缸盖，发火顺序为1－3－4－2．测点布置在第4缸缸盖上，测取5个通道的信号．其中1通道为上止点信号、2通道为气缸压力信号、3～5通道为缸盖振动信号．在转速1 200 r／min，75%负荷的工况下试验，通过对照可知采样点4 013点为第4缸发火上止点时刻．截取其前后25°，这段时间只有第3缸排气门开启时气体节流激励与第4缸的气体燃烧压力激励．由于采样频率为40kHz，对应采样信号点数范围为3 875点到4 151点．取3，4，5通道的信号进行分离．图4自上而下分别为上止点信号、气体压力信号和第4缸缸盖振动信号（第3通道）．

由于每个循环中特定曲轴转角范围内的一段振动信号，总是会与某个激励力相对应．截取特定时间段，主要考虑激励源数目较少模型容易简化．在分离模型中，将第4缸燃烧压力信号和第3缸的气阀开启信号看作源信号，其中混有高频噪音．通过传输路径混合后得到观测信号，即采集到的3路缸盖振动信号．

试验中为了让响应信号准确的反应气缸压力信号，将加速度传感器安装在气缸盖的正上方垂直拾取，这样减少其他因素干扰，比如活塞横向敲击缸套引起的振动．已有研究结果表明，缸盖表面正对各缸中心处的测点对气缸进排气门激励与气缸爆压激励响应最为敏感，所以选为振动测点．测点布置见图5．

图5 测点布置图

3路原始采样信号去均值并做平滑处理后，再经过设计的低通FIR滤波器，这里假设噪音为高于10kHz的高频噪音，滤波器截止频率设为10kHz，得到的3路振动信号，见图6．

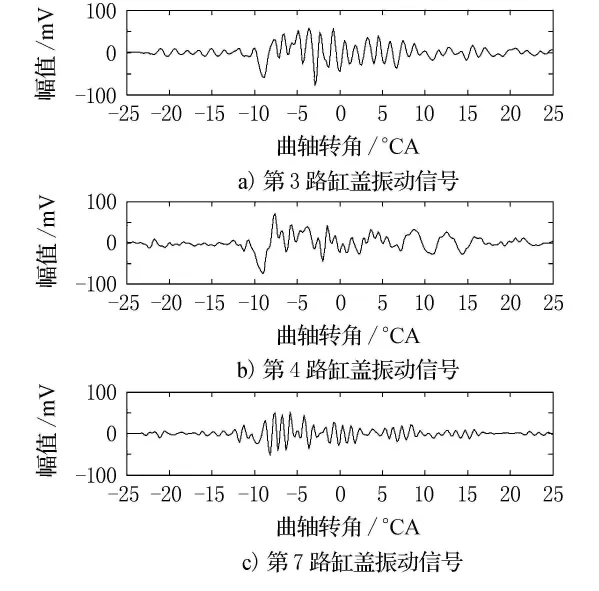
图6 处理后的3路缸盖振动信号

时域图上，振动信号均在第4缸发火上止点前10°左右开始发生明显的波动．这是由于第3缸排气门开启时气体节流作用及第4缸喷油提前导致缸内燃烧压力的剧烈波动所致．

使用Matlab软件编写该算法，采取主分量分析（PCA）［4］，只取分离矩阵较大2个特征值对应的特征向量．运算后得到两路激励源时域信号，见图7．这两路激励源信号的功率谱密度，见图8～9．

频域图上，频段能量分布与先验信息吻合，第3缸排气阀开启信号功率谱频段与第4缸燃烧压力信号功率谱频段在6kHz处有较明显的分界标志，侧面证明了该算法的有效性．

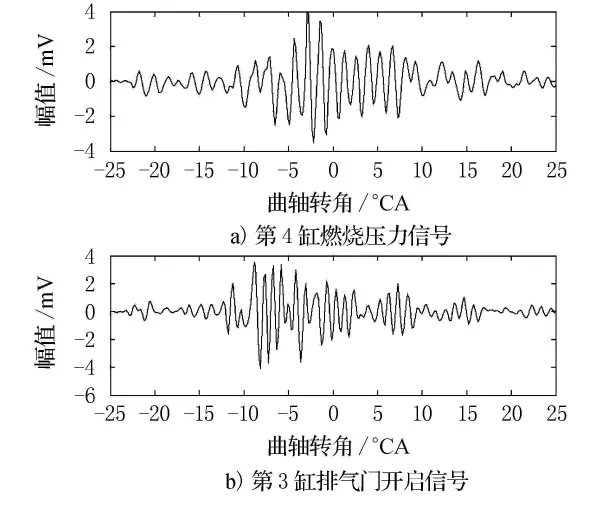
图7 处理后的3路缸盖振动信号

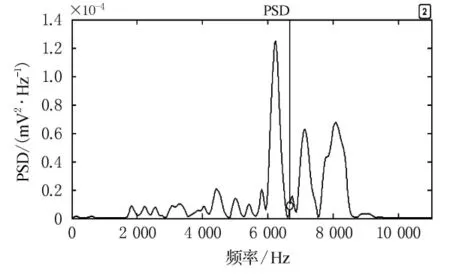
图8 第3缸排气门开启信号功率谱密度

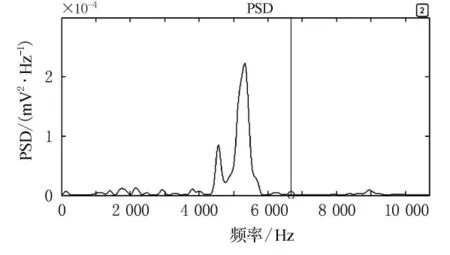
图9 第4缸燃烧压力信号功率谱密度

4 结 论

1）仿真振动信号分离试验结果表明：最大信噪比算法较传统的基于负熵的Fast－ICA算法效果更优．另外，该算法还有计算复杂度低、无须迭代等优点［5］．

2）针对目前缸盖振动信号难以分离出主要激励源的问题，本文将该算法应用在实测的柴油机缸盖振动信号中，证明了该算法可以有效分离出主要激励源，为后续的柴油机故障诊断提供理论基础．

［1］康 斌．独立分量分析在机械振动信号中的应用研究［D］．武汉：武汉理工大学，2008．

［2］马建仓，陈海洋．盲信号处理［M］．北京：国防工业出版社，2009．

［3］李 强，王太勇．故障源信号的频域盲分离及其应用研究［J］．机械强度，2009，15（2）：16－19．

［4］张发启，张 斌．盲信号处理及应用［M］．西安：电子科技大学出版社，2004．

［5］COMON P．Independent component analysis，a new concept［J］．Signal Processing，1994，36：267－270．