非独立情况下二维随机变量特征函数性质的推广与应用
吴雄韬,胡伯霞
(衡阳师范学院 数学与计算科学系,湖南 衡阳 421002)
0 引 言
特征函数是处理概率问题的有用工具,对随机变量序列的收敛问题起到很重要的作用,可以把随机变量序列的收敛问题转化为一般函数的序列的收敛问题来进行处理。独立情况下特征函数有很多的性质,如文献[1]-[2],特别是特征函数与随机变量的k阶矩之间的性质对于转化矩的计算有重要的现实意义,同时也有很多学者对独立情况下多维随机变量的特征函数的性质进行了研究如文献[3]-[5]而对于非独立情况,相应的结论几乎没有,本文在非独立情况下推广了特征函数的二阶导数与二阶矩及协方差之间的一些联系,并利用二维正态分布的特征函数对推广的性质进行了具体应用和检验。
设(X1,X2)是一个二维随机变量,为了讨论需要引入如下记号:
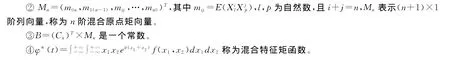
1 非独立情况下二维随机变量特征函数的性质
性质1.1 设(X1,X2)是一个二维随机变量,若X1+X2的特征函数φ(t)具有n阶连续导数,且X1与X2的n阶混合原点矩存在,则有φ(k)(0)=B×ik(k=1,2,…,n)。
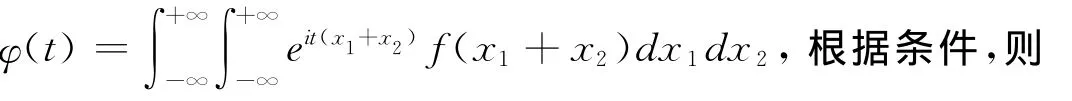

性质2 设φX1(t),φX2(t),φX1+X2(t)分别是X1,X2,X+X2的特征函数,且都二阶可导,φ*(x)为X1X2的特征函数,则有2φ*(t)=φ″X1(t)+φ″X2(t)-φ″X1+X2(t).
证明: 设(X1,X2)为二维连续型随机变量,其联合密度函数为f(x1,x2),离散情况可以类似处理,由于φX1(t),φX2(t),φX1+X2(t)二阶可导,则有

2 非独立情况下二维随机变量特征函数的性质


性质1.2正确性得到验证。
[1]孙荣恒.应用概率论[M].北京:科学出版社,2006.
[2]金冶明,李永乐.概率论与数理统计[M].长沙:国防科技大学出版社,1997.
[3]邱德华,文林.特征函数的性质[J].大学数学,2008,24(6):187-192.
[4]徐玉华.关于概率论中特征函数性质的几点讨论[J].荆州师范学院学报,2003,26(2):17-19.
[5]程伟.Banach空间中广义特征函数的性质及其应用[J].天津商学院学报,2006,26(6):48-50.
- 衡阳师范学院学报的其它文章
- Oscillation for the Solutions of Hyperbolic Partial Differential Equation with Damped Terms and High order Laplace Operator
- The Magnetic Behavior of Fe Doped Into Hexagonal Boron Nitride Sheet
- EmployingMixed Ligands to Construct 3d-4f Framework:Hydrothermal Synthesis,Structure and Magnetic Properties
- Application of Materialized View as Aggregate Table in Data Warehouse

