工字形截面叠合板式剪力墙损伤分析

徐 勤， 徐 林， 叶献国， 种 迅

（1.合肥工业大学 建 筑设计研究院，安徽 合 肥 230009；2.合肥工业大学 土 木与水利工程学院，安徽 合 肥 230009）

在结构抗震研究与设计中，需要选择一个合适的物理量描述结构在地震作用下的损伤程度。剪力墙是高层结构抗震的主要抗侧力构件之一，剪力墙的抗震性能决定了地震时的安全。为了有效控制地震作用下整体结构的损伤破坏，就要明确剪力墙构件各阶段的地震损伤程度［1］。

损伤指标是描述结构或构件受损伤程度的变量，一般定义为结构或构件受力损伤过程中某一累积量与相应的极限指标允许量之比。损伤指标值遵循单调递增的规律，即构件的损伤不可逆。本文采用应用较为广泛的基于刚度的Roufaiel损伤模型以及修正的Park－Ang损伤模型，计算了2个采用不同水平配箍率的工字形截面叠合板式剪力墙模型在循环荷载作用下的损伤，并将损伤模型计算结果与低周反复加载试验结果及现象进行对比。

1 试验概况

本试验设计了2个工字形截面叠合板式剪力墙试件SW1和SW2。叠合板式剪力墙由两侧预制墙板与核心现浇混凝土部分组成，如图1所示（图中斜线填充范围为预制混凝土部分）。墙板内还设置了由3根截面呈等腰三角形的上下弦钢筋以及弯折成型的斜向腹筋组成的格构钢筋，其作用主要是增强预制部分与现浇混凝土部分的连接和整体性，并保证预制构件在运输吊装过程中有足够的强度和刚度。2个试件的差别在于翼缘与腹板交接部位的配箍率不同，SW1配置的箍筋为B10＠100／A8＠150，SW2配置的箍筋为B12＠100／A8＠150，底部箍筋加密区高度均为800mm。2个试件的高度均为4m，试件尺寸及配筋见图1。

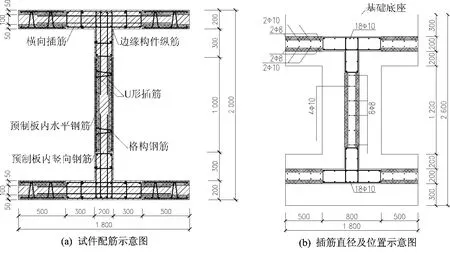
图1 试验试件尺寸及配筋示意图

本试验为拟静力试验，试验时在剪力墙的顶端施加水平低周反复荷载，加载装置如图2所示。试件屈服前采用力控制；试件屈服后改为位移控制，即按屈服时顶点位移δy的倍数逐级加载，每级循环3次，直至试件承载力下降到最大承载力的85%左右为止［2］。

图2 试验加载装置

2 试验结果分析

2.1 试验现象

试件的破坏等级一般可分为基本完好、轻微破坏、中等破坏、严重破坏、倒塌5个等级。当水平力较小时，试件均保持为弹性，未发现明显裂缝。随着荷载增加，首先在剪力墙与基础的连接处观察到明显的弯曲裂缝，荷载继续加大，墙板与基础连接处裂缝不断延伸和加宽，其他部位裂缝开展较少，宽度也较小。受力纵筋屈服之前，墙板与基础连接处裂缝宽度很小，卸载后也基本闭合，结构构件基本完好。当加载位移为2δy时，墙板与基础连接处最大裂缝宽度达到2.5mm左右，墙体其他部位也出现一定数量的弯曲裂缝和弯剪斜裂缝，但卸载后裂缝仍能基本闭合，残余宽度较小，试件属轻微破坏。当加载位移为4δy时，墙板与基础连接处最大裂缝宽度达到8mm左右，墙体裂缝也进一步增多，已有裂缝宽度加大，截面受压区混凝土保护层剥落，试件达到中等破坏。当加载位移为5δy时，墙板底部裂缝宽度开展更大，达到17mm左右，受拉侧墙体出现被拉起的现象，底部截面受压区混凝土开始逐渐被压碎，纵筋外露，试件严重破坏，不可修复。当加载位移为6δy时，截面受压区混凝土严重压碎，受拉主筋甚至出现被拉断现象，受压主筋压曲，试件破坏。

2.2 滞回曲线

试件的力－顶点位移滞回曲线如图3所示。试件从加载到破坏整个过程中表现出稳定的滞回特性。加载的初始阶段滞回环为梭形，随着剪力墙与基础间剪切滑移的逐渐增大，滞回环的反S形越来越明显，试件的滞回耗能较小。

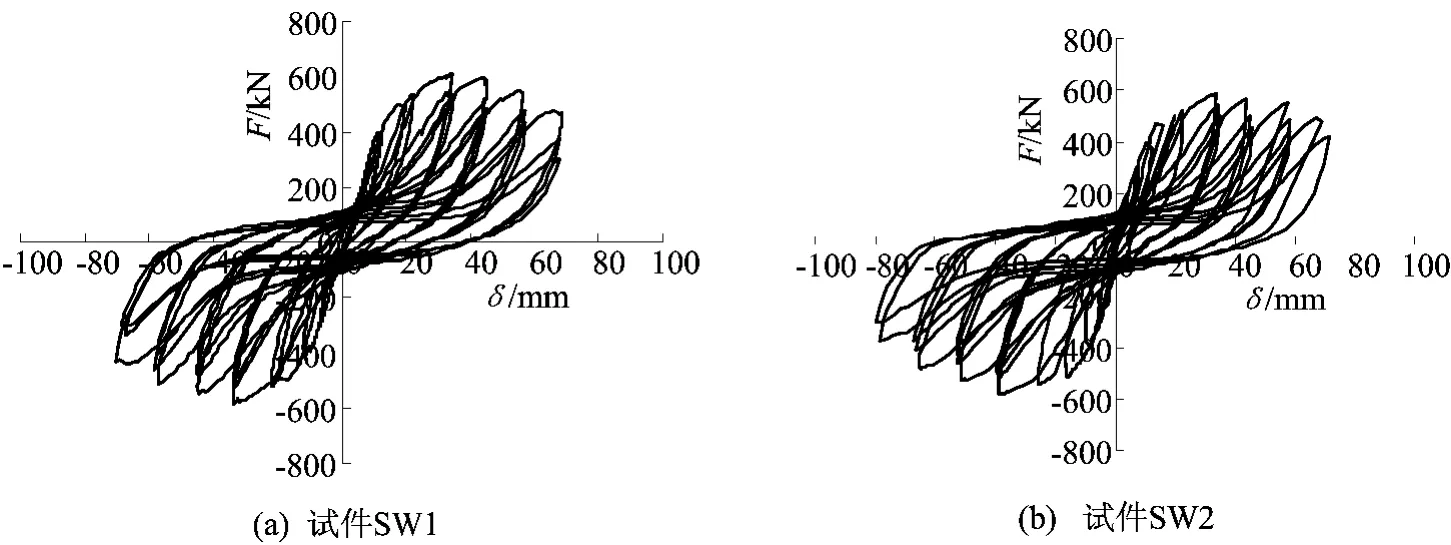
图3 试件力－顶点位移滞回曲线

2.3 骨架曲线特征点分析

骨架曲线各特征点［2］见表1所列。

表1中Fy为试件的屈服荷载，δy为试件的屈服位移，Ky为试件的屈服割线刚度，Ff为试件的极限荷载，δf为 试件的极限位 移，δf／δy为 试 件的延性系数。

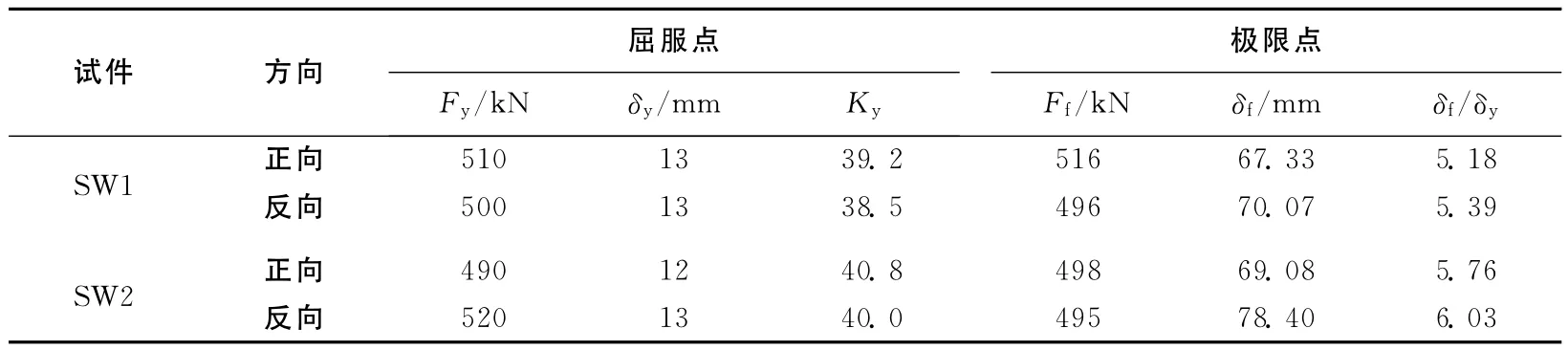
表1 各试件骨架曲线特征点

3 基于刚度的损伤分析

3.1 试件刚度实测值和衰减过程分析

结构的刚度能够反映其变形能力。随着荷载或位移的增加，构件的刚度会因其自身的累积损伤随着循环次数的增加而逐渐下降。为了定量地反映每次循环时试件刚度的退化程度，定义各级加载下的割线刚度Ki，其值可按（1）式计算：

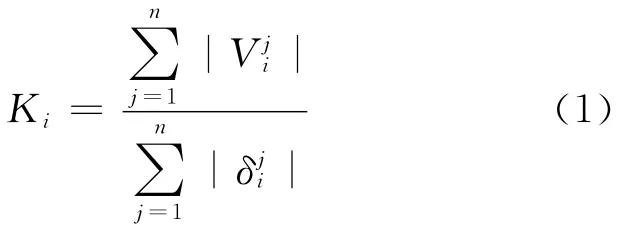
其中，Ki为第i级荷载作用下的刚度为第i级荷载第j次循环下的荷载为第i级荷载第j次循环下的位移。各试件的实测割线刚度退化曲线如图4所示。由图4可以看出，2个试件割线刚度的退化趋势大致相同：初始加载时，试件的割线刚度均较大；随着墙体底部与基础连接部位的开裂以及裂缝宽度的不断增大，割线刚度迅速退化；达到极限荷载后，墙体的主要裂缝已形成，割线刚度退化相对稳定，此时的刚度退化主要是次裂缝作用的结果；到试验后期，2个试件的残余割线刚度相差不大。

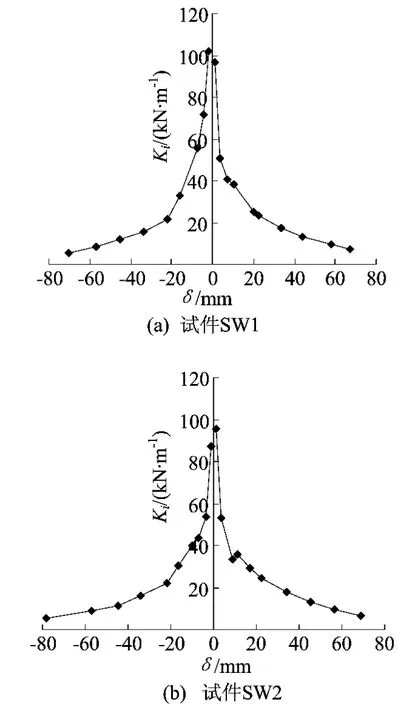
图4 试件割线刚度退化曲线

3.2 基于刚度的Roufaiel模型及结果分析

1987年Roufaiel和Meyer对Lybas和Sozen提出的基于刚度的损伤指标计算模型进行了修正，提出的损伤指标［3－4］为：

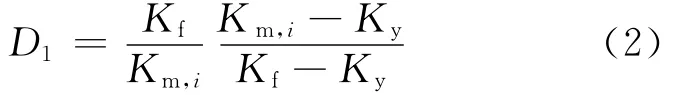
其中，Kf为构件的极限割线刚度；Km，i为构件在第i个循环时的割线刚度。

利用（2）式分别对2个试件在正向不同位移幅值时的损伤进行了计算。各试件的计算参数及结果见表2所列。由表2可以看出，采用Roufaiel模型得到的2个试件的损伤指标较为接近。

基于刚度的Roufaiel模型公式简单，使用方便，但它仅从刚度方面来考虑构件的损伤，对于地震作用下构件的累积滞回耗能产生的损伤考虑不够，难以真实反映构件的破坏机理，建议用于其他模型的辅助评估。

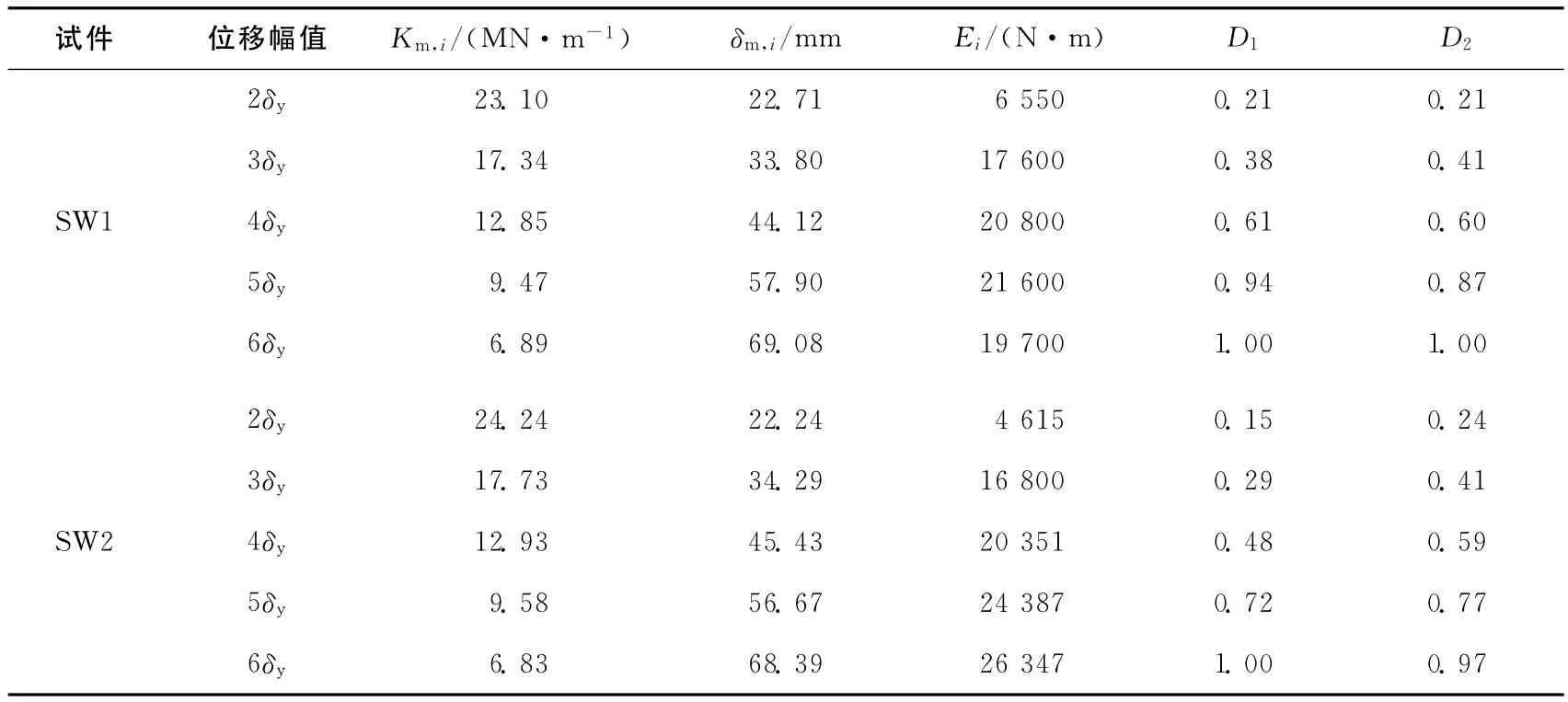
表2 损伤指标相关计算参数及计算结果

4 基于位移及耗能的损伤分析

4.1 试件耗能分析

结构耗能能力是评价结构抗震性能的一个重要指标，可用能量耗散系数E反映试件在不同阶段时的耗能能力，并作为试件的耗能指标。耗能系数计算示意图如图5所示。

图5 耗能系数计算示意图

计算公式为：

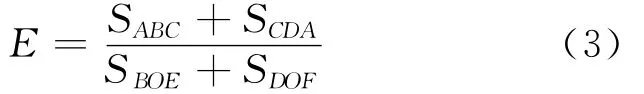
其中，SABC＋SCDA表示结构消耗的能量；SBOE＋SDOF表示在正反2个方向上，假定结构从加载直至极限位移时，一直处于弹性阶段下所吸收的地震能量。E值越大，则说明结构的耗能能力越大。

试件能量耗散系数与顶点位移相关曲线如图6所示。

图6 能量耗散系数与顶点位移相关曲线

由图6可见，2个试件的能量耗散系数在每个循环相差不大，试件SW1在达到峰值荷载后耗能系数略有下降，主要原因是在最后几个循环加载过程中，试件出现了严重的捏缩，这在试件的滞回曲线上也有所反映。

4.2 修正的Park－Ang模型及结果分析

目前地震工程界普遍认为结构在地震中破坏是由于变形和耗能的联合作用所造成的，1985年Park和Ang基于大量钢筋混凝土梁柱的试验结果，提出了综合考虑构件的变形和累积滞回耗能2个方面影响的地震损伤指标计算模型［5－6］，但Park－Ang模型的边界条件不够严谨，在构件的弹性阶段及完全破坏阶段，损伤指标的值超出0～1这一范围。针对这一缺陷，文献［7］提出了以下修正的Park－Ang模型：

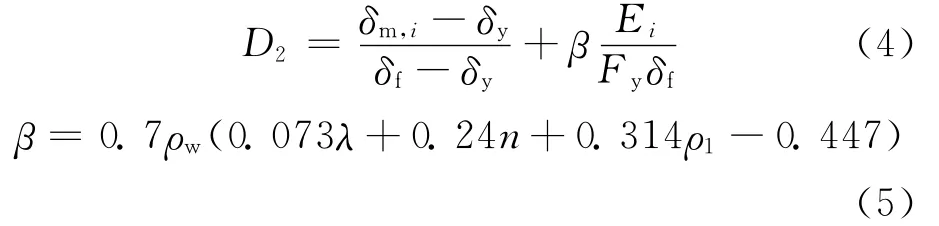
其中，δm，i为试件在第i个循环中的最大位移；δf为单调荷载作用下构件的极限变形；β为组合系数；Ei为第i个滞回环所包围的面积（即实际的累积滞回耗能）；λ为构件的剪跨比，当λ＜1.7时，取λ＝1.7；n为构件的轴压比，当n＜0.2时，取n＝0.2；ρw为构件的体积配箍率；ρ1为构件的纵向受力钢筋配筋率，当ρ1＜0.75%时，取ρ1＝0.75%。

2个试件的剪跨比为2.02，轴压比为0，纵向受力钢筋配筋率为0.53%，体积配箍率分别为1.57%和2.27%。利用修正的Park－Ang模型分别对2个试件在正向不同位移幅值时的损伤进行了计算，各试件的计算参数及结果见表2。文献［8］中提出的基于Park－Ang模型的损伤指标与结构损伤程度间的对应关系见表3所列。

表3 结构损伤程度与修正的Park－Ang损伤指标对照

由表3可见，D2基本符合表3中试件每一破坏阶段所对应的损伤指标取值范围。利用修正的Park－Ang模型计算结果与试验现象对比发现，该损伤模型能较好地反映试件在各阶段下的损伤情况。

5 结束语

通过对2个工字型叠合板式剪力墙试件的试验结果进行分析得出以下结论与建议：

（1）采用不同水平配箍率的叠合板式剪力墙试件，其刚度退化趋势大致相同，耗能能力未表现出明显的区别。

（2）本文计算的损伤模型均能在一定程度上反映2个工字型截面叠合板式剪力墙试件的损伤程度，也均能反映出水平配箍率的不同对构件损伤程度的影响。根据损伤模型计算结果和试验现象的对比分析可知，修正的Park－Ang模型与试验的实际情况吻合较好，能较好地评估试件的损伤程度。

（3）Roufaiel模型公式计算简单，使用较为方便，可用于其他模型的辅助评估。

［1］ 应 勇，蒋欢军，王 斌，等.钢筋混凝土剪力墙构件双参数地震损伤模型研究［J］.结构工程师，2010，26（5）：61－65.

［2］ 黄选明，曹万林，吕西林.不同型式暗支撑短肢剪力墙抗震性能试验研究［J］.地震工程与工程震动，2005，25（3）：60－66.

［3］ 连 星，叶献国，王德才，等.叠合板式剪力墙的抗震性能试验分析［J］.合肥工业大学学报：自然科学版，2009，32（8）：1219－1223.

［4］ Roufaiel M S L，Meyer C.Analytical modeling of hysteretic behaviour of R／C frames［J］.Journal of Structural Engineering，1987，113（3）：429－444.

［5］ Park Y J，Ang A H S.Mechanistic seismic damage model for reinforced concrete［J］.Journal of Structural Engineering，1985，111（4）：722－739.

［6］ Park Y J，Ang A H S，Wen Y K.Seismic damage analysis of reinforced concrete building［J］.Journal of Structural Engineering，1985，111（4）：740－757.

［7］ Kunnath S K，Reinhorn A M，Park Y J.Analytical modeling of inelastic seismic response of R－C structures［J］.Journal of Structural Engineering，1990，116（4）：996－1017.

［8］ 牛荻涛，任利杰.改进的钢筋混凝土结构双参数地震破坏模型［J］.地震工程与工程振动，1996，16（4）：44－54.