山岭隧道新奥法施工过程动态风险评估

刘 靖，艾智勇，苏 辉

（1.长安大学公路学院，陕西西安710064；2.河北省保定市交通局，河北保定071051；3.同济大学土木工程学院，上海200092）

随着国内经济建设尤其是交通网建设的快速发展，隧道工程也得到了越来越多的应用，并且规模也也来越大.但是，隧道工程作为地下工程的一部分，其地质状况的不确定性以及施工技术的复杂性决定了施工过程的巨大风险性，而安全事故的经常发生会对经济和社会造成很大的损失.因此，如何针对隧道工程的特点，建立及时、有效的风险评估体系，确保施工安全就成为亟待解决的现实问题.

目前，国内外一些学者对隧道工程中的风险问题进行了研究.Einstein等［1－2］较早地将风险理论应用于隧道工程，并针对隧道开挖的风险分析理念进行具体分析.Sturk等［3］在斯德哥尔摩环形公路隧道工程中应用了风险决策理论.此外，Kampmann等［4］、You等［5］也对隧道工程风险分析理论进行了深入研究.李永盛等［6］对崇明越江隧道工程进行风险评估，并提出了相应的风险规避措施.黄宏伟［7］、陈龙等［8］对于隧道和地下工程的风险分析进行了系统介绍.陈洁金等［9］则采用层次分析法（AHP）对隧道工程进行风险评估.

总的来说，目前对于隧道工程的风险分析还停留在静态分析阶段，对于施工过程的风险变化无法做出及时评估，因此难以确保整个施工过程中隧道开挖的稳定.鉴于此，本文将风险分析与新奥法施工量测体系相结合，对致险因子进行识别，确定风险评价指标体系，通过层次分析法确定各个量测项目的权重.引入模糊数学理论，建立合理的隶属度函数，对具体的量测数据进行模糊综合评判，结合权重分析和赋分体系即可得到综合风险指数，从而建立山岭隧道新奥法（NATM）施工过程动态风险评估模型.该模型可以将量测数据量化为单一的动态风险指数，并随着隧道开挖和量测的进行对施工风险进行动态评估.

1 新奥法施工动态风险评估模型

1.1 风险指标及评价体系

风险分析首先进行分析辨识，而风险辨识的目的则是找到相应的致险因子，风险辨识常用的方法有事故树法及WBS－RBS法等.从表1可看到，新奥法施工中的量测项目已对施工过程进行了较全面的监测.但是，单一的量测项目并不能完全反映施工风险情况.为此，将主要的量测项目作为风险评价指标，通过风险分析方法把各个量测项目数据量化为综合风险指数，从而省去了对众多量测数据分析的繁琐，并直观、有效地反映出隧道开挖的风险状态.

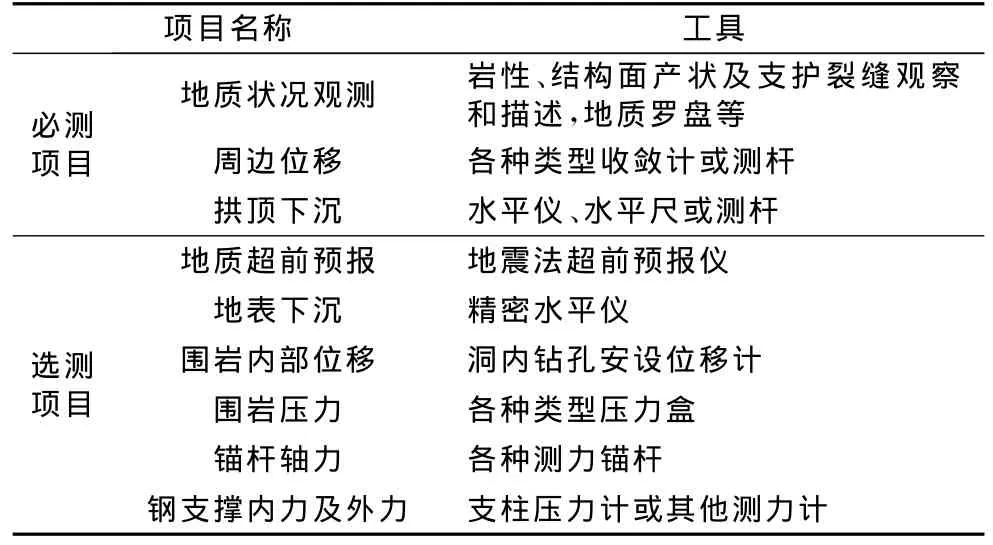
表1 新奥法施工常用量测项目Tab.1 Conventional measurement items of NATM construction

在分析多个隧道塌方案例的基础上，结合隧道工程新奥法施工量测特点，选择地质状况观测、周边收敛位移、拱顶沉降、地表沉降、锚杆轴力、锚杆抗拔力等六个量测项目作为我们动态风险分析的一级指标.对于每个量测项目，又进一步根据量测内容选取二级指标，整个动态分析指标体系如表2所示.

在确定风险指标之后，还需对各风险指标进行评价.为此，首先建立山岭隧道新奥法施工五级风险管理体制，如表3所示.对应各风险指标的风险等级，基于隧道量测规范和工程经验，建立各风险指标的评价体系，如表4所示.

表2 动态风险分析指标体系Tab.2 Index system of dynamic risk analysis

表3 风险等级Tab.3 Index of risk grades

为了便于评价，将表4中的周边收敛位移累计值、拱顶沉降累计值、地表沉降累计值及锚杆轴力评价指标做量纲一处理，即：A21／A，A31／A，A41／A，A为允许值；A51／D，A52／D，A53／D，D为设计轴力值.

1.2 指标权重确定

对于各指标权重确定，本文采用层次分析法［10］进行，这里仅以一级指标的权重计算为例进行说明.根据层次分析法中的1～9比例标度，可以编制出一级指标的层次分析评判矩阵，具体如表5所示.表5中，数字越大代表越相对重要，其具体取值是根据相关工程经验，由专家打分确定，带有一定的经验成分.

表5实际可构造为判断矩阵计算矩阵M的最大特征值λmax＝6，相应的归一化后的特征向量为

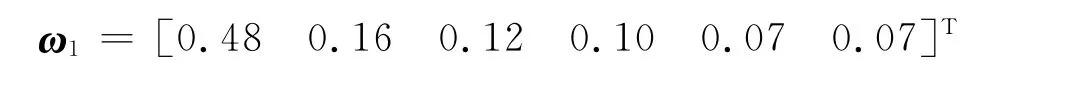
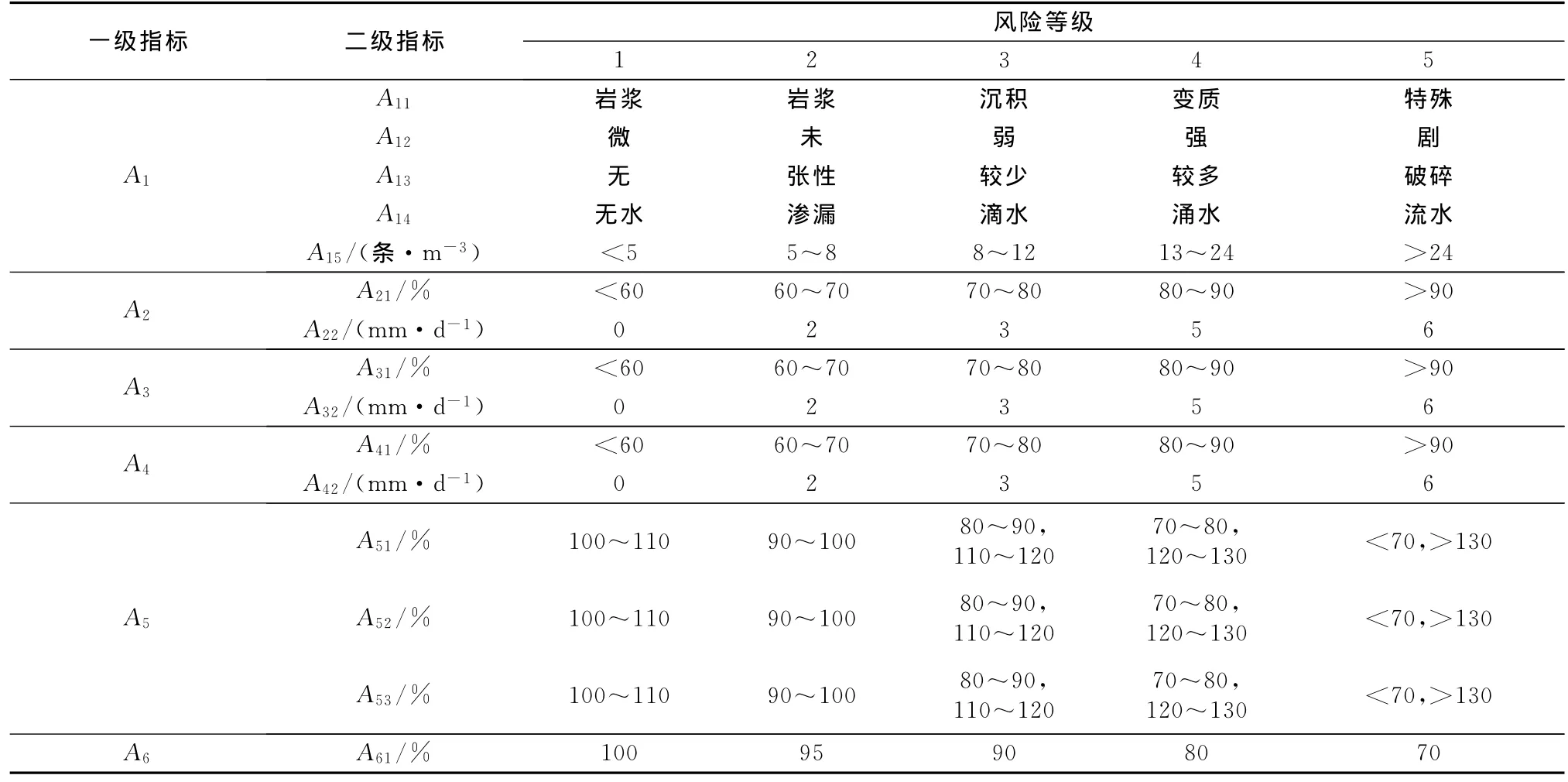
表4 风险指标评价体系Tab.4 Evaluation system of risk index

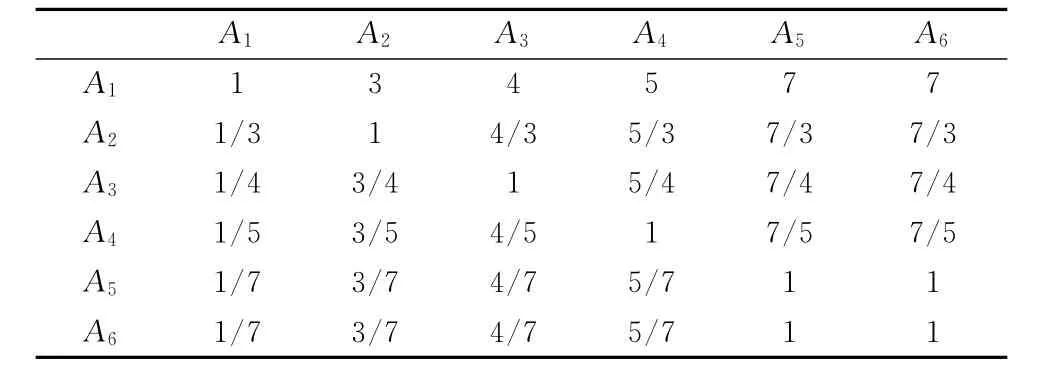
表5 一级指标层次分析取值表Tab.5 Value table of AHP for the first index

为刻画n阶对称矩阵M与一致性的接近程度，定义一致性指标（consensus index） C＝0，M有完全的一致性；C接近于0，M有满意的一致性.

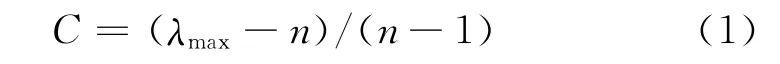
将上述矩阵M最大特征值λmax＝6代人式（1）可得到

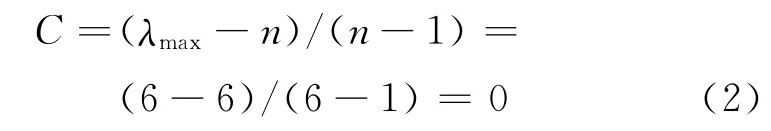
可见矩阵M具有完全的一致性.因此，我们可以得到六个一级指标地质状况观测、周边收敛位移、拱顶沉降、地表沉降、锚杆轴力、锚杆抗拔力的权重系数分别为0.48，0.16，0.12，0.10，0.07和0.07.同理，可以分别计算出各个二级指标的权重系数，计算结果如表6所示.

1.3 模糊综合评判

对于各实测数据的风险评价，引入模糊数学的模糊评判理念，即某一数据不是属于某一特定的风险等级，而是通过建立模糊评判矩阵对实测数据进行更准确的风险评价.

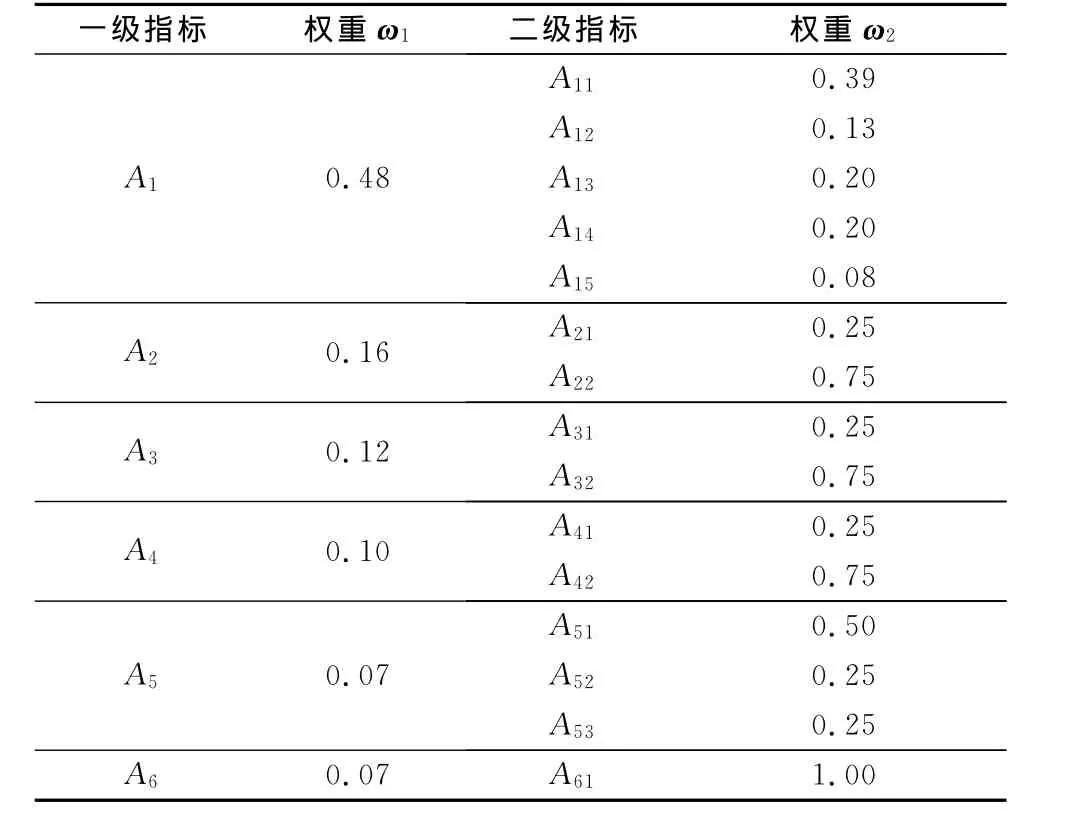
表6 风险指标权重表Tab.6 Weight coefficients for the risk index

模糊综合评判中最重要的是对于隶属度函数的选择，目前还没有成熟的确定方法，主要依靠经验以及通过实践反馈修正的方法进行.本文采取三角型隶属度函数分布，如图1所示.

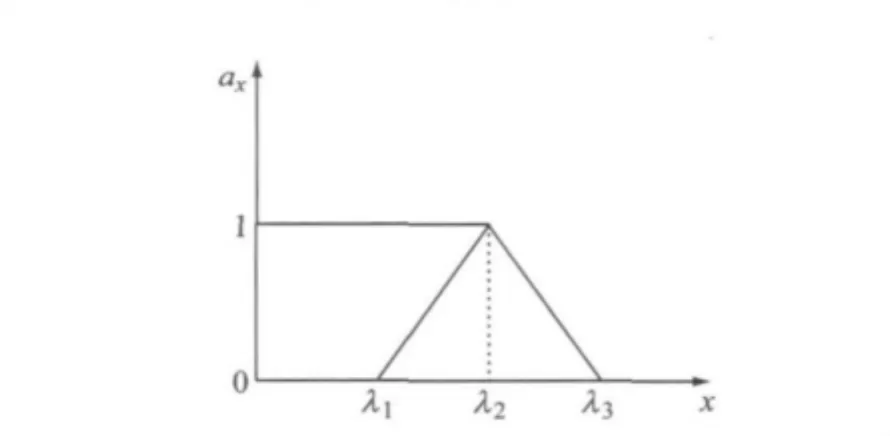
图1 隶属度函数分布Fig.1 The distribution of membership function

隶属度函数表达式

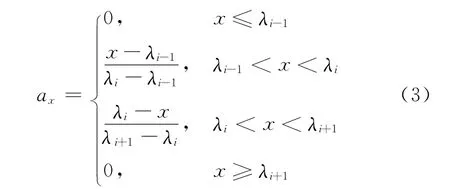
式中：x为风险指标值；λi－1，λi，λi＋1为风险等级临界值；ax为风险指标量测值对于风险等级i的隶属度.

确定了隶属度函数，就可以将实测数据代入函数，求出该数据的风险等级模糊评判矩阵.实际应用时，首先从二级指标开始，将一级指标中各二级指标的量测数据代入隶属度函数，求出模糊评判矩阵rij，rij＝［aij1aij2aij3aij4aij5］，从而该一级指标的模糊评判矩阵可由如下公式得到：

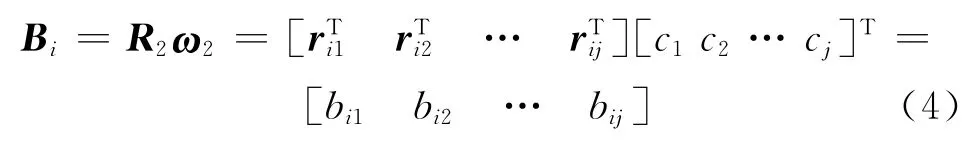
式中：ci为各二级指标权重值；rij为基于隶属度函数建立的模糊评判矩阵，表示一级指标i中的第j个二级指标对于各风险等级的隶属度；bij（i＝1，2，…，6；j＝1，2，…，5）为各一级指标的模糊评判值.

各一级指标的风险模糊评判矩阵计算出之后，就可以得到隧道当前整体风险模糊评判矩阵

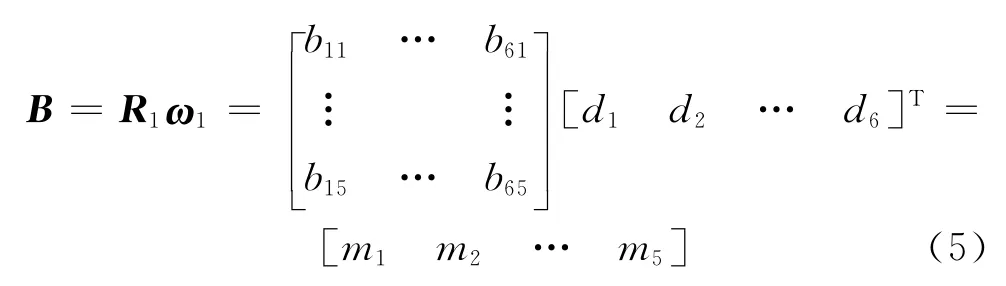
式中：di为各一级指标权重系数；mi为隧道施工风险指标对于风险等级i的隶属度.

1.4 动态风险指数

通常，对于计算出来的模糊评判矩阵B，认为m1～m5中的最大值所对应的风险等级即为计算出来的风险等级.为了将风险分析结论直观地表示，将前文所述的五个风险等级按百分制分别赋分（1级0分，2级30分，3级60分，4级80分，5级100分），通过模糊综合评判可以得到风险指标对于各个风险等级的隶属度，由此，可以得到隧道施工的动态风险指数

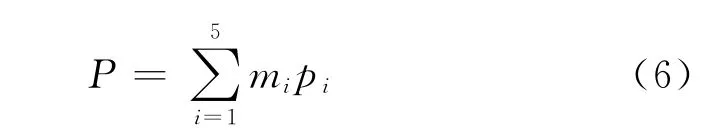
式中：pi为隧道施工风险等级赋分值.

由式（6）可见，动态风险指数最终被量化为一个百分数，而这个分数的大小反映了当前施工状态的风险等级，分数越高风险越大.

2 工程实例分析

石猴岭隧道为保阜高速公路隧道工程七座大型隧道之一，采用分离式隧道，新奥法施工.隧道部分以地下形式横穿山脊，围岩全部为Ⅴ级，穿越一个断裂带，断裂带由断层泥、构造碎裂岩构成，断裂影响带在黑云斜长片麻岩、混合岩化片麻岩之中，且该断裂走向与隧道走向几乎平行，并伴有裂隙水，对隧道稳定不利.因此，对隧道施工进行严密的量测，并进行动态风险分析.

2007年9月，石猴岭隧道右线已开挖至明暗洞交界处，按照前文所述的动态风险评估模型，将每天的量测数据代入，可以得到反映当前开挖风险的动态风险综合指数，9月—10月风险指数的动态变化如图2所示.

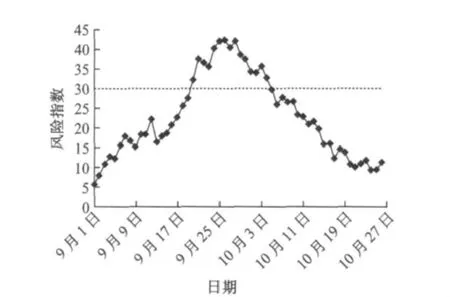
图2 石猴岭隧道2007年9月—10月动态风险指数变化Fig.2 Dynamic risk index from September to October 2007for Shihouling Tunnel

从图2可以看到，隧道开挖的风险一直增加，在9月25日附近，风险指数达到最大，风险较高.根据现场情况判断，主要是因为该开挖段山体位于一处断层上，导致现场围岩岩质软化且破碎严重，基本呈块石状，稍有扰动即呈现下滑状，并且地表沉降曲线出现反弯点，因此隧道主洞开挖存在极大的安全隐患，原有设计已不能确保隧道施工的安全.据此，业主联系设计单位和施工单位对原有设计进行更改，经协商后决定对原有设计做出变更如下：

（1）暗洞进口洞顶仰坡处φ22mm砂浆锚杆间距由原设计的1.2m×1.2m变更为1.0m×1.0m.

（2）K95＋900～K95＋916处超前管棚增加直径为50mm的超前小导管，规格及型号与原设计图纸相同，即仰角45°，纵向每排间距为4.0m，共增加4排，与原设计超前支护形成小三角支撑，以稳定围岩.

由图2可见，更改支护参数后10月份的动态风险指数呈下降趋势.这说明根据风险指数的动态变化及时调整设计施工参数，对降低施工风险、确保施工安全起到了重要作用.事实也证明更改支护参数后，开挖比较顺利，没有发生不安全事故.

3 结论

本文将新奥法施工量测体系与风险分析方法相结合，基于量测项目确定风险评价指标和评价体系，并采用层次分析法确定动态风险分析各指标的权重，进而利用模糊数学的隶属度函数理论，建立风险指标对于各风险等级的隶属度，最终通过归一化为统一的百分数，得到了施工过程的动态风险指数.该动态风险分析方法在保阜高速公路隧道工程施工过程中得到了应用.结果表明，本方法具有有效性和实用性，对于隧道开挖过程的风险变化能够及时、准确地反映，并能够对于主要致险因子进行辨别，这对于降低施工风险，减少事故发生概率具有明显作用.该方法简单、实用，值得进一步推广应用.

［1］ Einstein H H.Risk and risk analysis in rock engineering［J］.Tunneling and Underground Space Technology，1996，11（2）：14.

［2］ Einsten H H，Iindermiue C，Sinifeld J.Decision aids for tunneling［J］.Journal of the Transportation Research Board，1996，20（5）：6.

［3］ Sturk R，Olsson L，Johansson J.Risk and decision analysis for large underground projects，as applied to the Stockholm ring road tunnels［J］.Tunneling and Underground Space Technology，1996，11（2）：157.

［4］ Kampmann J，Eskesen S D，Sltnimers J W.Risk assessment helps select the contractor for the Copenhagen metro system［C］／／Proceedings of the World Tunnel Congress 98 on Tunnels and Metropolises.London：Taylor ＆Francis，1998，1：123－130.

［5］ You K，Park Y，Lee J S.Risk analysis for determination of a tunnel support pattern［J］.Tunneling and Underground Space Technology，2005，20（2）：479.

［6］ 李永盛，陶履彬，黄宏伟，等.崇明越江通道工程风险分析研究总报告［R］.上海：同济大学，2003.

LI Yongsheng，TAO Lvbin，HUANG Hongwei，et al.General report on risk assessment of the Chongming passages crossings Yangtze River［R］.Shanghai：Tongji University，2003.

［7］ 黄宏伟.隧道及地下工程建设中的风险管理研究进展［J］.地下空间与工程学报，2006，2（1）：13.

HUANG Hongwei.State of the art of the research on risk management in construction of tunnel and underground works［J］.Chinese Journal of Underground Space and Engineering，2006，2（1）：13.

［8］ 陈龙，黄宏伟.岩石隧道工程风险浅析［J］.岩石力学与工程学报，2005，24（1）：110.

CHEN Long，HUANG Hongwei.Risk analysis of rock tunnel engineering［J］.Journal of Rock Mechanics and Engineering，2005，24（1）：110.

［9］ 陈洁金，周峰，阳军生，等.山岭隧道塌方风险模糊层次分析［J］.岩土力学，2009，30（8）：2366.

CHEN Jiejin，ZHOU Feng，YANG Junsheng，et al.Fuzzy analytic hierarchy process for risk evaluation of collapse during construction of mountain tunnel［J］.Rock and Soil Mechanics，2009，30（8）：2366.

［10］ 王莲芬，许树柏.层次分析法引论［M］.北京：中国人民大学出版社，1990.

WANG Lianfen，XU Shubo.The introduction of AHP method［M］.Beijing：China Renmin University Press，1990.