蒙特卡罗方法数值模拟二维原子光刻

张萍萍，马 艳，李同保

（同济大学物理系，上海200092）

各种纳米级科学测量仪器，特别是作为纳米科技主要测量和操作工具的原子力显微镜（AFM）和扫描电子显微镜（SEM）等，由于受仪器工作原理、测量对象和环境因素影响，用不同仪器检测同一标样，或用同一仪器在不同环境下测量同一标样，结果可能截然不同.因此，研制准确适用的纳米计量传递标准是纳米科技中的关键问题［1］.利用激光驻波场原子沉积技术制作的一维原子纳米光栅，其周期直接溯源于原子跃迁频率，可用作纳米计量的标准.原子光刻技术是一种新型的沉积型光刻技术，采用激光场作为掩膜，准直好的中性原子在偶极力的作用下在基板上沉积，从而形成与光场形状一致的纳米结构.1993年，美国NIST的McClelland小组采用激光驻波场作为光场掩膜，制作出了实用的铬纳米光栅结构，光栅间距为212.6nm［2］.2011年，同济大学的李同保教授领导的原子光刻小组首次在国内制成了条纹清晰的纳米光栅，达到了实用性要求［3］.

一维纳米光栅在纳米计量应用中有其局限性，它只能在横向的一个维度内准直AFM以及SEM等测量仪器.而间距为λ／2（λ为激光波长）纳米点能在横向以及纵向同时准直上述测量仪器，大大提高了校正的精准度，因此，二维纳米点的制作能进一步推动纳米计量的发展.美国NIST的McClelland小组［4］以及德国康斯坦茨大学Pfau小组［5］，利用偏振方向平行于光场平面的正交激光驻波场形成的相位恒定的光格点，制作出了间距为λ／2铬纳米点.McClelland等利用粒子光学模型［6－11］，分析了激光功率、失谐、束腰半径等实验参数对纳米光栅沉积条纹的半高宽、对比度的影响，对纳米光栅的实验研究具有很好的指导作用.本文基于粒子光学模型，采用蒙特卡罗方法确定初始条件，数值分析不同激光功率、横向发散角以及基板位置下的正交激光驻波场的沉积与汇聚特性以及纳米点的三维结构，为纳米点的研制提供较好的理论基础.

1 理论模型

激光驻波场汇聚铬原子沉积如图1所示［2］.从高温原子炉中蒸发出来的铬原子束，经由横向激光束多普勒或亚多普勒冷却后，通过由激光驻波场形成的原子透镜时，原子会在驻波场偶极力的作用下向低势阱处（蓝失谐）或高势阱处（红失谐）会聚，从而在基片上沉积形成周期性纳米结构，周期为λ／2.

图1 激光驻波场汇集铬原子沉积示意图Fig.1 Geometry for laser－focused atomic deposition

在一维原子光刻中，光场掩膜为高斯型激光驻波场，而间距为λ／2的正方形纳米点的光场掩膜为偏振方向平行于光场平面、正交的高斯激光驻波场形成的相位恒定的二维光格点，其光场配置以及实验设置均已在文献［5］中给出.假设原子束沿OZ轴运动，正交激光驻波场光强分布于XOY平面，那么高斯型二维光格点光强的分布可以表示为［4］

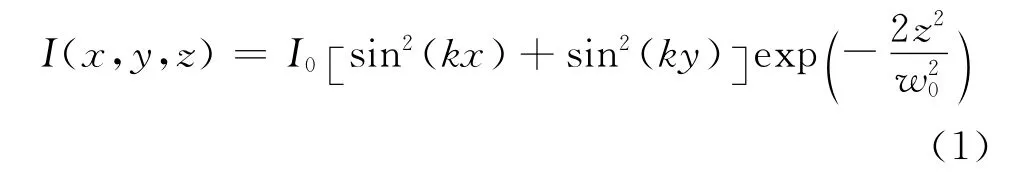
式中：k＝2π／λ，I0为高斯中心处光强，w0为束腰半径.

基态原子在激光场中的光学势能为

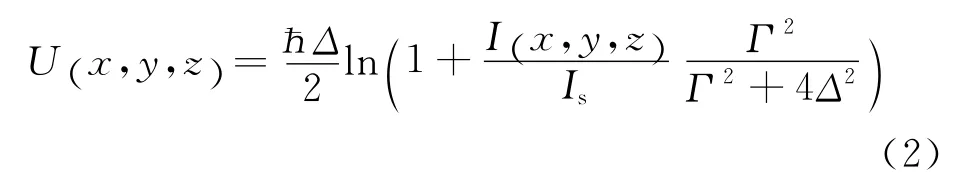
式中：ħ＝h／2π（h为普朗克常量），Δ为失谐，Γ为自发辐射率，Is为饱和激光光强.

原子在三维激光驻波场中的运动轨迹方程可以表示为［12］

式中：α为原子束OX方向初始发散角；β为原子束OY方向初始发散角；E0＝mv2／2，m为原子质量，v为原子沿OZ轴的纵向速度.

使用（xi，yi，vi，αi，βi，Ti）表示每条轨迹的初始条件［11］，其中xi，yi表示原子进入光场的初始位置.如果对n个周期内的沉积进行模拟，那么xi，yi应选择［0，0.5nλ］当中的随机数.vi表示初始纵向速度，αi，βi分别表示原子束OX，OY方向初始发散角.原子纵向速度vi满足麦克斯韦－玻耳兹曼分布律，横向发散角αi符合高斯分布，两者符合联合概率密度分布函数［6］

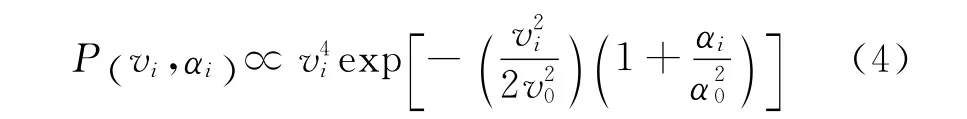
Ti表示所选取的原子是否为与光场发生作用的52Cr原子.铬元素各自然同位素中，52Cr原子的丰度为84%左右，剩下的同位素如53Cr，54Cr等总和只占16%，不与光场发生作用.首先选取均匀分布于［0，1］之间的随机数r，如果r∈［0.16，1.00］，那么可以认为此时产生的原子为52Cr，三维空间的原子轨迹方程按式（3）来计算；如果r∈［0，0.16），此时认为原子的属性为52Cr的同位素.由于同位素不与光场耦合，本文中亦忽视重力的作用，故同位素的运动轨迹应是一条直线，其运动轨迹应满足微分方程组

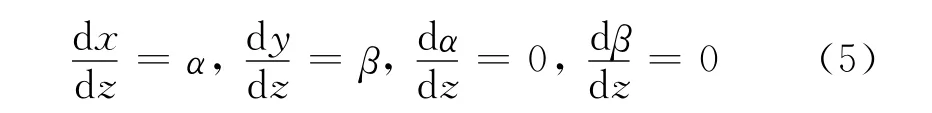
通过蒙特卡罗方法确定了每条轨迹的初始条件（xi，yi，vi，αi，βi，Ti）之后，即可通过轨迹方程（3）或（5）来追踪原子运动，从而得出沉积平面处原子密度的分布情况.

2 模拟结果

2.1 模拟参数

在以下仿真计算过程中，使用的相关参数如下：52Cr原子能级跃迁7S3→7对应的波长λ＝425.55nm，自发辐射率Γ＝5×2πMHz，饱和光强Is＝85mW·cm－2；汇聚激光束入射功率P＝20 mW，失谐Δ＝－200×2πMHz，束腰半径w0＝60 μm；原子炉温度t＝1 550°C，所对应的最可几速度v0≈950m·s－1；二维准直后的铬原子束横向、纵向发散角半高宽均选取αFWHM＝0.16mrad［13］.在本文的模拟中，均不考虑基板衍射对光场的影响.图2给出了二维光格点的势阱.在偶极力的作用下，原子将在基板沉积形成与光场一致的纳米结构.

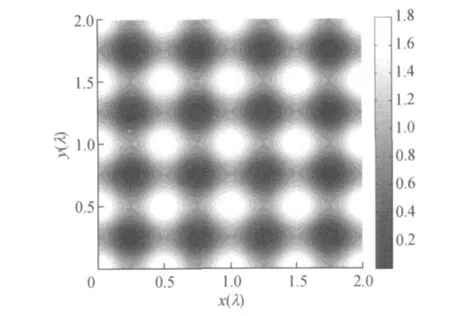
图2 二维光格点势阱Fig.2 Optical potential for 2Doptical lattice

2.2 激光功率对纳米点的影响

图3显示了2λ×2λ区域内不同激光功率下的沉积结构.采用2.1节提供的参数，基板位于z＝0处，沉积原子数为500 000.当激光功率分别为5，10，20，40mW时，所得纳米点高度分别为2.1，2.9， 5.2，3.6nm，半高宽分别为62，43，35，51nm.当前参数下，当激光功率为20mW时，纳米点的质量最好.在原子光刻中，激光功率对沉积的影响是通过薄透镜模型、厚透镜模型及沟道化模型等三种沉积模型来实现.在薄透镜情形下，汇聚激光功率较小，原子束的聚焦平面在激光场外；在厚透镜情况下，汇聚激光功率较大，原子束的聚焦平面在激光场内，而沟道化模型则有可能形成多个聚焦平面.由式（1）可知，偏振方向平行于光场平面、正交激光驻波场形成的光格点的光强为两束激光驻波场光强的线性叠加，因此，一维原子光刻中的原子透镜理论完全适用于正方形纳米格点的沉积.依据文献［3］所提出的一级傍轴近似汇聚功率公式Pfocus＝aπE0IsΔ／（ħΓ2k2）（其中a为激发参数）可以判定，在当前参数下，5 mW所对应的原子透镜模型为薄透镜模型，10，20 mW所对应的模型为厚透镜模型，40mW为沟道化模型.5mW所对应的是薄透镜模型，沉积质量较差是因为聚焦平面与基板平面相距较远；10，20mW应是厚透镜模型，此时聚焦平面与基板平面相距较近，故沉积质量较好；40mW所对应的厚透镜模型具有沟道化效应，在高斯光束内具有多个聚焦平面，此时沉积质量亦较好.图4显示了激光功率对纳米点质量的影响.可以看出，在厚透镜与沟道化区域，半高宽较小，高度较大.因此，实验最好在厚透镜与沟道化区域进行.

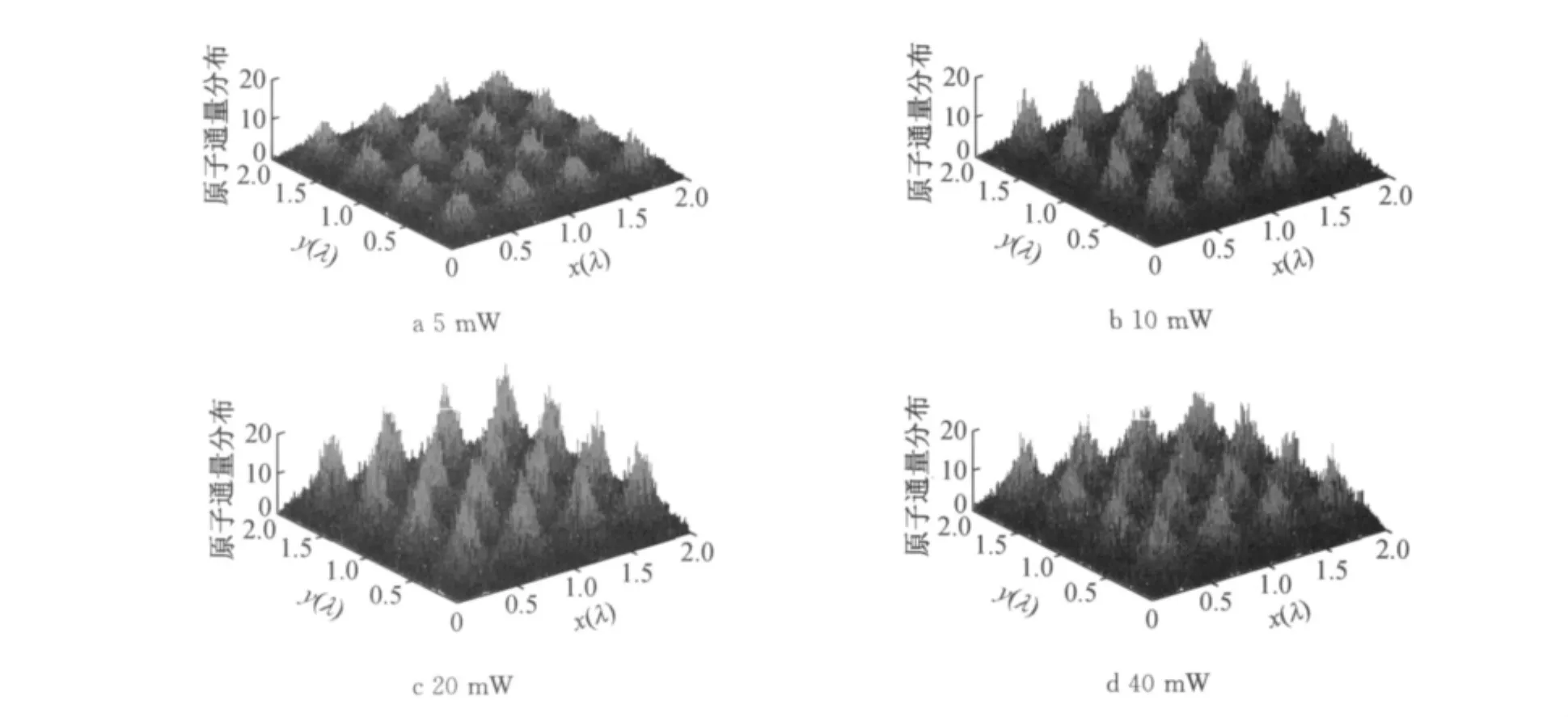
图3 不同激光功率下纳米点三维结构Fig.3 3Dstructures of nanodots under different laser powers

2.3 横向发散角对纳米点的影响

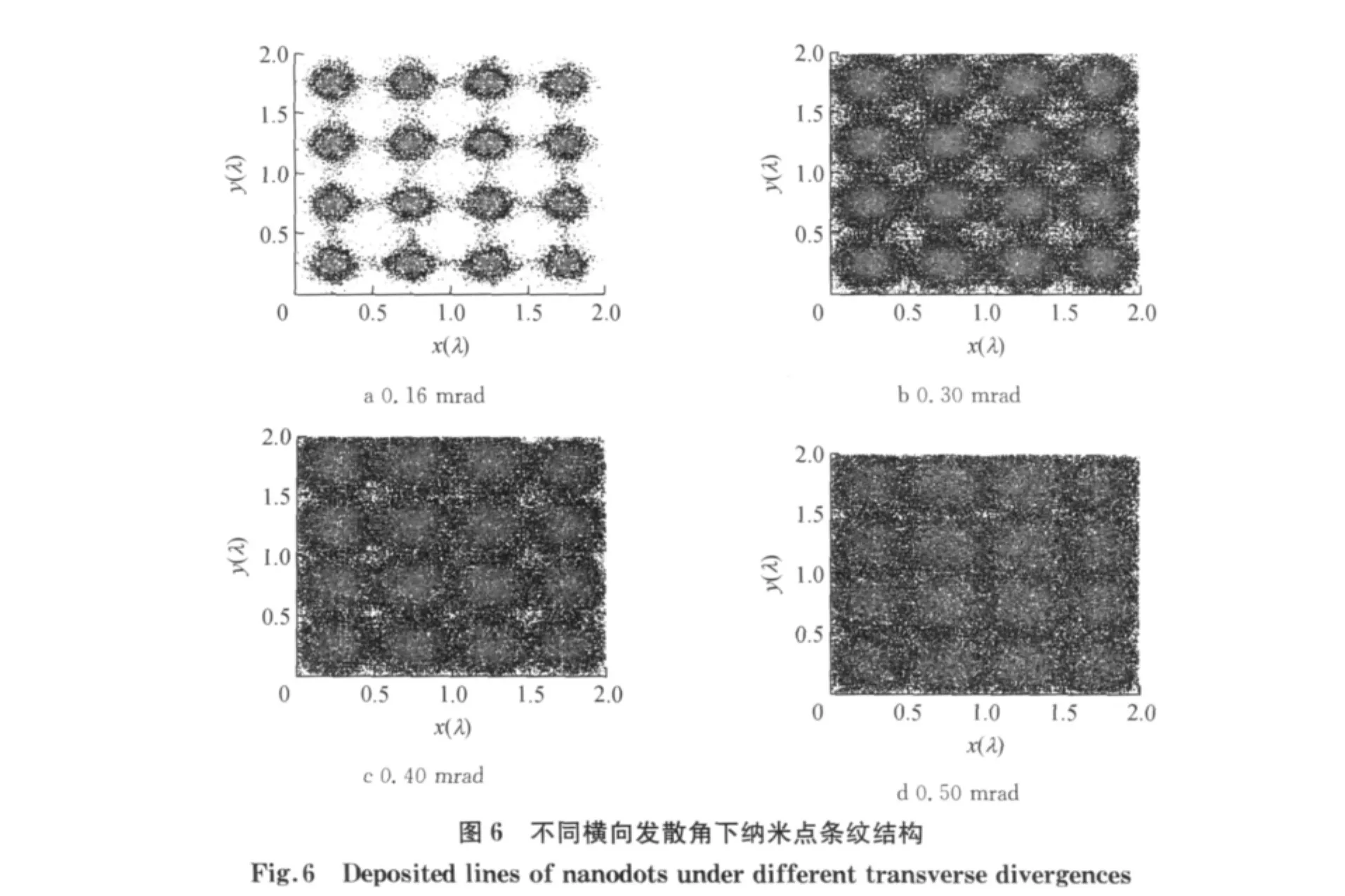
一维原子光刻中，理论与实验结果均表明，激光准直后铬原子束的横向发散角对沉积后的纳米光栅结构具有决定性的影响.为此，分析横向发散角对二维纳米点微结构的影响至关重要.图5显示了2λ× 2λ区域内不同横向发散角情况下二维纳米点的三维结构，图6为图5三维结构的投影.采用2.1节所提供的参数，激光功率为20mW.基板位于高斯激光中心z＝0处，沉积原子数500 000.当横向发散角分别为0.16，0.30，0.40，0.50mrad时，所得纳米点微结构的高度分别为5.2，2.5，2.0，1.0nm，半高宽分别为35，61，124，180nm.随着横向发散角的增加，纳米点的高度显著降低，半高宽急剧增加.这是因为当发散角增加时，原子透镜的轴外像差增加，这就使得焦点扩散，如图6所示.当横向发散角大于0.40mrad时，几乎看不出纳米点的周期结构.为此，在二维原子光刻实验中，应尽可能减小横向发散角.

图4 激光功率对纳米点质量的影响Fig.4 Effect of laser power on characteristics of nanodots

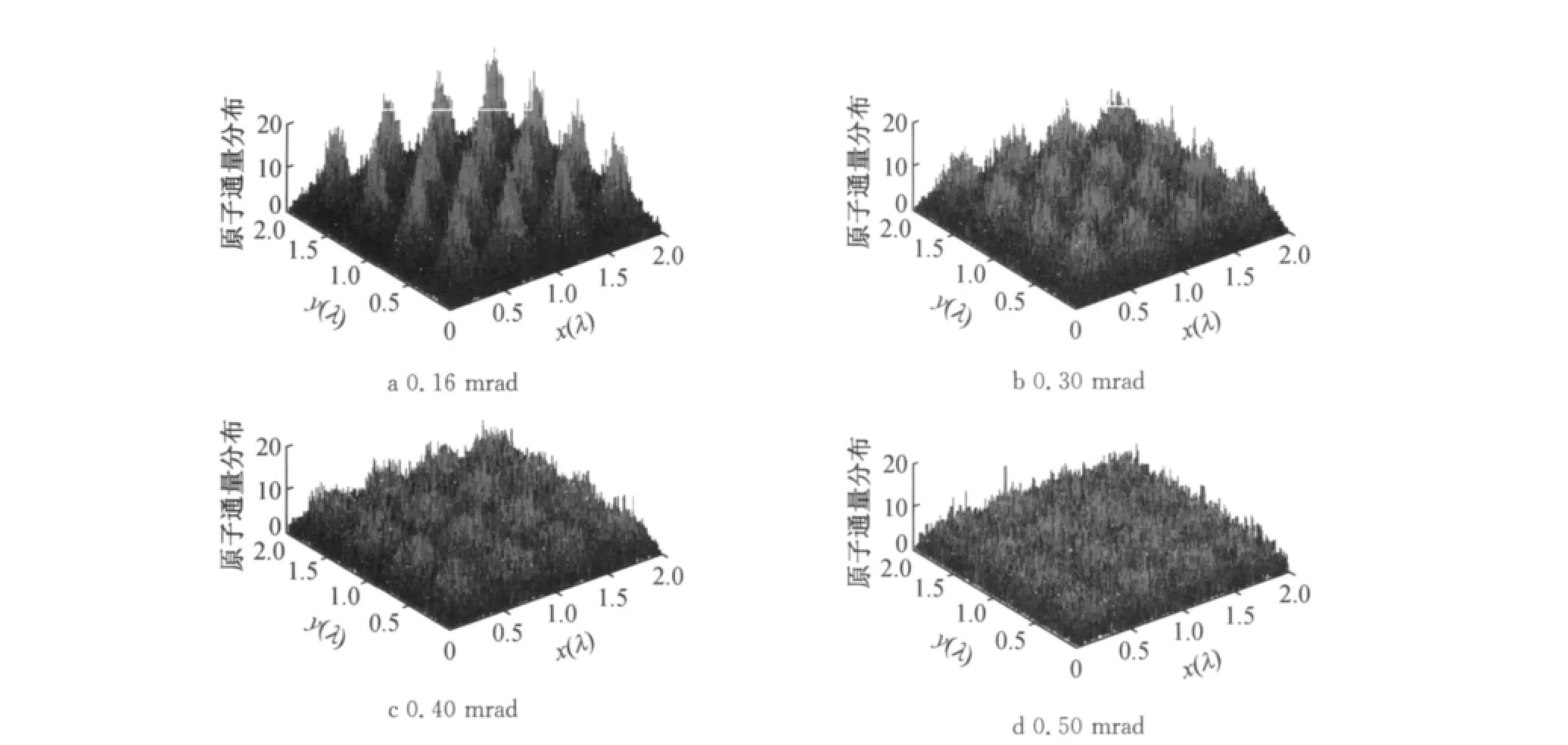
图5 不同横向发散角下纳米点三维结构Fig.5 3Dstructures of nanodots under different transverse divergences

2.4 基板位置对纳米点的影响

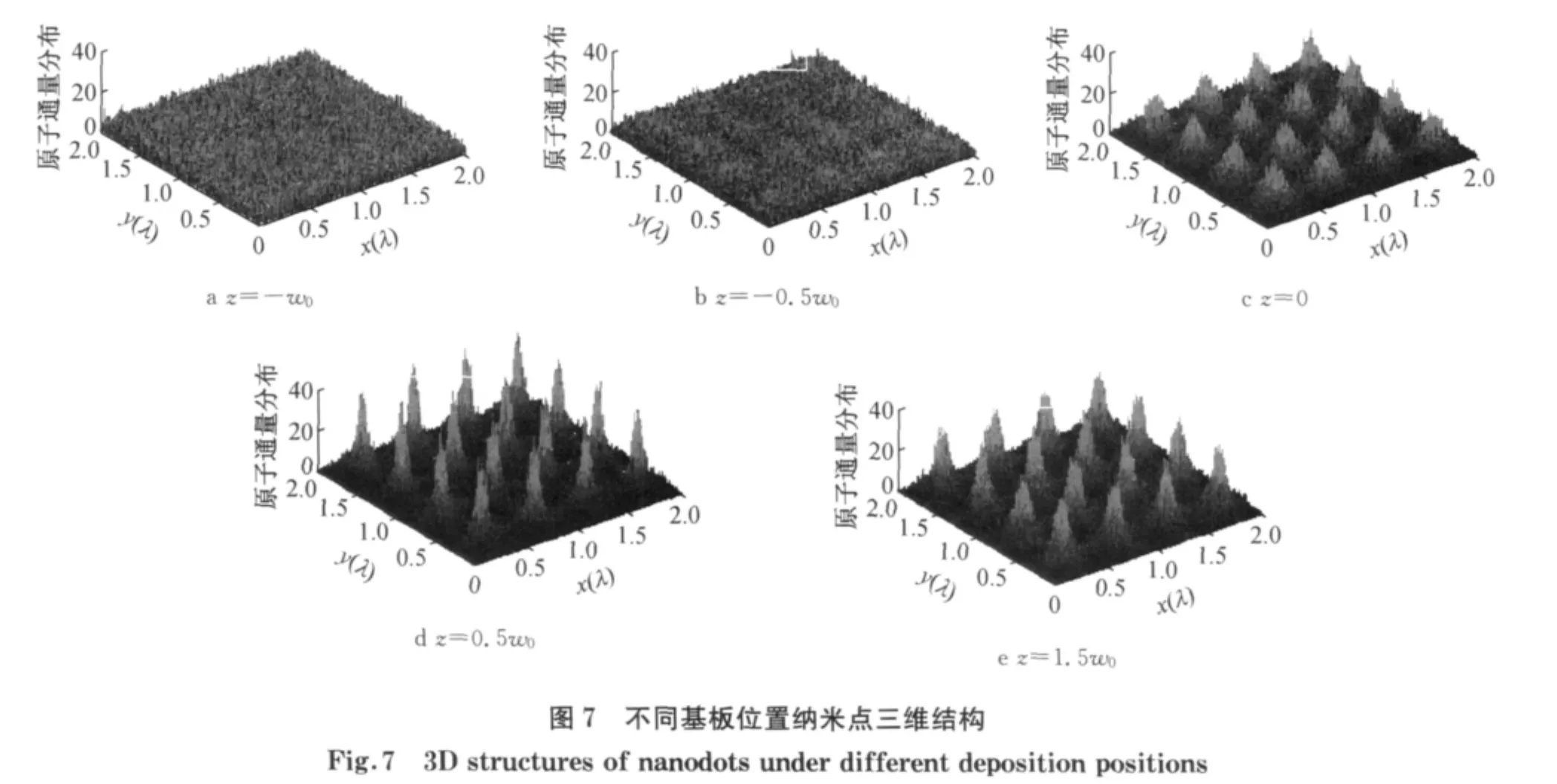
图7显示不同基板位置处纳米点的三维结构，设激光功率P＝20mW，其余参数与2.1节相同，在2λ×2λ的区域内，沉积原子数为500 000.如图7a，b所示，当基板位置为z＝－w0，－0.5w0时，看不出明显的周期性纳米结构.当基板位置为z＝0，0.5w0，1.5w0时，纳米结构高度分别为5.2，10.4， 6.2nm，半高宽分别为35，24，30nm.可看出，纳米点的质量随基板位置的变化而剧烈变化.这是因为在当前参数下，原子透镜的焦点在z＝0.5w0处附近，此时得到的纳米点特征最好.当基板位置远离焦点时，纳米点的特征逐渐变差.因此在实验中，在基板衍射影响较小的情况下，基板位置应尽量与原子透镜的焦点重合，这样有利于得到特征较好的纳米点.

3 结论

本文基于粒子光学，采用蒙特卡罗方法确定初始条件，数值分析偏振方向平行于光场平面的正交激光驻波场的汇聚与沉积特性.在2λ×2λ的区域内得到间距为半波长的纳米点，同时分析激光功率、横向发散角及基板位置对沉积结构的影响.模拟结果表明，当激光功率为20mW时，所得纳米点的质量最高.与一维原子光刻类似，横向发散角与基板位置放置对纳米点质量具有较大影响.为此，在实验中，应尽可能减小横向发散角，并应选取合适的基板位置.

［1］ 李同保.纳米计量与传递标准［J］.上海计量测试，2005，32（1）：8.

LI Tongbao.Nanometrology and transfer standard［J］.Shanghai Measurement and Testing，2005，32（1）：8.

［2］ McClelland J J，Shorten R E，Palm E C，et al.Laser－focused atomic deposition［J］.Science，1993，262（5135）：877.

［3］ MA Yan，LI Tongbao，WU Wen，et al.Laser－focused atomic deposition for nanoscale grating［J］.China Physics Letters，2011，28（7）：073202.

［4］ Gupta R，McClelland J J，Jabbour Z J，et al.Nanofabrication of a two－dimensional array using laser－focused atomic deposition［J］.Applied Physics Letters，1995，67（10）：1378.

［5］ Schulze Th，Brezger B，Mertens R，et al.Writing a superlattice with light forces［J］.Applied Physics B，2000，70（5）：671.

［6］ McClelland J J.Atom optical properties of a standing－wave light field［J］.Journal of the Optical Society of America B，1995，12（10）：1761.

［7］ Anderson W R，Brandley C C，McClelland J J，et al.Minimizing feature width in atom optically fabricated chromium nanostructures［J］.Physical Review A，1999，59（3）：2476.

［8］ Jurdík E.Laser manipulation of atoms and nanofabrication［R］.Leuven：Katholieke Universiteit Leuven，2001.

［9］ CHEN Xianzhong，YAO Hanmin，CHEN Xunan.Classical simulation of atomic beam focusing and deposition for atom lithography［J］.Chinese Optics Letters，2004，2（4）：187.

［10］ 张宝武，马艳，李同保，等.激光功率对铬原子束一维沉积的影响［J］.光学学报，2009，29（2）：421.

ZHANG Baowu，MA Yan，LI Tongbao，et al.Effect of laser power on one－dimensional deposition of chromium atomic beam［J］.Acta Optica Sinica，2009，29（2）：421.

［11］ 张萍萍，马艳，李同保.一维原子光刻经典模型的优化［J］.光学学报，2011，31（5）：0514004.

ZHANG Pingping，MA Yan，LI Tongbao.Optimization of particle optics model for 1D atom lithography［J］.Acta Optica Sinica，2011，31（5）：0514004.

［12］ Okamoto K，Inouye Y，Kawata S.Atomic－beam propagation in a two－dimensional standing wave of light：a numerical analysis based on a particle－optics［J］.Japanese Journal of Applied Physics，2001，40（2A）：609.

［13］ Scholten R E，Gupte R，McClelland J J，et al.Laser collimation of a chromium beam［J］.Physical Review A，1997，55（2）：1331.