道面状态转移概率估计的混合效应模型
刘玉海,凌建明,杜 浩
(同济大学道路与交通工程教育部重点实验室,上海201804)
马尔可夫过程是当前应用最广泛的道面使用性能概率预测模型,能够以概率的形式模拟道面使用性能的随机衰变特征,其核心内容是确定状态转移概率矩阵.对机场道面而言,不同的道面结构、使用时间、区域环境以及交通量水平具有不同的使用性能衰减特征,其状态转移概率矩阵也是不同的[1].传统建立状态转移概率矩阵的方法,主要包括经验统计方法、回归方法以及非线性优化方法等[2],虽在一定的条件下能满足工程要求,但随研究深入其不足之处日益受到关注.传统方法均以静态转移过程假设为前提,认为马尔可夫转移概率矩阵不随时间变化而变化,与实际衰变模式不符.此外,通常不考虑道面结构、环境因素、交通荷载以及其他相关因素对状态转移概率矩阵的影响,只对单个道面或道面族建模,即以道面性能时间序列数据为样本建立指标与使用时间或轴载作用次数的一元回归关系,但需要多年观测数据,对于改(扩)建或大修道面,大多难以实现.如果综合利用多个道面观测数据,必须尽量将各类影响因素作为解释变量纳入回归方程中分解误差成分,以降低多道面样本数据回归分析时的残差相关性,从而建立性能指标与因素变量之间的多元回归关系.但普通多元回归只能分析连续变量,无法考虑分类变量(如结构类型、养护水平等)和随机观测误差的影响.
针对马尔可夫模型的缺陷,国内外学者做了很多研究工作.Butt[3]将分析期(30年)分为五段,采用传统方法分别建立转移概率矩阵.Madanat等将计量经济学中Probit模型[4]和Poisson回归模型[5]引入设施管理技术中,建立设施性能影响变量与转移概率之间的回归关系,得到动态转移概率矩阵.Mishalani等[6]采用持续时间模型估计基础设施状态转移概率.Yang等[7]采用二分类Logistic回归模型,考虑养护水平、道路使用时间、交通量等因素与沥青路面开裂概率的线性关系,得到动态反馈马尔可夫转移概率矩阵,实现沥青路面开裂指数的概率预测.Li利用AASHTO测试数据,采用次序Probit模型建立路面使用性能动态概率预测模型[8].Chua等[9]以路面材料疲劳模型为基础,通过分析结构失效率,建立状态转移概率矩阵.虽然以上概率方法通过多元回归技术,同时将连续变量和分类变量纳入到模型中,分析多因素对道面使用性能的影响,建立道面使用性能状态转移概率与因素变量之间的总体平均模型,进一步提高多元回归模型的精度,但无法考虑不同区域多个道面之间和单个道面内可观测自变量无法解释的潜在随机误差,忽视总体期望与个体特性的差异,从而影响估计精度[10].尤其在构建国内机场道面使用性能概率预测模型时,观测数据覆盖面广、离散性高、连续性差,既要考虑针对单个道面建模时观测时间序列数据不足和采用传统方法的困难,又要考虑采用不同区域多个道面的观测数据交叉建模时,如何减少来自多个抽样总体的数据间不可观测的异质性.因此,本文将借鉴前人研究成果,以Logistic回归模型为基础,考虑随机效应作用,采用广义线性混合效应模型对多道面数据进行拟合分析,降低总体异质性,构建动态马尔可夫状态转移概率矩阵,以达到更好的预测效果.
1 状态转移概率矩阵
假设系统所处的状态有n种,任意时刻系统处于各种状态的概率分布记为
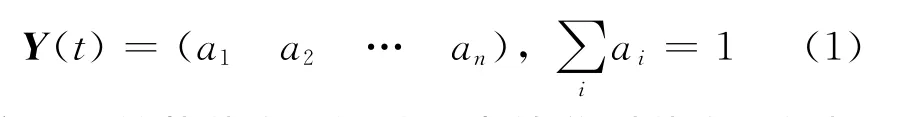
定义系统从状态i经过一步转移到状态j的概率为一步转移概率,那么具有n种状态的系统转移概率就构成了系统转移概率矩阵P,其形式如下:

为了较好地反映机场道面使用性能的衰变过程,将道面PCI离散为由优、良、中、次、差(1~5)五个状态组成的状态空间.然后确定每个状态对应的区间及区间中值,并作如下假设:在日常维修养护条件下,道面使用性能由低水平状态向高水平状态转移的情况不会发生,即当i>j时pij=0;在一年时间以内其使用性能等级不会下降太快,可近似认为道面使用性能衰变只发生在两个等级之间,即当(j-1)≥2时pij=0.道面状态转移概率矩阵可表示为

2 普通和混合效应Logistic模型的建立
2.1 普通Logistic模型的建立[11]
假设在一定外界条件的影响下,有一个理论上存在的连续反应变量Uin,其值域为负无穷至正无穷.该连续反应变量与外界影响的关系是线性的、确定的,满足线性模型
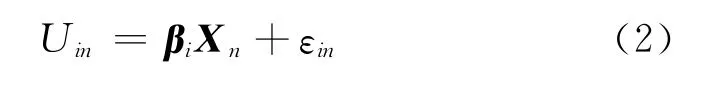
式中:Uin为道面区域n在状态i时的虚拟变量,它反映观测对象状态变化的内在趋势,但并不能被直接观测或测量;Xn是道面区域n的外界影响因素向量,也是自变量;βi是状态i下的回归方程系数向量;εin是误差项.
由于虚拟变量无法测量,因此无法直接对以上回归方程进行估计,但在每一时刻道面所处的状态等级,以及观测周期内道面状态等级的变化是可以观测到的.设yin为道面状态等级发生转移的指示变量,如果道面状态等级在一定的时间周期内由i状态变化为j状态,则yin记录该事件的发生,yin=ji.由于道面使用性能状态的转移只发生在两个等级之间,对于任意一个道面单元,经历一年的使用后,其使用性能要么仍停留在原来状态等级,要么衰变到下一个状态等级,由此构成了两种状态的二分类问题.Uin代表事件发生的概率,当该变量的值跨越临界点c,便导致事件发生.为了计算方便,通常取c=0,于是有
情况1:当Uin≤0,yin=0代表事件未发生,即道面性能状态未发生转移.
情况2:当Uin>0,yin=1代表事件发生,即道面性能状态发生转移.
可得到事件发生的概率为
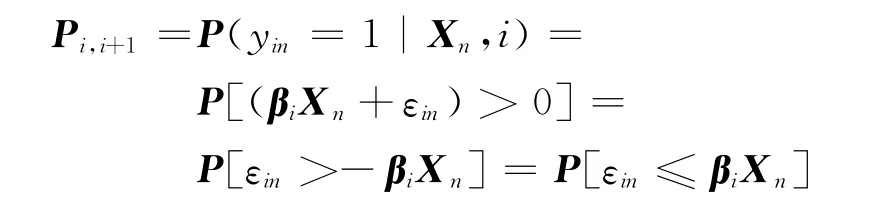
假设误差项εin服从Logistic分布,即分布函数如下式所示:
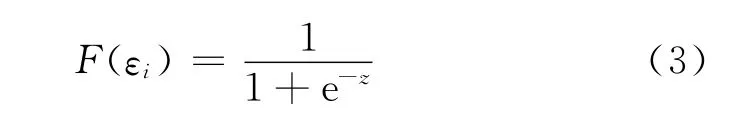
则道面使用性能状态发生转移和不发生转移的概率为
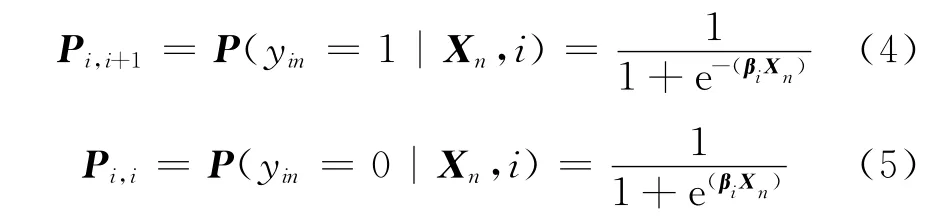
由于Logistic模型是一种广义的线性模型,具有非线性模型特征,因此,该模型的参数估计采用极大似然法.借助于计算机程序实现参数βi的估计,将其代入到式(4)或(5)中可获得道面不同状态下转移概率.
2.2 混合效应Logistic模型的建立
回归模型中的误差项εin至少可分为两个层面,即多个道面或道面族之间结构参数、环境因素、交通荷载等自变量观测引起的层间误差以及单个道面使用性能时间序列数据观测的层内误差.普通Logistic回归模型对此没有选择,只能分析可观测的自变量对应变量的固定效应,加大了残差成分的相关性,影响模型精度.混合效应Logistic模型认为回归系数是随机变动的,个体模型的回归系数是总体模型随机的样本,将随机效应引入模型参数中.模型中同时包含了固定效应和随机效应,固定效应反映了可观测的自变量对应变量的固定影响,而随机效应反映个体内和个体间不可观测的变异,进一步分解总体方差,可以提高精度.混合效应Logistic回归模型[12]的基本形式为

式中:X,Z分别为固定效应和随机效应设计矩阵;β,b为模型的固定效应和随机效应参数向量,认为随机效应b满足均值为零、方差矩阵为G的正态分布,记为bi~N(0,G).当随机效应不存在时,线性混合效应模型就退化为线性模型.
需要指出的是,混合效应模型采用迭代估计算法,不仅可得到固定效应估计值建立总体平均模型,还可以得到随机效应bi估计值^bi,实现数据源中任意个体道面的性能预测.不但减少了传统建模方法的工作量,而且克服了少数道面个体因观测数据不足带来的建模困难.
3 模型应用分析
3.1 模型函数
为介绍混合效应Logistic回归模型应用方法.采用我国华东区机场水泥道面实测PCI数据进行分析.考虑到机场所处的气候环境和养护水平相似、道面结构类型相同,根据数据组信息,以道面结构厚度、年起降架次、道面使用时间以及当前等级状态为解释变量建立Logistic模型函数,如下式所示:
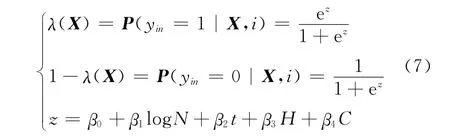
式中:β0,β1,β2,β3,β4为模型参数;N为年起降架次;H为道面结构厚度,cm;t为道面使用年限,a;C为道面当前所处的状态等级.
混合效应Logistic模型是普通Logistic模型的延伸,通常有两类混合效应Logistic回归模型可以被拟合,一类是随机截距模型,一类是随机截距和随机系数模型.结合以上分析,分别建立两类混合效应Logistic回归模型如下:
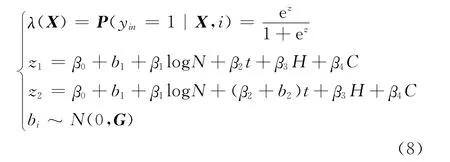
3.2 参数估计结果分析
以16组刚性道面PCI观测数据为基础,采用统计软件实现混合效应Logistic回归模型的参数估计,分别得到两类效应模型的参数估计结果及精度检验结果,如表1,2所示.表中拟合优度统计量分别为:似然值对数(-2Log Likelihood)、赤池信息(AIC)、改进赤池信息(AICC)、贝叶斯信息(BIC)以及分别由Cox &Snell,Nagelkerke提出的类R2统计指标.
由表1可见,两类模型中固定效应均有统计学意义,且估计值非常接近.而随机截距和斜率模型中随机截距项b0有统计学意义,但时间变量的随机斜率b1没有统计意义,概率为0.823 7,说明个体模型在时间系数上没有显著差异但个体间存在异质性,而且该异质性可由个体随机效应进行解释.显然普通Logistic回归模型无法对误差项进行分解,通常一些与自变量相关的随机系数项直接进入残差中,从而导致残差相关,违背残差独立同分布的假设,进而影响模型参数估计可靠性和预测结果.
表2中数据表明,混合效应Logistic模型的拟合优度统计量AIC,AICC和BIC越小则拟合越优,-2Log Likelihood相同.结合随机效应参数估计结果,认为随机截距模型更佳.
由表1中固定效应估计结果得到道面性能状态发生转移的优势比为

截距β0为基准优势比的对数,即没有任何变量存在时所产生的优势比,exp(β0)=0.003说明在无固定效应影响下道面状态将以极小的优势比例发生转移.β1=2.239为交通量变化系数,系数符号为正且exp(β1)=9.384,说明年起降架次每增加10倍,道面使用性能状态发生转移的概率优势将增加9.384倍.与此相反,道面厚度系数β3=-0.187符号为负且exp(β3)=0.829,即道面面层厚度每增加1cm时,相应的状态转移发生优势比例将下降0.829倍.C回归系数符号为负,反映了道面由高等级状态向低等级状态转移的趋势和规律.
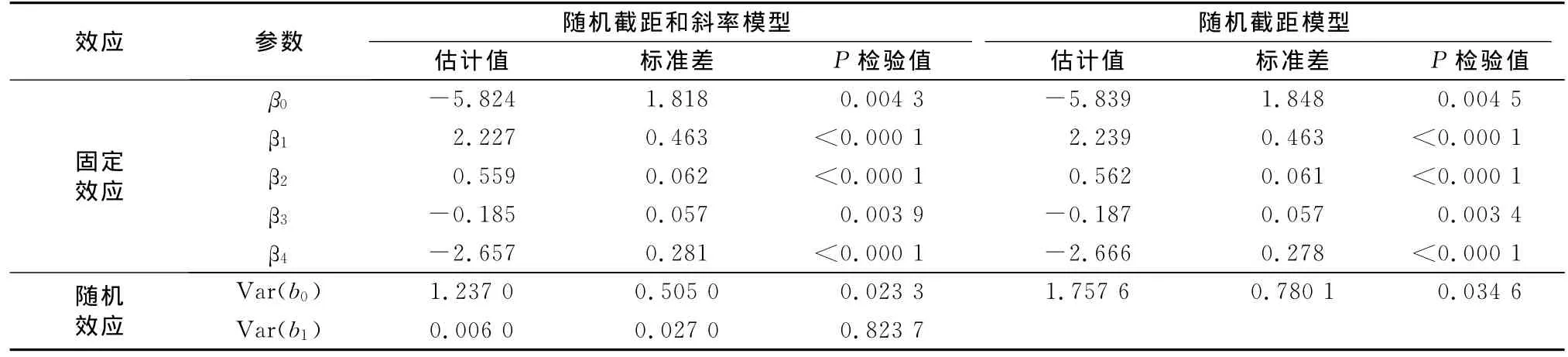
表1 两类混合模型的参数估计结果Tab.1 Parameter estimation for effect of two mixed Logistic models

表2 两类混合模型的拟合优度检验表Tab.2 Goodness-of-fit test of two mixed effects Logistic model
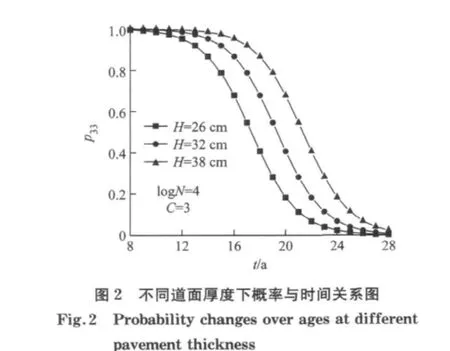
图1和图2给出了三种不同交通量和道面厚度条件下,道面使用性能在等级3状态下的转移概率随时间变化关系图.如图可见,道面衰变速率随交通量增加而加快,随道面厚度的增加而相应减慢;道面状态发生转移的概率随道面使用时间的增长而逐渐增大,直至道面由当前状态全部下降到一个状态,与道面性能实际衰变规律相符.
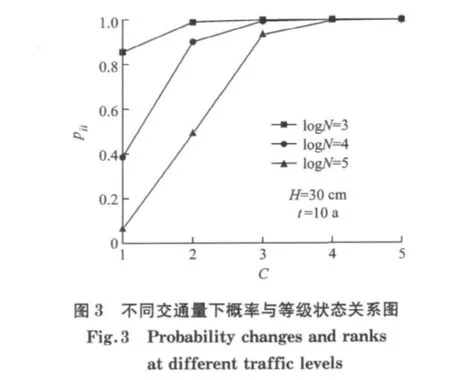
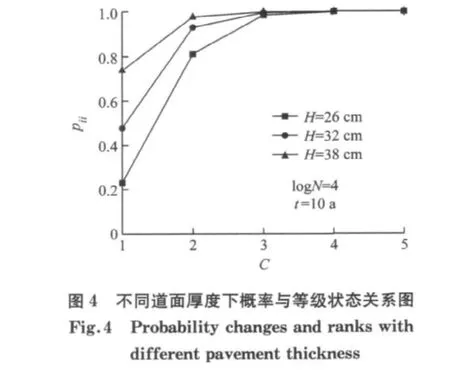
图3和图4为不同交通量和道面厚度下,道面性能状态不发生变化的概率与状态等级关系图.从图中可见,道面性能状态越优时,转移概率越大,反映道面状态由高等级逐渐向低等级发生转移的过程.同时由于道面处于低等级状态时日常养护活动的干预,降低了道面状态转移的概率.
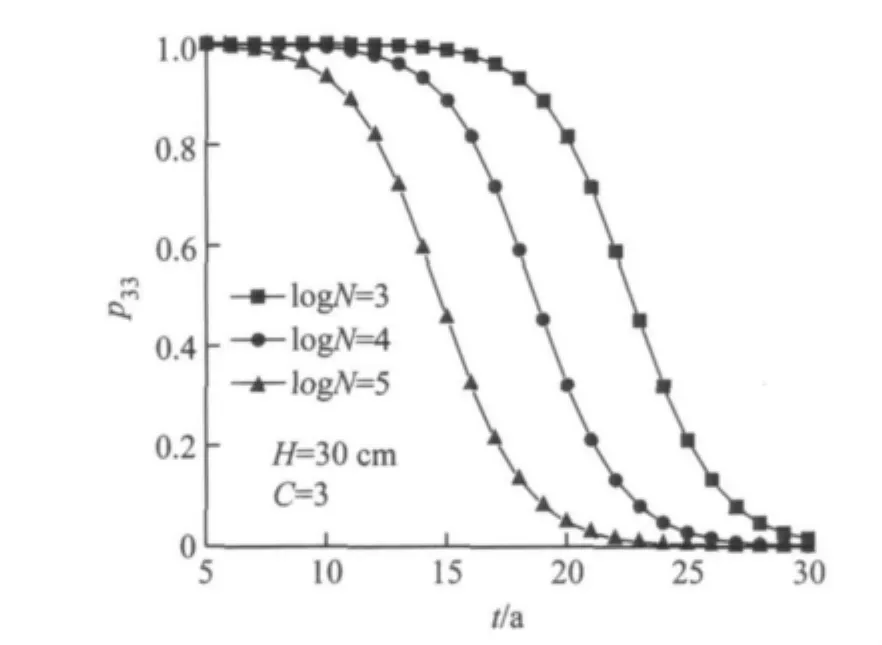
图1 不同交通量下概率与时间关系图Fig.1 Probability changes over ages at different traffic levels
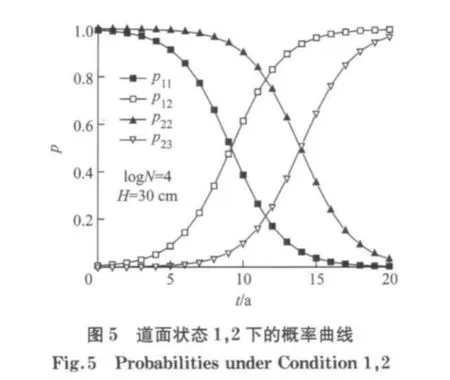
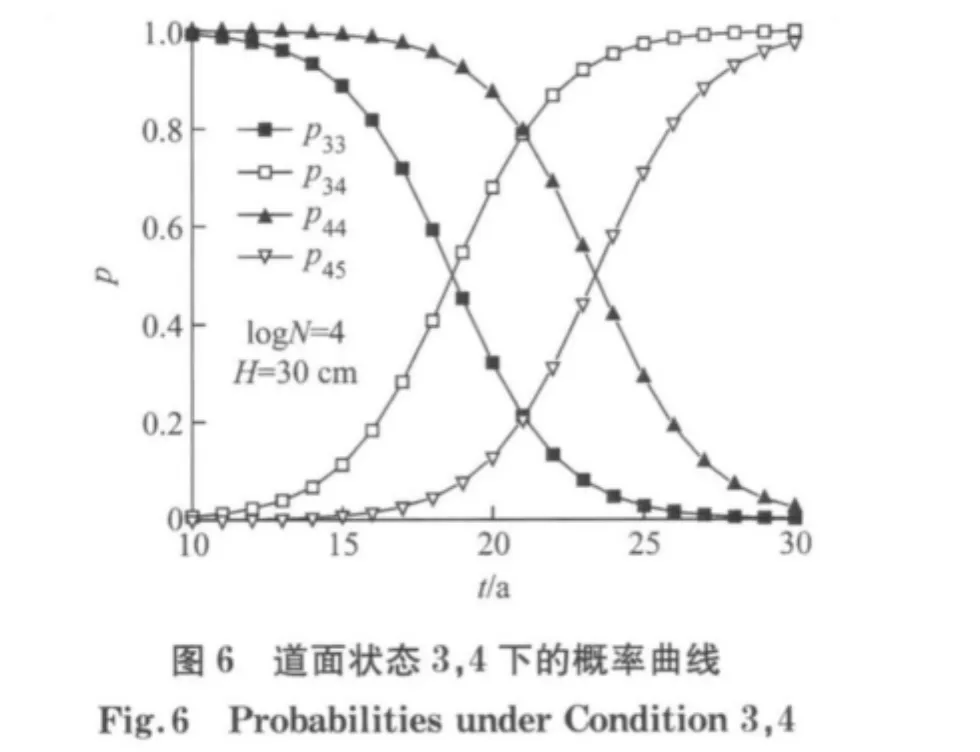
图5和图6为道面状态概率曲线图,由图可见各等级上道面使用性能状态转移概率随时间的动态变化呈相似的非线性特征,其主要差异体现为状态发生显著变化时所对应时间区间不同.这一点符合道面使用性能等级划分及逐步递减的规律.由概率曲线可获得任意时刻和状态下道面状态变化的概率值,从而确定动态马尔可夫状态转移概率矩阵.
3.3 拟合效果分析
为分析混合效应Logistic回归模型的应用效果和优势,将其与普通Logistic回归模型进行对比.采用同一组数据源估计式(9)中模型参数如表3所示.
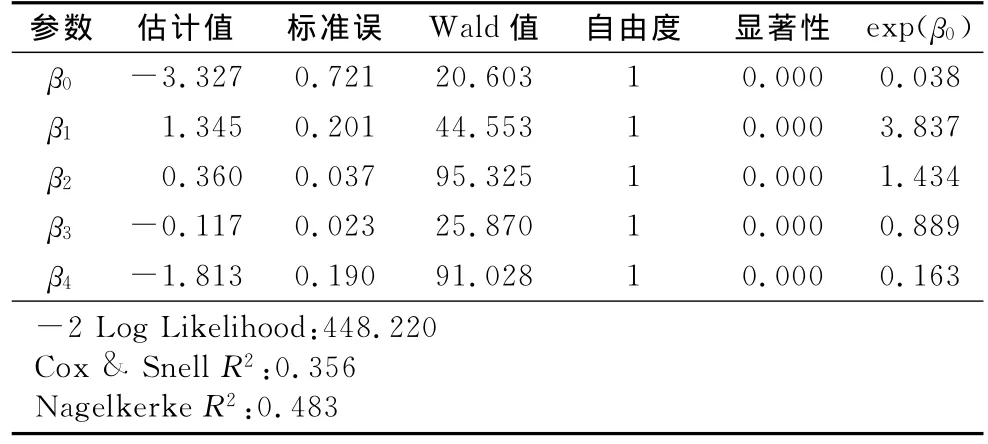
表3 普通Logistic回归模型参数估计结果Tab.3 Parameter estimation for Logistic model
对比表1和表3不难看出,普通Logistic模型与混合效应Logistic模型中固定效应参数估计值符号一致但绝对数值上相差较大.这说明两类模型反映的道面特征变量对状态转移概率的影响规律相同,同时多区域道面使用性能观测数据组内不可观测的异质性将导致总体平均模型参数估计出现一定的偏差,进而影响马尔可夫状态转移概率矩阵及其预测效果.总体而言,随机效应模型得到的参数估计,考虑了模型中自变量无法解释的不可观测的变异,更适合分析道面个体的性能状态变化特征.相对而言,混合效应模型中截距的负向增大导致道面状态转移的总体速率减小,但由于时间系数的增大,状态转移事件发生的时间区域将更为集中,速度更快.
分别采用表1和表3中固定效应估计值建立马尔可夫状态转移概率矩阵后,如已知道面使用性能的初始状态即可实现PCI状态等级(C)和PCI值的预测,公式如下:
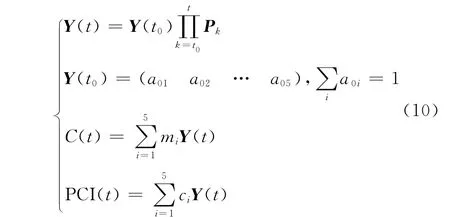
式中:Y(t0)为初始状态分布概率;Y(t)为预测状态分布概率;Pk为某时刻的状态转移概率矩阵;mi为状态等级i区间中值;ci为状态等级i区间中值.
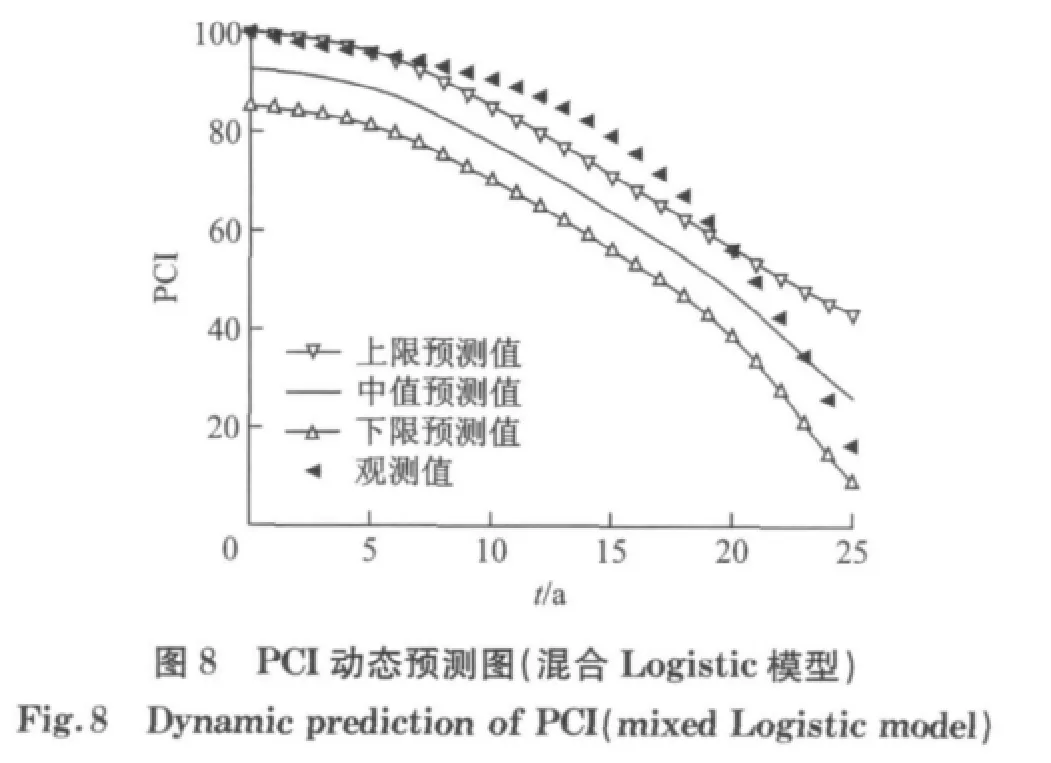
取初始状态向量Y(t0)=[1 0 0 0 0],应用式(10)分别计算得到对应道面状况指数PCI的确定型预测值和状态等级C.图7和图8分别为应用混合效应Logistic模型与普通Logistic模型得到道面状况指数PCI概率预测案例,由于道面状态等级为离散变量,图中分别绘制了ci取区间中值以及区间上、下限时的预测曲线.

图7 PCI动态预测图(普通Logistic模型)Fig.7 Dynamic prediction of PCI(Logistic model)
图8中部分PCI观测值超出了上限曲线范围,而图7中PCI观测值基本落在预测区间内,相比而言混合效应模型预测效果更佳.
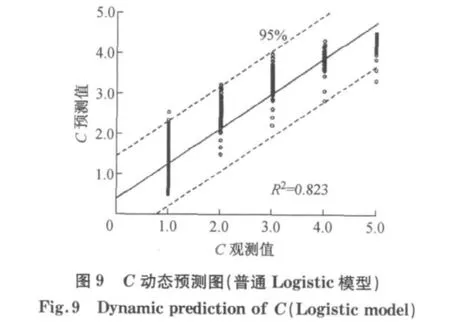
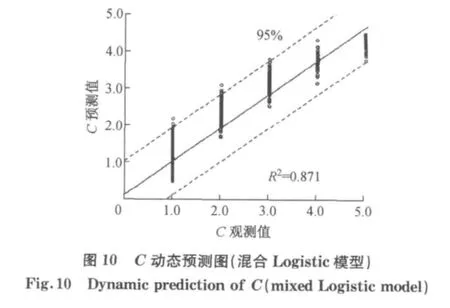
道面使用性能状态等级C观测值(横轴)与预测值(纵轴)对比情况结果如图9和图10所示.图中预测值与观测值之间具有良好的线性相关性,相关系数分别为0.823和0.871,同时混合效应模型得到的预测结果离散性较小.可见应用混合效应模型得到的道面使用性能马尔可夫概率拟合效果更优.
4 结论
本文讨论了应用广义线性混合效应模型建立马尔可夫过程中状态转移概率矩阵的方法和效果.通过以上分析,主要得到以下几点结论:
(1)混合效应Logistic模型能够建立道面厚度H、交通量logN、道面使用时间t及当前状态等级C等因素变量与道面性能状态转移概率之间的回归关系,获得非齐次马尔可夫转移概率矩阵,从而实现道面使用性能的动态概率预测.
(2)两类混合效应Logistic模型参数估计结果表明,模型中随机效应bi均具有统计学意义,说明道面个体数据之间存在不可观测的异质性.普通Logistic模型对此没有选择,直接将其视为总体误差,进而增大了残差相关性,影响参数估计的可靠性.由此可见,混合效应模型更适合多道面观测数据分析.
(3)普通Logistic回归模型和混合效应模型中固定效应参数估计值符号一致但绝对数值上相差较大.一方面说明两类模型反映的道面特征变量对状态转移概率的影响规律相同;另一方面进一步说明多区域道面使用性能观测数据组内不可观测的异质性将导致模型参数估计出现偏差,因此不容忽视.
(4)相比而言,采用混合效应Logistic模型建立的马尔可夫状态转移概率矩阵具有更好的拟合效果.PCI预测曲线与观测曲线较为接近,观测值基本落在预测区间内;道面状态等级(C)预测值和观测值相关系数由0.823提高到0.871.
[1] Shahin M Y.Pavement management for airports,roads,and parking lots[M].New York:Springer,2005.
[2] Ortiz-García J J,Costello S B,Snaith M S.Derivation of transition probability matrices for pavement deterioration modeling[J].Journal of Transportation Engineering,2006,132(2):141.
[3] Butt A A.Application of Markov process to pavement management systems at the network level[D].Urbana-Champaign:University of Illinois,1991.
[4] Madanat S,Mishalani R,Ibrahim W H W.Estimation of infrastructure transition probabilities from condition rating data[J].Journal of Infrastructure Systems,1995,1(2):120.
[5] Madanat S,Wan Ibrahim W H.Poisson regression models of infrastructure transition probabilities[J].Journal of Transportation Engineering,1995,121(3):267.
[6] Mishalani R G,Madanat S M.Computation of infrastructure transition probabilities using stochastic duration models[J].Journal of Infrastructure Systems,2002,8(4):139.
[7] Yang Jidong,Gunaratne M,Lu Jian John,et al.Use of recurrent Markov chains for modeling the crack performance of flexible pavements[J].Journal of Transportation Engineering,2005,131(11):861.
[8] LI Zheng.A probabilistic and adaptive approach to modeling performance of pavement infrastructure[D].Austin:University of Texas at Austin,2005.
[9] Chua K H,Monismith C L.Mechanistic model for transition probabilities[J].Journal of Transportation Engineering,1994,120(1):144.
[10] HONG Feng.Modeling heterogeneity in transportation infrastructure deterioration:application to pavement[D].Austin:University of Texas at Austin,2007.
[11] Hosmer D W,Lemeshow S.Applied Logistic regression[M].Hoboken:John Wiley &Sons,Inc,1989.
[12] Heagerty P J.Marginally specified Logistic-normal models for longitudinal binary data[J].Biometrics,1999,55(3):688.

